Dans l’article précédent (https://www.fmz.com/digest-topic/4187), nous avons présenté les stratégies de trading par paires et montré comment utiliser les données et l’analyse mathématique pour créer et automatiser des stratégies de trading.

La stratégie actions équilibrée long-short est une extension naturelle de la stratégie de trading par paires applicable à un panier d’objectifs de trading. Il est particulièrement adapté aux marchés commerciaux présentant de nombreuses variétés et interrelations, tels que le marché des devises numériques et le marché des contrats à terme sur matières premières.

Principes de base

La stratégie actions équilibrée long-short consiste à investir à la fois en position longue et en position courte sur un panier d’objectifs de trading. Tout comme le trading par paires, déterminez quelles cibles d’investissement sont bon marché et lesquelles sont chères. La différence est que la stratégie d’actions équilibrées long-short classera toutes les cibles d’investissement dans un pool de sélection d’actions pour déterminer quelles cibles d’investissement sont relativement bon marché. Ou chères. Il sera ensuite long sur les n premiers investissements en fonction du classement, et short sur les n derniers investissements avec un montant égal (valeur totale des positions longues = valeur totale des positions courtes).

Vous vous souvenez plus tôt quand nous avons dit que le trading de paires est une stratégie neutre sur le marché ? Il en va de même pour une stratégie actions équilibrée long-short, car le montant égal des positions longues et courtes garantit que la stratégie restera neutre sur le marché (non affectée par les fluctuations du marché). La stratégie est également statistiquement robuste ; en classant les investissements et en prenant plusieurs positions, vous pouvez exposer votre modèle de classement à de multiples expositions, plutôt qu’à une simple exposition au risque ponctuelle. Tout ce sur quoi vous pariez, c’est sur la qualité de votre système de classement.

Qu’est-ce qu’un système de classement ?

Un système de classement est un modèle qui attribue une priorité à chaque cible d’investissement en fonction de ses performances attendues. Les facteurs peuvent être des facteurs de valeur, des indicateurs techniques, des modèles de tarification ou une combinaison de tous les éléments ci-dessus. Par exemple, vous pouvez utiliser la mesure du momentum pour classer une liste d’investissements qui suivent la tendance : les investissements avec le momentum le plus élevé devraient continuer à bien performer et recevoir les classements les plus élevés ; les investissements avec le moins de momentum seraient les moins performants et ont les rendements les plus faibles.

Le succès de cette stratégie dépend presque entièrement du système de classement utilisé, c’est-à-dire que votre système de classement est capable de séparer les investissements très performants des investissements peu performants, réalisant ainsi mieux les rendements de la stratégie cible d’investissement long-short. Il est donc très important de développer un système de classement.

Comment formuler un plan de classement ?

Une fois que nous avons mis en place un système de classement, nous voulons évidemment pouvoir en tirer profit. Nous y parvenons en investissant le même montant d’argent pour acheter les investissements les mieux classés et vendre à découvert les investissements les moins bien classés. Cela garantit que la stratégie ne gagnera de l’argent qu’en proportion de la qualité de ses classements et sera « neutre sur le marché ».

Supposons que vous classiez tous les investissements m, que vous ayez n dollars à investir et que vous souhaitiez détenir un total de 2p (où m> 2p) positions. Si l’on s’attend à ce que l’investissement de rang 1 soit le moins performant, alors l’investissement de rang m devrait être le plus performant :

• Vous organisez les objectifs d’investissement comme suit : 1, …, p et short 2/2p USD objectifs d’investissement

• Vous organisez les objectifs d’investissement comme suit : m-p,……,m, et optez pour une position longue sur n/2p dollars d’objectifs d’investissement

Avis:Étant donné que le prix d’un objectif d’investissement en raison de sauts de prix ne divisera pas toujours n/2p de manière égale, et que certains objectifs d’investissement doivent être achetés en nombres entiers, il y aura des algorithmes inexacts, et l’algorithme doit être aussi proche que possible de ce nombre. Pour la stratégie exécutée avec n = 100 000 et p = 500, nous voyons :

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

Cela peut entraîner de gros problèmes pour les prix avec des fractions supérieures à 100 (comme les marchés à terme sur matières premières), car vous ne pouvez pas ouvrir de positions avec des prix fractionnaires (ce problème n’existe pas sur le marché des crypto-monnaies). Nous atténuons ce problème en réduisant les transactions à prix fractionnés ou en augmentant le capital.

Prenons un exemple hypothétique.

• Construire notre environnement de recherche sur la plateforme quantitative Inventor

Tout d’abord, pour que le travail soit fluide, nous devons créer notre environnement de recherche. Dans cet article, nous utilisons la plateforme quantitative Inventor (FMZ.COM) pour créer l’environnement de recherche, principalement pour pouvoir utiliser l’API pratique et rapide interface et encapsulation de cette plateforme ultérieurement. Système Docker complet.

Dans le nom officiel de la plateforme quantitative Inventor, ce système Docker est appelé système hôte.

Pour plus d’informations sur la manière de déployer des hôtes et des robots, veuillez vous référer à mon article précédent : https://www.fmz.com/bbs-topic/4140

Les lecteurs qui souhaitent acheter leur propre hébergeur de déploiement de serveur de cloud computing peuvent se référer à cet article : https://www.fmz.com/bbs-topic/2848

Après avoir déployé avec succès le service de cloud computing et le système hôte, nous installerons l’outil Python le plus puissant : Anaconda

Afin d’obtenir tous les environnements de programme pertinents requis pour cet article (bibliothèques dépendantes, gestion des versions, etc.), le moyen le plus simple est d’utiliser Anaconda. Il s’agit d’un écosystème de science des données Python packagé et d’un gestionnaire de dépendances.

Pour la méthode d’installation d’Anaconda, veuillez vous référer au guide officiel d’Anaconda : https://www.anaconda.com/distribution/

Cet article utilisera également numpy et pandas, deux bibliothèques très populaires et importantes dans le calcul scientifique Python.

Pour le travail de base ci-dessus, vous pouvez également vous référer à mon article précédent, qui présente comment configurer l’environnement Anaconda et les deux bibliothèques numpy et pandas. Pour plus de détails, veuillez consulter : https://www.fmz.com/digest- sujet/4169

Nous générons des investissements aléatoires et des facteurs aléatoires et les classons. Supposons que nos rendements futurs dépendent réellement de ces valeurs factorielles.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

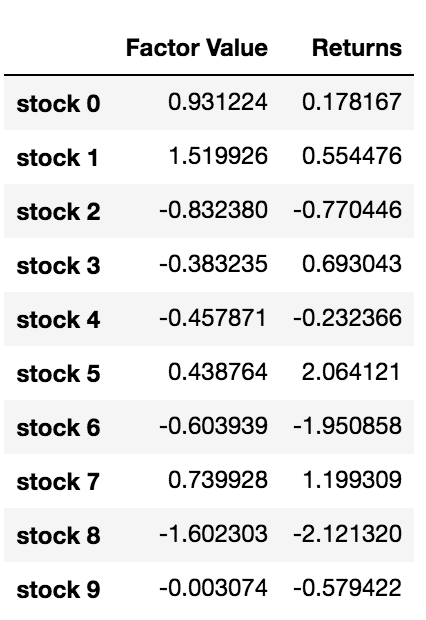
Maintenant que nous avons les valeurs des facteurs et les rendements, nous pouvons voir ce qui se passe si nous classons les investissements en fonction des valeurs des facteurs, puis ouvrons des positions longues et courtes.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

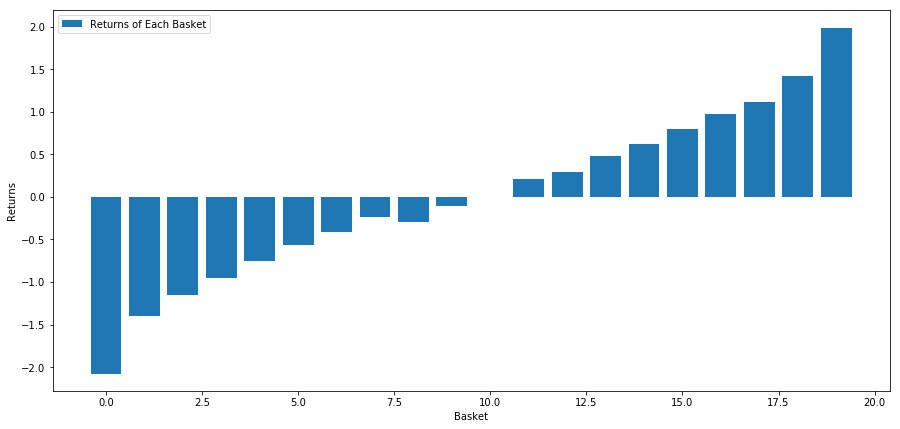
Notre stratégie consiste à investir à la hausse sur le premier investissement classé dans un panier d’objectifs d’investissement et à la baisse sur le dixième objectif d’investissement classé. Les avantages de cette stratégie sont les suivants :

basket_returns[number_of_baskets-1] - basket_returns[0]

Le résultat est: 4.172

Misez sur notre modèle de classement pour séparer les investissements performants de ceux peu performants.

Dans la suite de cet article, nous discutons de la manière d’évaluer les systèmes de classement. L’avantage de gagner de l’argent grâce à l’arbitrage basé sur le classement est qu’il n’est pas affecté par les désordres du marché, mais peut au contraire en tirer parti.

Prenons un exemple concret.

Nous chargeons les données de 32 actions de différents secteurs du S&P 500 et essayons de les classer.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Utilisons l’indicateur de momentum normalisé sur une période d’un mois comme base de classement

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Nous allons maintenant analyser le comportement de notre action et voir comment notre action se comporte sur le marché en fonction des facteurs de classement que nous avons choisis.

Analyser les données

Comportement des stocks

Voyons comment notre panier d’actions sélectionné se comporte dans notre modèle de classement. Pour ce faire, calculons les rendements prévisionnels sur une semaine pour toutes les actions. Nous pouvons ensuite examiner la corrélation entre le rendement prévisionnel sur une semaine de chaque action et la dynamique des 30 jours précédents. Les actions qui affichent une corrélation positive suivent la tendance, tandis que les actions qui affichent une corrélation négative reviennent à la moyenne.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

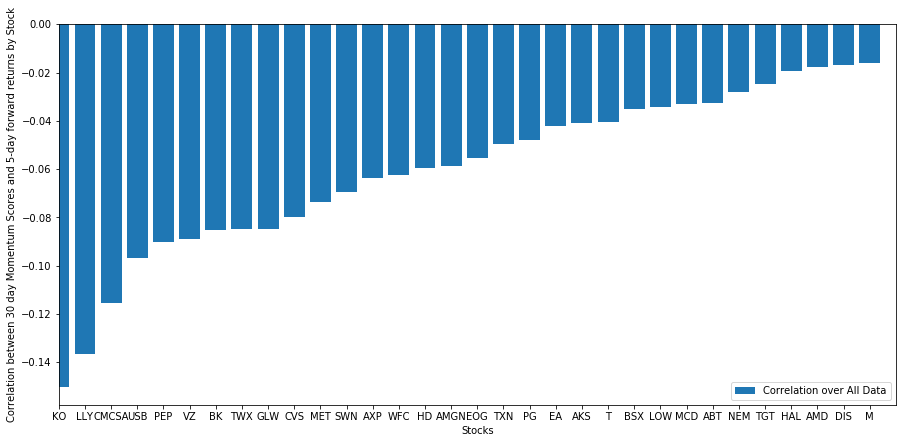
Tous nos stocks sont voués à revenir dans une certaine mesure ! (Apparemment, notre univers choisi fonctionne de cette façon). Cela nous indique que si une action est bien classée dans l’analyse du momentum, nous devons nous attendre à ce qu’elle sous-performe la semaine prochaine.

Corrélation entre le classement Momentum Score et les rendements

Ensuite, nous devons examiner la corrélation entre notre score de classement et les rendements futurs globaux du marché, c’est-à-dire la relation entre la prévision des rendements attendus et nos facteurs de classement. Des niveaux de corrélation plus élevés peuvent-ils prédire des rendements relatifs plus faibles, ou vice versa ?

Pour ce faire, nous calculons la corrélation quotidienne entre le momentum sur 30 jours et les rendements futurs sur 1 semaine pour toutes les actions.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

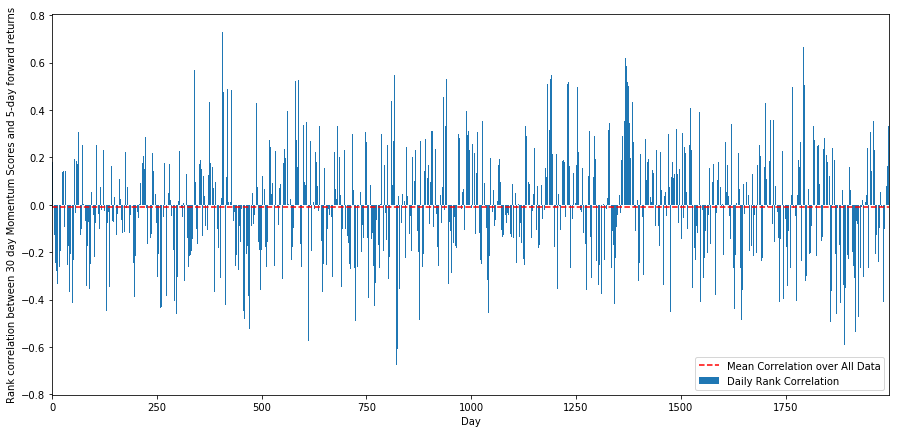
La corrélation journalière est assez bruyante, mais très légère (ce qui est attendu puisque nous avons dit que tous les stocks signifieraient un retour en arrière). Nous examinons également la corrélation mensuelle moyenne des rendements prévisionnels sur 1 mois.

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

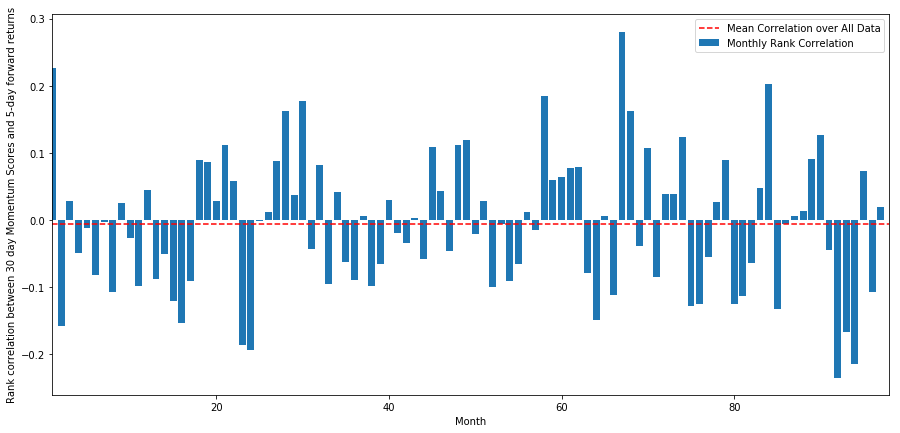
Nous pouvons voir que la corrélation moyenne est à nouveau légèrement négative, mais varie également beaucoup d’un mois à l’autre.

Rendement moyen du panier d’actions

Nous avons calculé les rendements d’un panier d’actions tirées de notre classement. Si nous classons toutes les actions et les divisons ensuite en n groupes, quel sera le rendement moyen de chaque groupe ?

La première étape consiste à créer une fonction qui donnera le rendement moyen et le facteur de classement pour chaque panier donné chaque mois.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Nous calculons le rendement moyen de chaque panier lors du classement des actions en fonction de ce score. Cela devrait nous donner une bonne idée de leur relation sur une longue période de temps.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

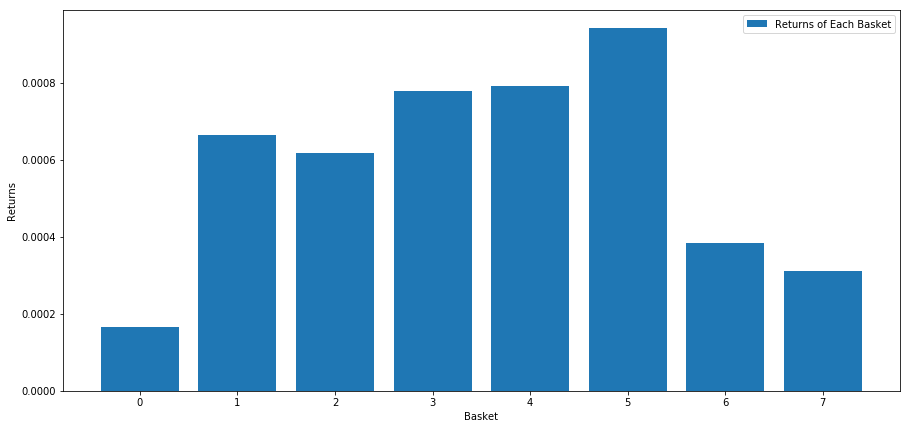
Il semble que nous soyons capables de distinguer les plus performants des moins performants.

Cohérence de l’étalement (base)

Bien sûr, ce ne sont que des relations moyennes. Afin de comprendre dans quelle mesure la relation est cohérente et si nous sommes prêts à conclure un accord, nous devons changer notre approche et notre attitude à son égard au fil du temps. Ensuite, nous examinerons leurs spreads mensuels (base) pour les deux années précédentes. Nous pouvons voir plus de changements et effectuer des analyses plus approfondies pour déterminer si ce score de momentum est négociable.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

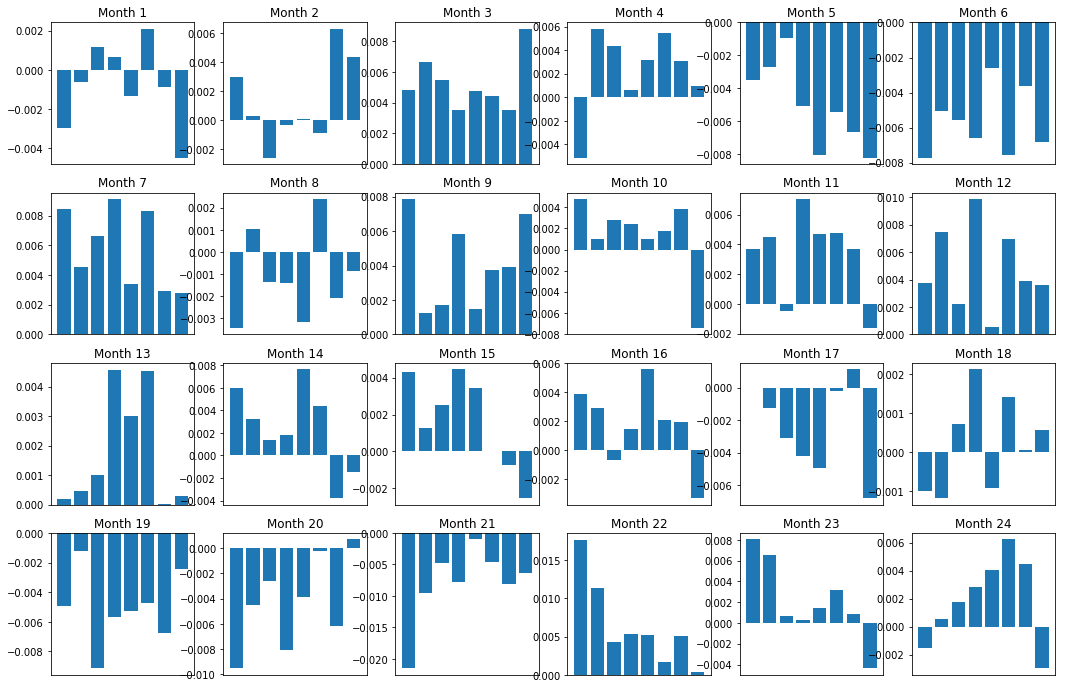
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

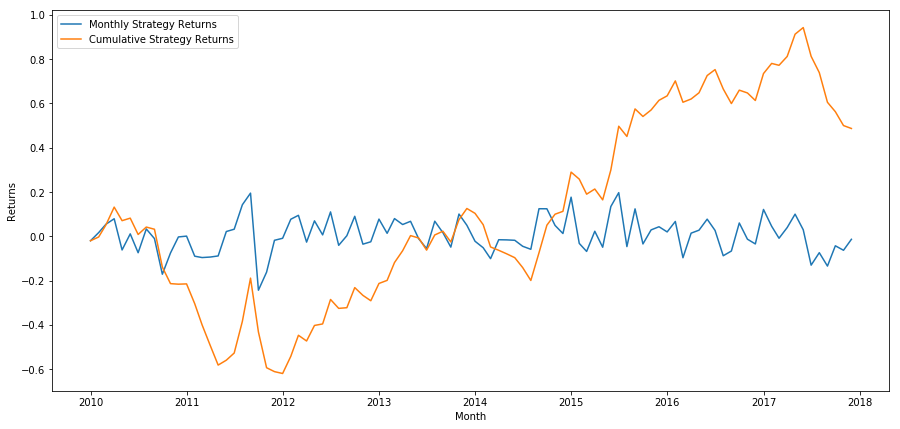
Enfin, examinons les rendements si nous étions longs sur le dernier panier et short sur le premier panier chaque mois (en supposant une répartition égale du capital entre chaque titre).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Rendement annuel : 5,03 %

Nous constatons que nous avons un système de classement très faible qui ne distingue que modestement les actions à haute performance des actions à faible performance. De plus, ce système de classement manque de cohérence et varie considérablement d’un mois à l’autre.

Trouver le bon système de classement

Pour mettre en œuvre une stratégie d’actions équilibrée long-short, il vous suffit en réalité de déterminer le système de classement. Tout ce qui suit est mécanique. Une fois que vous avez une stratégie d’actions équilibrée long-short, vous pouvez échanger différents facteurs de classement sans changer grand-chose d’autre. C’est un moyen très pratique d’itérer rapidement sur vos idées sans avoir à vous soucier de modifier l’intégralité du code à chaque fois.

Le système de classement peut également provenir de presque n’importe quel modèle. Il n’est pas nécessaire qu’il s’agisse d’un modèle factoriel basé sur la valeur, il peut s’agir d’une technique d’apprentissage automatique qui prédit les rendements un mois à l’avance et les classe en fonction de cela.

Sélection et évaluation des systèmes de classement

Le système de classement constitue l’avantage de la stratégie actions équilibrée long-short et constitue également son élément le plus important. Choisir un bon système de classement est un projet systématique et il n’existe pas de réponses simples.

Un bon point de départ est de choisir des technologies existantes connues et de voir si vous pouvez les modifier légèrement pour obtenir des rendements plus élevés. Nous allons discuter ici de quelques points de départ :

• Cloner et ajuster:Choisissez quelque chose qui est souvent discuté et voyez si vous pouvez le modifier légèrement à votre avantage. En règle générale, les facteurs publics n’auront plus de signaux de trading car ils ont été entièrement arbitrés hors du marché. Cependant, ils peuvent parfois vous orienter dans la bonne direction.

• Modèle de tarification:Tout modèle qui prédit les rendements futurs peut être un facteur et a le potentiel d’être utilisé pour classer votre panier d’objectifs de trading. Vous pouvez prendre n’importe quel modèle de tarification complexe et le convertir en un système de classement.

• Facteurs basés sur les prix (indicateurs techniques):Les facteurs basés sur les prix, comme ceux dont nous avons parlé aujourd’hui, prennent des informations sur le prix historique de chaque action et les utilisent pour générer une valeur de facteur. Les exemples peuvent être des indicateurs de moyenne mobile, des indicateurs de momentum ou des indicateurs de volatilité.

• Régression et dynamique:Il convient de noter que certains facteurs estiment qu’une fois que les prix évoluent dans une direction, ils continueront à le faire. Certains facteurs sont tout à fait à l’opposé. Les deux sont des modèles valables sur des périodes et des actifs différents, et il est important d’étudier si le comportement sous-jacent est basé sur la dynamique ou la régression.

• Facteurs fondamentaux (basés sur la valeur):Il s’agit d’utiliser une combinaison de valeurs fondamentales comme le PE, les dividendes, etc. La valeur fondamentale contient des informations liées à des faits réels concernant une entreprise et peut donc être plus puissante que le prix à bien des égards.

En fin de compte, développer des prédicteurs est une course aux armements dans laquelle il faut essayer de garder une longueur d’avance. Les facteurs sont arbitrés hors du marché et ont une durée de vie, vous devez donc continuellement travailler pour déterminer dans quelle mesure vos facteurs ont subi une dégradation et quels nouveaux facteurs peuvent être utilisés pour les remplacer.

Autres considérations

• Rééquilibrage de fréquence

Chaque système de classement prédit les rendements sur une période de temps légèrement différente. Le retour à la moyenne basé sur les prix pourrait être prédictif sur quelques jours, tandis que les modèles de facteurs basés sur la valeur pourraient être prédictifs sur quelques mois. Il est très important de déterminer l’horizon temporel que le modèle doit prévoir et de le valider statistiquement avant d’exécuter la stratégie. Vous ne voulez certainement pas sur-adapter en essayant d’optimiser votre fréquence de rééquilibrage ; vous en trouverez inévitablement une qui surpasse aléatoirement les autres. Une fois que vous avez déterminé l’horizon temporel prévu par votre système de classement, essayez de rééquilibrer à peu près à cette fréquence afin de Tirez le meilleur parti de votre modèle.

• Capacité du capital et coûts de transaction

Chaque stratégie a une exigence de capital minimum et maximum, le seuil minimum étant généralement déterminé par les coûts de transaction.

Négocier trop d’actions entraînera des coûts de transaction élevés. En supposant que vous souhaitiez acheter 1 000 actions, chaque rééquilibrage entraînera des coûts de plusieurs milliers de dollars. Votre base de capital doit être suffisamment élevée pour que les coûts de transaction ne représentent qu’une petite fraction des rendements générés par votre stratégie. Par exemple, si votre capital est de 100 000 \( et que votre stratégie rapporte 1 % (1 000 \)) par mois, la totalité de ce rendement sera absorbée par les coûts de transaction. Vous auriez besoin de millions de dollars de capital pour exécuter cette stratégie afin de réaliser un profit sur plus de 1 000 actions.

Le seuil d’actifs minimum dépend principalement du nombre d’actions négociées. Cependant, la capacité maximale est également très élevée et les stratégies d’actions équilibrées long-short sont capables de négocier des centaines de millions de dollars sans perdre leur avantage. C’est vrai parce que la stratégie est rééquilibrée relativement rarement. Le montant total des actifs divisé par le nombre d’actions négociées donnera une valeur en dollars très faible par action, et vous n’avez pas à vous soucier de l’influence de votre volume de transactions sur le marché. Disons que vous négociez 1 000 actions, cela représente 100 000 000 \(. Si vous rééquilibriez l’intégralité de votre portefeuille chaque mois, vous ne négocieriez que 100 000 \) par mois par action, ce qui n’est pas suffisant pour constituer une part de marché significative pour la plupart des titres.