तंत्रिका नेटवर्क और डिजिटल मुद्रा मात्रात्मक व्यापार श्रृंखला (1) - एलएसटीएम बिटकॉइन मूल्य की भविष्यवाणी करता है

तंत्रिका नेटवर्क और डिजिटल मुद्रा मात्रात्मक व्यापार श्रृंखला (1) - एलएसटीएम बिटकॉइन मूल्य की भविष्यवाणी करता है

1. संक्षिप्त परिचय

डीप न्यूरल नेटवर्क हाल के वर्षों में अधिक से अधिक लोकप्रिय हो गया है। इसने कई क्षेत्रों में अतीत में हल नहीं की जा सकने वाली समस्याओं को हल किया है और अपनी मजबूत क्षमता का प्रदर्शन किया है। समय श्रृंखलाओं की भविष्यवाणी में, आमतौर पर उपयोग किए जाने वाले न्यूरल नेटवर्क की कीमत आरएनएन है, क्योंकि इसमें न केवल वर्तमान डेटा इनपुट है, बल्कि ऐतिहासिक डेटा इनपुट भी है। बेशक, जब हम आरएनएन मूल्य भविष्यवाणी के बारे में बात करते हैं, तो हम अक्सर आरएनएन में से एक के बारे में बात करते हैंः एलएसटीएम। यह पेपर पाइटॉर्च के आधार पर बिटकॉइन की कीमत की भविष्यवाणी करने के लिए एक मॉडल का निर्माण करेगा। हालांकि इंटरनेट पर बहुत सारी प्रासंगिक जानकारी है, लेकिन यह अभी भी पर्याप्त रूप से गहन नहीं है, और अपेक्षाकृत कम लोग हैं जो पाइटॉर्च का उपयोग करते हैं। अभी भी एक लेख लिखना आवश्यक है। अंतिम परिणाम बिटकॉइन की अगली शुरुआती कीमत, समापन मूल्य, उच्चतम व्यापार मूल्य, सबसे कम मूल्य और मात्रा का उपयोग करना है। मेरा व्यक्तिगत ज्ञान और आलोचनाओं के लिए मेरी आशा है कि न्यूरल नेटवर्क की अगली कीमत का अनुमान लगाना सीमित है। यह ट्यूटोरियल FMZ क्वांट ट्रेडिंग प्लेटफॉर्म द्वारा तैयार किया गया है (www.fmz.com) संपर्क के लिए क्यूक्यू समूह में शामिल होने के लिए आपका स्वागत है: 863946592।

2. डेटा और संदर्भ

एफएमजेड क्वांट ट्रेडिंग प्लेटफॉर्म से प्राप्त बिटकॉइन मूल्य डेटाःhttps://www.quantinfo.com/Tools/View/4.html. मूल्य पूर्वानुमान का एक संबंधित उदाहरणःhttps://yq.aliyun.com/articles/538484. आरएनएन मॉडल का विस्तृत परिचयःhttps://zhuanlan.zhihu.com/p/27485750. आरएनएन के इनपुट और आउटपुट को समझनाःhttps://www.zhihu.com/question/41949741/answer/318771336. पिटॉर्च के बारे में: आधिकारिक दस्तावेज:https://pytorch.org/docsअन्य जानकारी के लिए आप स्वयं खोज कर सकते हैं। इसके अतिरिक्त, आपको इस लेख को पढ़ने के लिए कुछ पूर्व ज्ञान की आवश्यकता है, जैसे कि पांडा / पायथन / डेटा प्रसंस्करण, लेकिन इससे कोई फर्क नहीं पड़ता कि आप नहीं करते हैं।

3. पिटॉर्च एलएसटीएम मॉडल के पैरामीटर

एलएसटीएम के पैरामीटर:

जब मैंने पहली बार दस्तावेज पर इन घने मापदंडों को देखा, मेरी प्रतिक्रिया थी: यह क्या है?

जैसे-जैसे मैं धीरे-धीरे पढ़ता गया, मैं अंततः समझ गया।

input_size: वेक्टर x का विशेषता आकार इनपुट करें. यदि समापन मूल्य समापन मूल्य द्वारा भविष्यवाणी की जाती है, तो input_size=1; यदि समापन मूल्य उच्च उद्घाटन और निम्न समापन द्वारा भविष्यवाणी की जाती है, तो input_size=4.hidden_size: निहित परत का आकारnum_layers: आरएनएन की परतों की संख्या।batch_first: यदि सही है, तो पहला इनपुट आयाम batch_size है, जो भी बहुत भ्रमित करने वाला है, और इसे नीचे विस्तार से वर्णित किया जाएगा।

डेटा पैरामीटर दर्ज करेंः

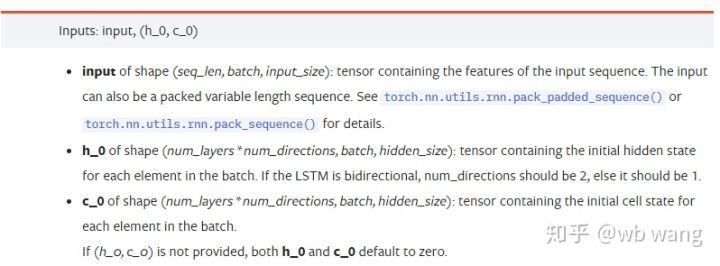
input: विशिष्ट इनपुट डेटा एक त्रि-आयामी टेंसर है, और विशिष्ट आकार हैः (seq_len, बैच, इनपुट_साइज़). जहां, seq_len अनुक्रम की लंबाई को संदर्भित करता है, अर्थात, ऐतिहासिक डेटा पर विचार करने के लिए LSTM को कितना समय चाहिए। ध्यान दें कि यह केवल डेटा के प्रारूप को संदर्भित करता है, LSTM की आंतरिक संरचना नहीं। एक ही LSTM मॉडल विभिन्न seqs_lens डेटा दर्ज कर सकता है, जो भविष्यवाणी परिणाम दे सकता है; बैच बैच के आकार को संदर्भित करता है, जो डेटा के कितने विभिन्न समूहों का प्रतिनिधित्व करता है; input_size पिछले इनपुट_साइज है।h_0: प्रारंभिक छिपी हुई स्थिति, आकार के रूप में (num_layers * num_directions, बैच, hidden_size), यदि यह एक दो-तरफा नेटवर्क है, num_directions=2.c_0: सेल की प्रारंभिक अवस्था, ऊपर के रूप में आकार, निर्दिष्ट नहीं किया जा सकता है।

आउटपुट पैरामीटरः

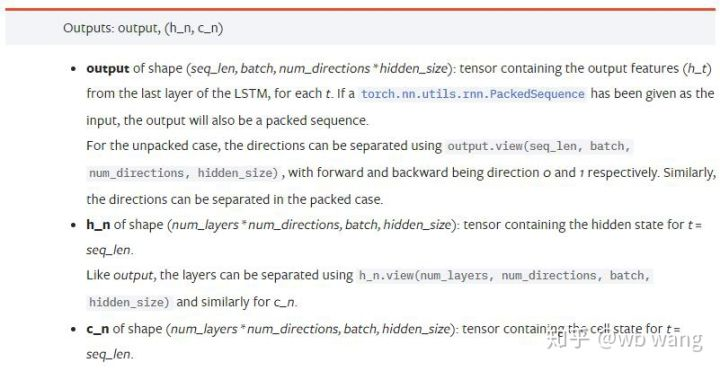
output: आउटपुट का आकार (seq_len, बैच, num_directions * hidden_size), ध्यान दें कि यह मॉडल पैरामीटर batch_first से संबंधित है.h_n: t = seq_len के क्षण में h अवस्था, h_0 के समान आकार।c_n: t = seq_len के क्षण में c अवस्था, c_0 के समान आकार।

4. LSTM इनपुट और आउटपुट का एक सरल उदाहरण

पहले आवश्यक पैकेज आयात करें

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

एलएसटीएम मॉडल को परिभाषित करें

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

इनपुट डेटा तैयार करें

x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

x का आकार (3,4,5) है, क्योंकि हमने परिभाषित किया हैbatch_first=Trueपहले, इस समय बैच_साइज़ का आकार 3, sqe_len 4, input_size 5 है। X [0] पहले बैच का प्रतिनिधित्व करता है।

यदि batch_first परिभाषित नहीं है, तो डिफ़ॉल्ट मान False है, तो इस समय डेटा प्रतिनिधित्व पूरी तरह से अलग है। बैच का आकार 4, sqe_len है 3, input_size है 5. इस समय, x [0] t = 0 पर सभी बैचों के डेटा का प्रतिनिधित्व करता है, और इसी तरह। मुझे लगता है कि यह सेटिंग सहज नहीं है, इसलिए मैंने पैरामीटर जोड़ा हैbatch_first=True.

दोनों के बीच डेटा रूपांतरण भी बहुत सुविधाजनक हैःx.permute (1,0,2)

इनपुट और आउटपुट

एलएसटीएम के इनपुट और आउटपुट का आकार बहुत भ्रमित करने वाला है, और निम्नलिखित चित्र हमें समझने में मदद कर सकता हैः

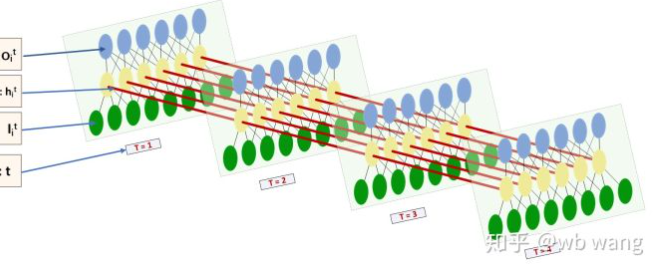
सेःhttps://www.zhihu.com/question/41949741/answer/318771336.

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

आउटपुट परिणाम का अवलोकन करें, जो पिछले पैरामीटर व्याख्या के अनुरूप है. ध्यान दें कि hn.size() का दूसरा मान 3 है, जो batch_size के आकार के अनुरूप है, जिसका अर्थ है कि मध्यवर्ती स्थिति hn में सहेजी नहीं जाती है, केवल अंतिम चरण सहेजा जाता है. चूंकि हमारे LSTM नेटवर्क में दो परतें हैं, वास्तव में hn की अंतिम परत का आउटपुट आउटपुट का मूल्य है। आउटपुट का आकार [3, 4, 10] है, जो t = 0,1,2,3 के सभी समय में परिणामों को बचाता है, इसलिएः

hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. बिटकॉइन बाजार के आंकड़े तैयार करें

बहुत कुछ पहले कहा गया है, जो कि केवल एक प्रस्तावना है। एलएसटीएम के इनपुट और आउटपुट को समझना बहुत महत्वपूर्ण है। अन्यथा, इंटरनेट से यादृच्छिक रूप से कुछ कोड निकालने से गलतियां करना आसान है। समय श्रृंखला में एलएसटीएम की मजबूत क्षमता के कारण, भले ही मॉडल गलत हो, अंत में अच्छे परिणाम प्राप्त किए जा सकते हैं।

डेटा अधिग्रहण

Bitfinex Exchange में BTC_USD ट्रेडिंग जोड़ी के बाजार डेटा का प्रयोग किया जाता है।

import requests
import json

resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

डेटा प्रारूप इस प्रकार है:

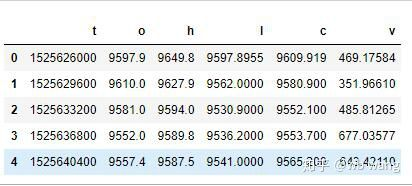
डाटा प्रीप्रोसेसिंग

df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.

डेटा मानकीकरण की विधि बहुत मोटी है, और कुछ समस्याएं होंगी. सिर्फ प्रदर्शन के लिए, आप डेटा मानकीकरण का उपयोग कर सकते हैं जैसे कि वापसी दरें.

प्रशिक्षण डेटा तैयार करें

seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

train_x और train_y के अंतिम आकार हैंः torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). चूंकि हमारा मॉडल 10 अवधि के डेटा के आधार पर अगली अवधि की समापन कीमत की भविष्यवाणी करता है, इसलिए सिद्धांत रूप में 800 बैच हैं, जब तक कि 800 पूर्वानुमानित समापन मूल्य हैं। लेकिन प्रत्येक बैच में train_y में 10 डेटा हैं। वास्तव में, प्रत्येक बैच भविष्यवाणी का मध्यवर्ती परिणाम आरक्षित है। अंतिम हानि की गणना करते समय, सभी 10 भविष्यवाणी परिणामों को ध्यान में रखा जा सकता है और train_y में वास्तविक मूल्य की तुलना की जा सकती है। सैद्धांतिक रूप से, हम केवल अंतिम भविष्यवाणी परिणाम के नुकसान की गणना कर सकते हैं। क्योंकि LSTM मॉडल में वास्तव में seq_lenful पैरामीटर नहीं है, इसलिए मॉडल को विभिन्न लंबाई पर लागू किया जा सकता है, और मध्य में भविष्यवाणी के परिणाम भी सार्थक हैं, इसलिए मैं संयोजन और गणना करना पसंद करता हूं।

ध्यान दें कि प्रशिक्षण डेटा तैयार करते समय, खिड़की का आंदोलन कूदता है, और पहले से ही उपयोग किए गए डेटा का उपयोग नहीं किया जाता है। बेशक, खिड़की को एक-एक करके भी स्थानांतरित किया जा सकता है, ताकि प्राप्त प्रशिक्षण सेट बहुत बड़ा हो। हालांकि, मुझे लगा कि आसन्न बैच डेटा बहुत दोहराव था, इसलिए मैंने वर्तमान विधि को अपनाया।

6. LSTM मॉडल का निर्माण करें

अंतिम मॉडल का निर्माण निम्नानुसार किया गया है जिसमें दो-परत LSTM और एक रैखिक परत शामिल है।

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.

    def forward(self, x):
        x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.

7. मॉडल को प्रशिक्षित करना शुरू करें

अंत में हम प्रशिक्षण शुरू करते हैं, कोड इस प्रकार हैः

criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
    out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # Reverse propagation losses
    optimizer.step() # Update parameters
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

प्रशिक्षण के परिणाम इस प्रकार हैं:

8. मॉडल मूल्यांकन

मॉडल का अनुमानित मूल्यः

p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

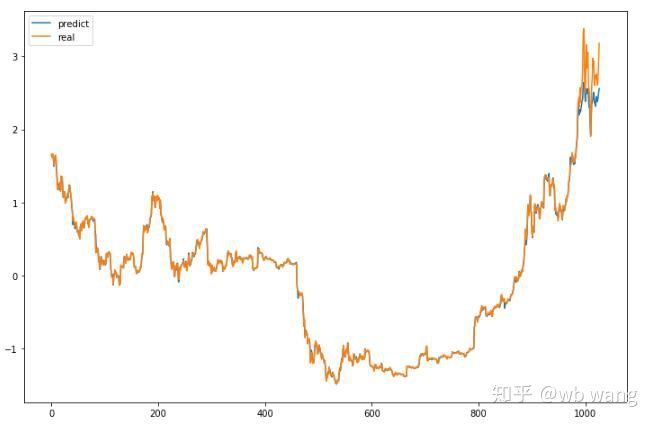
यह चार्ट से देखा जा सकता है कि प्रशिक्षण डेटा (800 से पहले) बहुत सुसंगत हैं, लेकिन बाद की अवधि में बिटकॉइन की कीमत बढ़ी है। मॉडल ने इन डेटा को नहीं देखा है, इसलिए भविष्यवाणी अपर्याप्त है। इससे यह भी पता चलता है कि डेटा के मानकीकरण में समस्याएं हैं। यद्यपि पूर्वानुमानित मूल्य सटीक नहीं हो सकता है, लेकिन बढ़ते और घटते मूल्य की भविष्यवाणी की सटीकता क्या है?

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

नतीजतन, वृद्धि और गिरावट का पूर्वानुमान करने की सटीकता दर 81.4% तक पहुंच गई, जो अभी भी मेरी अपेक्षाओं से अधिक है। मुझे नहीं पता कि क्या कुछ गलत है।

बेशक, यह मॉडल वास्तविक बॉट पर लागू नहीं है, लेकिन यह सरल और समझने में आसान है। बस इसके साथ शुरू करो। अगला, डिजिटल मुद्रा मात्रात्मककरण में तंत्रिका नेटवर्क अनुप्रयोग के अधिक परिचयात्मक पाठ्यक्रम होंगे।