機械学習の8大アルゴリズム比較

作者: リン・ハーン発明者量化 - 微かな夢作成日:2016年12月05日 10:42:02 更新日:

機械学習の8大アルゴリズム比較

この記事では,以下のような一般的なアルゴリズムの適応シナリオとそのメリットとデメリットについて詳しく説明します.

機械学習アルゴリズムは,分類,回帰,分類,推薦,画像認識などの領域で,非常に多く,適切なアルゴリズムを見つけることは本当に簡単ではありません.

一般的には,SVM,GBDT,Adaboostなどの一般的なアルゴリズムを最初に選択します. 現在,ディープラーニングは熱中しており,神経ネットワークも良い選択肢です.

精度 (accuracy) を気にするなら,最も良い方法は,各アルゴリズムを1つずつテストし,比較し,パラメータを調整して,それぞれのアルゴリズムが最適であることを確認し,最後に最良のものを選択することです.

しかし,もしあなたがあなたの問題を解決するのに十分なアルゴリズムを探しているだけなら,または参考になるいくつかのヒントがあるなら,下記のアルゴリズムのメリットとデメリットを分析し,メリットとデメリットをベースに,それを選ぶのが簡単です.

## 偏差と偏差統計学では,モデルが良いか悪いかは,偏差と差によって測定されるので,まずは偏差と差を普及させましょう.

偏差:予測値 (推定値) の期待値Eと実際の値Yの差を記述する.偏差が大きいほど,実際のデータから離れている.

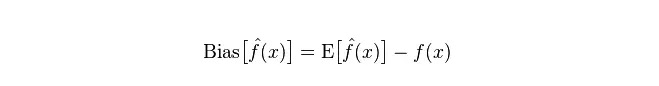
机器学习8大算法比较

差分:予測値Pの変化範囲,分散度,予測値の差分,つまり期待値Eからの距離を記述する.差分が大きいほど,データの分布が分散する.

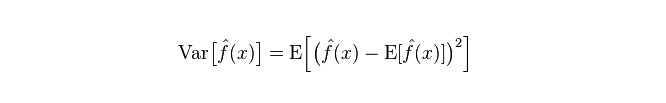
机器学习8大算法比较

モデルにおける実際の誤差は,次の図のように両者の合計である.

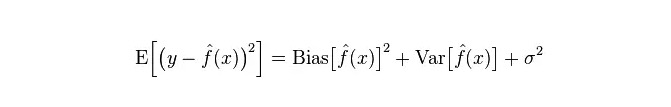
机器学习8大算法比较

小型のトレーニングセットの場合,低偏差/高偏差分別器 (例えば,朴素なベイエスNB) は,低偏差/高偏差分別器 (例えば,KNN) よりも優れている.

しかし,あなたのトレーニングセットが大きくなるにつれて,モデルが元のデータに対する予測能力が向上するにつれて,偏差は減少し,低偏差/高偏差分類器が徐々に優位性を発揮する (低偏差があるため),高偏差分類器が正確なモデルを提供するのに不十分になる.

もちろん,これは生成モデル (NB) と判断モデル (KNN) の違いと考えることもできます.

## なぜ素朴なベアスは偏差値が低いのか?

この記事へのトラックバック一覧です.

まず,トレーニングセットとテストセットの関係を知ると仮定します. 簡単に言えば,テストセットでモデルを学習し,テストセットを入手して使用すると,テストセットの誤差率に基づいて評価されます.

しかし,多くの場合,テストセットとトレーニングセットは同じデータ分布に一致していると仮定するだけで,実際のテストデータを得ることはできません. では,テストエラー率を測定するには,トレーニングエラー率だけを見てみましょう.

訓練サンプルが少ない (少なくとも十分ではない) のため,訓練セットから得られたモデルは常に正しくない. 訓練セットで100%の正確さがあるとしても,それが真のデータ分布を描いているとは言えない. 真のデータ分布を描くのが我々の目的であり,訓練セットの限られたデータ点だけを描くのではないことを知るべきである.

また,実際,訓練サンプルにはしばしばノイズエラーがあるため,訓練集合の完璧を目指しすぎると,非常に複雑なモデルを使用すると,モデルが訓練集合内の誤差をすべて真のデータ分布特征として捉え,誤ったデータ分布推定を得ることになる.

この状態では,実際のテストセットでは誤りがある (この現象は適合性と呼ばれる).しかし,単純すぎないモデルではできません.そうでなければ,データ分布が比較的複雑であるときに,モデルがデータ分布を描写するのに不十分である (訓練セットでも誤り率が高いことが示されています.この現象は不適合性です).

超適合表示は,モデルが実際のデータ分布よりも複雑であることを示し,非適合表示は,モデルが実際のデータ分布よりも単純であることを示します.

統計学的な学習の枠組みの中で,モデル複雑性を描くとき,Error = Bias + Variance という考えがあります.ここで,Error はおそらくモデルの予測誤差率として理解され,二つの部分で構成されています.

したがって,これは単純なベイエスの分析を容易にする. 単純なベイエスは,各データが無関係であると仮定し,著しく簡素化されたモデルである. したがって,このような単純なモデルでは,ほとんどの場合,バイアスの部分はバリエンス部分よりも大きい,つまり高い偏差と低い偏差である.

実際,エラーを最小限にするために,モデルを選択するときに,バイアスとバリアンスの比率をバランスする必要があります.

偏差と差異とモデルの複雑性の関係は,次の図でより明確に示されています.

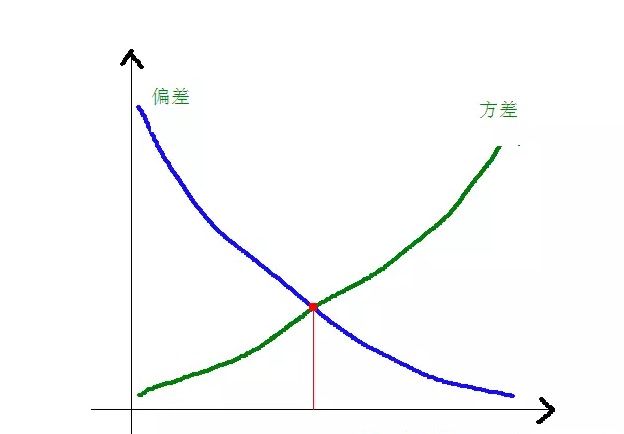
机器学习8大算法比较

モデルの複雑性が上昇するにつれて,偏差は徐々に小さくなり,偏差は徐々に大きくなります.

一般的なアルゴリズムのメリットとデメリット
- ###1. 朴素なベイエス
純粋なベイエスは生成モデル (生成モデルと判定モデルについて,主に結合分布を要求するかどうかについて) に属し,非常に単純で,あなたは単に数値の山を行います.

条件独立仮定 (より厳格な条件) を押した場合,単純なベイエス分類器の収束速度は,論理回帰のようなモデルを判別するよりも速いので,訓練データも少なく必要である.NB条件独立仮定が成立しない場合でも,NB分類器は実用では依然として優れた性能を示している.

その主な欠点は,特徴間の相互作用を学ぶことができないことであり,mRMRではRは特徴の冗長である.より古典的な例を引用すると,例えば,あなたがブラッド・ピットとトム・クルーズの映画が好きだが,彼らが一緒に演じる映画を嫌うことを学ぶことができない.

利点は:

朴素なベイエスモデルは,古典的な数学理論から生まれ,堅牢な数学的な基礎と安定した分類効率を有する. 小規模なデータに対して良好なパフォーマンスで,マルチクラスのタスクを単独で処理することができ,増量訓練に適しています. 欠落したデータに敏感ではない,アルゴリズムは比較的シンプルで,テキスト分類に使用されている. 欠点:

初期確率を計算する必要があります. 格付け決定の誤差率は; 輸入されたデータの表現形式に敏感である.
- ### 2.論理的回帰
判断型モデルには,規則化モデル (L0,L1,L2,etc) の方法がたくさんあり,そして,あなたの特徴が関連性があるか心配する必要はありません.

意思決定ツリーとSVMの比較では,かなり良い確率説明が得られ,新しいデータを使ってモデルを簡単に更新することもできます (オンライングラデントデッセンスのアルゴリズムを使います).

確率構造 (例えば,分類の限界値を単純に調整したり,不確実性を示したり,信頼区間を得るために) が必要である場合,または後でより多くのトレーニングデータをモデルに迅速に統合したい場合は,それを使用してください.

シグモイド関数:

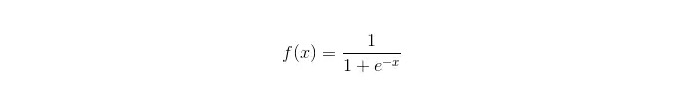
利点は: シンプルで幅広い産業用問題を実現する. 格納する際の計算量は非常に小さく,速度も速い,貯蔵資源も少ない. 簡単な観察サンプル確率スコア論理回帰の観点から,多重共線性は問題ではなく,L2正規化と組み合わせて解決できる. 欠点: 特性空間が大きいとき,論理回帰の性能は良くない. 適不適格で,一般的には正確性が低い. 複数の特徴や変数をうまく処理できない. 2つの分類問題しか処理できない (この基礎から派生したsoftmaxは多種分類に使用できる) と,線形に分ける必要がある. 線形でない特徴は変換が必要である.
- 線形回帰が3つあります
線形回帰は回帰のために用いられるが,論理回帰は分類のために用いられるが,その基本的な考えは,梯次下降法で最小二乗形式の誤差関数を最適化することである.当然,正規方程式で直接参数を解くこともできる.結果として:

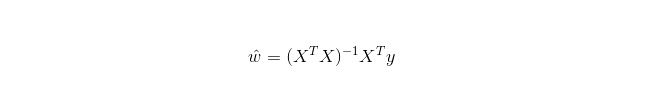
LWLR (局部加重線形回帰) では,参数の計算式は:

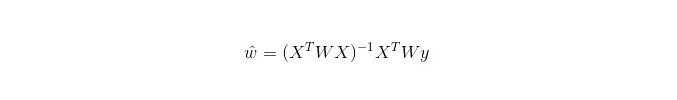
LWLRはLRとは異なり,LWLRは非パラメータモデルであり,回帰計算を行うたびに訓練サンプルを少なくとも1回横断しなければならない.

利点は:実現が簡単,計算が簡単.

欠点:非線形データに対応できない.
- ### 4.近隣のアルゴリズムはKNN
KNNは近隣アルゴリズムで,主なプロセスは以下の通りです.
```
   1. 计算训练样本和测试样本中每个样本点的距离(常见的距离度量有欧式距离，马氏距离等);

   2. 对上面所有的距离值进行排序;

   3. 选前k个最小距离的样本;

   4. 根据这k个样本的标签进行投票，得到最后的分类类别;
```
最適なK値を選ぶのはデータによって決まる. 一般的に,分類時により大きなK値がノイズの影響を軽減する.しかし,カテゴリー間の境界は曖昧になる.

よりよいK値は,例えば交差検証などの様々なインスピレーション技術によって得られる.さらに,ノイズと非関連性特征ベクトルの存在は,K近隣アルゴリズムの精度を低下させる.

近隣アルゴリズムは強い一貫性を持つ結果である. データが無限に近づくにつれて,アルゴリズムの誤差率はベイエスの誤差率の2倍を超えないことを保証する. いくつかの良いK値に対して,K近隣アルゴリズムの誤差率はベイエスの理論誤差率を超えないことを保証する.

KNNアルゴリズムの利点

理論は成熟し,考えはシンプルで,分類と回帰の両方をするために使用できます. 非線形分類に使用できます. 訓練時間の複雑性はO (n) である. データの仮定はなく,精度は高く,アウトリアには敏感ではありません. 欠点

コンピュータは大きい. サンプル不均衡問題 (例えば,あるカテゴリーのサンプルの数は多く,他のカテゴリーのサンプルの数は少ない) 記憶力が多く必要で,
- ### 5. 意思決定の樹
簡単に説明できます. 特徴間の相互作用をストレスのない方法で処理し,非パラメータ化されているため,異常値やデータの線形分解性について心配する必要はありません (例として,決定樹は,特定の特徴の次元xの端でカテゴリーAを簡単に処理し,中間でカテゴリーBを処理し,次にカテゴリーAが特徴の次元xの前端に現れる場合など).

オンライン学習をサポートしていないことへの欠点の一つは,新しいサンプルが来ると,意思決定ツリーが完全に再構築される必要があることです.

また,適正化が容易であるという欠点は,ランダムフォレストRF (Random Forest RF) やツリーブーストドリー (Tree Boosted Tree) のような統合方法への切り口でもある.

さらに,ランダムフォレストは多くの分類問題で勝者であり (通常はサポートベクトルよりも少し優れている),迅速で調節可能で,サポートベクトルのように多くのパラメータを調節する必要がないことを心配する必要がないため,以前から人気がありました.

意思決定ツリーの重要な点は,分岐する属性を選択することなので,情報増強の計算式に注意を払い,それを深く理解することです.

この情報パネルの計算式は以下の通りです.

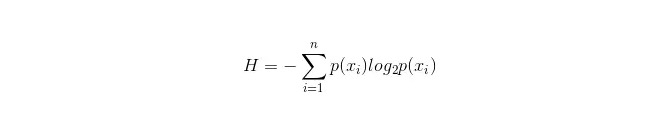
この n の代表は,n の分类カテゴリー (例えば,n=2) を有する.この 2 つのサンプルが総サンプルに現れる確率 p1 と p2 をそれぞれ計算し,未選択属性分岐前の情報を計算する.

現在,枝分けるために使用される属性xixiが選択され,このときの枝分けるルールは,xi=vxi=vの場合,サンプルを木の1つの枝に分割する.等しくない場合は別の枝に移動する.

明らかに,分岐中のサンプルには2つのカテゴリーが含まれている可能性が高い.分岐後の総情報分岐 H =p1 H1+p2 H2 を計算すると,このときの情報増幅 ΔH = H−H である.情報増幅の原則として,すべての属性をテストし,最大増幅をもたらす属性をこの分岐属性として選択する.

意思決定ツリーの利点

計算はシンプルで,理解しやすく,説明が容易です. 欠陥のある属性を扱うのに適したサンプルを比較する. 関連のない特性を処理できる. 比較的短い時間で,大規模なデータソースで実行可能な効果のある結果を得ることができる. 欠点

適正化が容易である (ランダムな森林は適正化を大幅に減らすことができます) データの関連性を見失い, 各カテゴリーからサンプル数が一致しないデータに対して,意思決定ツリー内の情報増強の結果は,より多くの数値を持つ特性に偏りがある (例えばRFのような情報増強を使用する限り,このデメリットがある).
- ### 5.1 適応する
アダボストは,前回のモデルの誤差率に基づいて構築された各モデルの加算モデルであり,誤差分別したサンプルに過剰な注意を払い,正しい分類されたサンプルに注意を減らして,繰り返し繰り返した後,比較的優れたモデルを得ることができる.

利点

アダボストは高度な精度を持つ分類器である. 様々な方法によってサブクラッサーを構築することができる. Adaboost アルゴリズムが提供しているのはフレームワークである. 単純な分類器を使用すると,計算結果が理解可能であり,弱い分類器の構成は極めてシンプルである. シンプルで,フィーチャーフィルタは必要ありません. オーバーフィッティングは容易ではありません. ランダムフォレストやGBDTなどの組み合わせアルゴリズムについては,この記事を参照してください:機械学習 - 組み合わせアルゴリズムの概要

デメリット: アウトリアに敏感
- ### 6.SVMはベクトルマシンをサポートします
高精度で,過剰なフィットメントを避けるための優れた理論的保証を提供し,データも原特征空間で線形に分けられない場合でも,適切な核関数を与えればうまく動作する.

動作する超高次元テキスト分類問題では特に人気がある.残念ながらメモリ消費が高く,説明が難しく,実行と調節も少し面倒だが,ランダムフォレスはこれらの欠点を回避して,比較的便利である.

利点巨大な特徴空間という高次元の問題を解決できます. 線形でない特徴の相互作用を処理できる. データをすべて頼りにする必要はありません. 広める能力が向上します.

欠点検知サンプルが多くある場合,効率はあまり高くない. 非線形問題には一般的な解がないため,適切な核関数を見つけるのは時には困難です. 欠落したデータに対して敏感です. 核の選択も巧妙である (libsvmには4つの核関数があります:線形核,多項核,RBF,シグモイド核):

まず,サンプル数が特徴数より小さい場合,非線形核を選択する必要はありません.

2つ目は,サンプル数が特徴数よりも大きい場合,非線形核を使用してサンプルをより高い次元にマッピングすることで,一般的により良い結果が得られる.

第3に,サンプル数と特徴数が等しい場合,非線形核を用いることができる.

最初のケースでは,データを最初にリデミネートし,非線形コアを使用することもできます.これはまた方法です.
- ### 7. 人工神経ネットワークの利点とデメリット
ニューラルネットワークの利点は: クラシック音楽は, 配列分散処理能力,分散ストレージ,学習能力が強い. 騒音神経に対する強硬さと容赦性があり,複雑な非線形関係に十分接近する. フォトグラフィーは,フォトグラフィーは,フォトグラフィーは

ニューラルネットワークの欠点: 神経ネットワークには,ネットワークトポログラフィの構造,重み値,値などの多くのパラメータが求められます. 観察できない学習プロセス,説明が難しい出力結果,結果の信頼性や可接受性に影響を与える. 学習時間が長すぎたり,目的を達成することさえできないかもしれません.
- ### 8 K-Means グループ
K-Meansの分類に関する記事を書きました. ブログリンク: 機械学習アルゴリズム-K-meansの分類.

利点簡単なアルゴリズムで,実行が簡単です. このアルゴリズムは,大データセットを処理する際には,その複雑性が約O (nkt) であるため,比較的スケーラブルで効率的です.nはすべてのオブジェクトの数,kはの数,tは繰り返しの数です.通常はk<<です. アルゴリズムは,平方差関数の最小値を出すkの分子を探す. が密集し,球状または結束状で,との区別がはっきりしているとき,群組効果はよりよい.

欠点数値型データに適したデータ型に対する要求が高く, 局所最小値に収束する可能性がありますが,大規模なデータでは収束が遅い K値は選択するのが難しい. 初期値に対する心値に敏感で,異なる初期値に対して異なるグループ化結果をもたらす可能性があります. の形状は,の形状と形状の違いが大きいの形状と形状の違いが大きいの形状と形状が異なるの形状が異なるの形状と形状が異なるの形状が異なるの形状と形状が異なるの形状が異なるの形状と形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形状が異なるの形が異なるの形が異なるの形が異なるの形が異なるの形が異なるの形が異なるの形が異なるの形が異なるの形が異なるノイズと隔離点データに敏感で,この種のデータの一部は平均値に大きな影響を与える.

アルゴリズムによる参照の選択

外国語の翻訳をした記事の一つは,簡単なアルゴリズム選択のコツを示しています.

論理回帰が最初に選択されるべき場合,その効果がうまくいかない場合,その結果を基調として参照し,その基礎を他のアルゴリズムと比較することができます.

決定樹 (random forest) を試して,モデルの性能を大幅に向上させることができるか見てみましょう. 最終モデルとして,それを使っていない場合でも,ノイズ変数を削除し,特徴を選択するために,random forest を使用できます.

特徴の数と観察サンプルが特に多くなった場合,リソースと時間が充実しているときに (この前提は重要) SVMを使用することは選択肢である.

通常の場合:GBDT>=SVM>=RF>=Adaboost>=Other...ああ,今,ディープラーニングは人気があり,多くの分野で使用されています. それは神経ネットワークに基づいています.

アルゴリズムは重要ですが,良いデータは良いアルゴリズムよりも優れています.優れた特徴をデザインすることは非常に有益です. あなたが超大型データセットを持っている場合,どのアルゴリズムを使おうとも,分類性能に大きな影響を与えない可能性があります. (このとき,速度と使いやすさに基づいて選択することができます).
参考文献

もっと見る

2019 - FMZ - 発明者定量化

機械学習の8大アルゴリズム比較

機械学習の8大アルゴリズム比較

一般的なアルゴリズムのメリットとデメリット

参考文献