ニューラルネットワークとデジタル通貨量的な取引シリーズ (1) - LSTMはビットコイン価格を予測

ニューラルネットワークとデジタル通貨量的な取引シリーズ (1) - LSTMはビットコイン価格を予測

1. 簡潔 な 紹介

ディープニューラルネットワークは,近年,ますます普及している.多くの分野で過去に解決できなかった問題を解決し,強力な能力を実証している.時間系列の予測において,一般的に使用されるニューラルネットワーク価格はRNNであり,現在のデータ入力だけでなく,歴史的なデータ入力も持っている.もちろん,RNN価格予測について話すとき,私たちはしばしばRNNの1つであるLSTMについて語ります.この論文は,PyTorchに基づいてビットコインの価格を予測するためのモデルを構築します.インターネット上には多くの関連情報がありますが,まだ十分に徹底していません.PyTorchを使用する人は比較的少ないです.まだ記事を書く必要があります.最終結果は,開通価格,閉通価格,最高取引価格,最低価格,Bitcoinの閉通価格を予測することです.私の個人的な知識は,PyTorchの知識と訂正を希望します. このチュートリアルは FMZ Quant Trading プラットフォームによって作成されています (www.fmz.com) QQグループに参加してください: 863946592 コミュニケーションのために.

2.データと参照

ビットコインの価格データは FMZ Quant トレーディングプラットフォームから入手:https://www.quantinfo.com/Tools/View/4.htmlわかった 関連した価格予測の例:https://yq.aliyun.com/articles/538484わかった RNNモデルについて詳細な説明:https://zhuanlan.zhihu.com/p/27485750わかった RNNの入力と出力を理解する:https://www.zhihu.com/question/41949741/answer/318771336わかった 公式のドキュメント:https://pytorch.org/docs他の情報は自分で検索できます. この記事を読むには パンダ/パイソン/データ処理などの知識が必要ですが,そうでない場合も構いません.

3. ピトーチ LSTM モデルのパラメータ

LSTMのパラメータ:

文書の密度の高いパラメータを見たとき 私の反応は "これは何だ?"でした

ゆっくり読みながら,ようやく理解した.

input_size: ベクトル x の特徴的なサイズを入力します. 閉じる価格が閉じる価格で予測されている場合, input_size=1; 閉じる価格が高開閉値で予測されている場合, input_size=4.hidden_size: 暗黙の層サイズnum_layers: RNNの層数batch_first: true の場合,最初の入力次元は batch_size で,これは非常に混乱し,下記で詳細に説明します.

データパラメータを入力します:

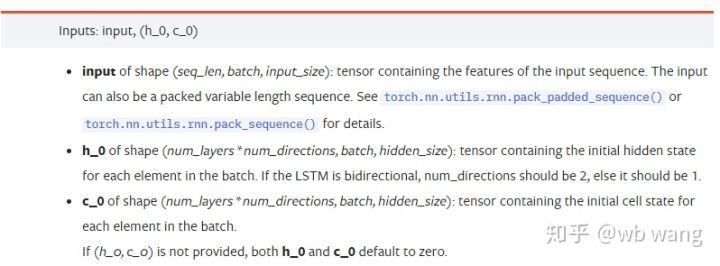
input: 特定の入力データは三次元テンソールで,特定の形は: (seq_len, batch, input_size). ここで, seq_len はシーケンスの長さ,すなわち,LSTM が歴史的データを考慮する必要がある時間を指します.これはLSTM の内部構造ではなく,データのフォーマットのみを指すことに注意してください.同じ LSTM モデルは異なる seqs_lens データを入力することができ,予測結果が得られます.バッチは,データの何つの異なるグループを表すバッチのサイズを指します.入力_サイズは前の入力_サイズです.h_0: 初期隠された状態,形状は (num_layers * num_directions, batch, hidden_size),双方向ネットワークの場合, num_directions=2.c_0: 細胞の初期状態,上記のような形状は指定できない.

出力パラメータ:

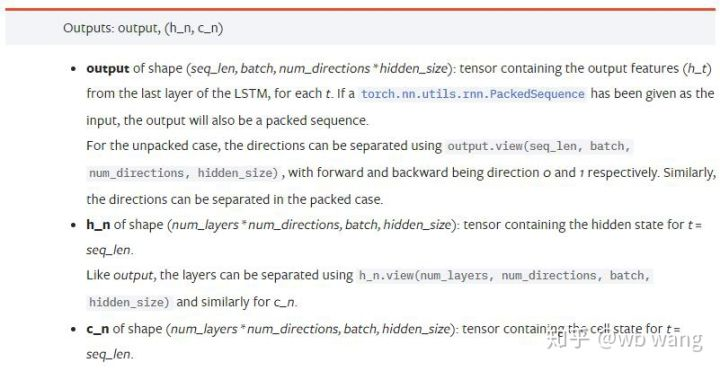
output:出力の形 (seq_len, batch, num_directions * hidden_size),それがモデルパラメータ batch_firstに関連していることに注意してください.h_n: t = seq_len のときの h 状態は,h_0 と同じ形である.c_n: t = seq_len のときの状態 c は,c_0 と同じ形状である.

4. LSTM 入力と出力の簡単な例

必要なパッケージを最初にインポートする

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

LSTM モデルを定義する

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

入力データを準備する

x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

xの形は (3,4,5) です.batch_first=Trueこのときの batch_size のサイズは 3 です. sqe_len は 4 です. input_size は 5 です. X [0] は最初のバッチを表します.

batch_first が定義されていない場合,デフォルト値は False で,この時点でデータ表示は完全に異なります.バッチサイズは 4,sqe_len は 3,input_size は 5.この時点で,x [0] は t=0 のときすべてのバッチのデータを表現します.この設定が直感的ではないと感じていますので,パラメータを追加しました.batch_first=True.

この2つの間のデータ変換も非常に便利です.x.permute (1,0,2)

入力と出力

LSTMの入力と出力の形は非常に混乱しており,次の図は理解するのに役立ちます.

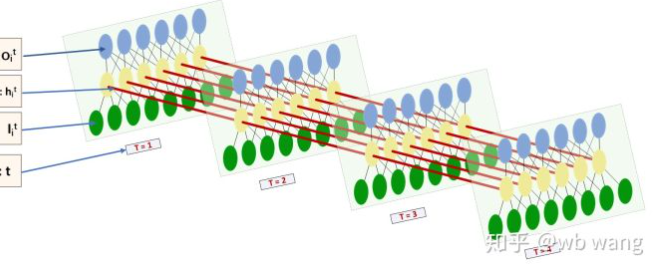
フォローしている:https://www.zhihu.com/question/41949741/answer/318771336.

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

前回のパラメータ解釈と一致する出力結果を観察します. hn.size() の第2値が 3 であることを注意してください.これは batch_size のサイズと一致します.つまり,中間状態は hn に保存されません.最後のステップのみが保存されます. LSTM ネットワークには 2 つのレイヤーがあるため,実際には hn の最後のレイヤの出力は出力の値です.出力の形は [3, 4, 10] で, t=0,1,2,3 のすべての時に結果を保存します.

hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. ビットコイン市場データを準備する

LSTMの入力と出力を理解することは非常に重要です.そうでなければ,インターネットからランダムにいくつかのコードを抽出することで間違いを犯すのは簡単です. LSTMの時間系列の強力な能力のために,モデルが間違っている場合でも,最終的には良い結果が得られます.

データ収集

Bitfinex Exchange の BTC_USD トレーディングペアの市場データは使用されます.

import requests
import json

resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

データ形式は以下のとおりです.

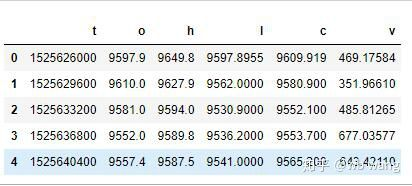
データの事前処理

df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.

データ標準化方法は非常に粗末で,いくつかの問題があるでしょう.ただ実証のために,返済率などのデータ標準化を使用できます.

訓練データを準備する

seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

train_x と train_y の最終形は:torch.Size ([800, 10, 5]),torch.Size ([800, 10, 1]).我々のモデルが 10 期間のデータに基づいて次の期間の終了価格を予測しているため,理論上は 800 のバッチがあり,予測された終了価格が 800 である限りである.しかし,各バッチの train_y には 10 のデータがある.実際には,各バッチ予測の中間結果は保留されている.最終損失を計算する際に,すべての 10 の予測結果を考慮し, train_y の実際の値と比較することができる.理論的には,最後の予測結果のみの Loss を計算することができます. LSTM モデルには実際に seq_lenful パラメータが含まれていないため,モデルは異なる長さに適用され,中間での予測結果は意味があり,私は Loss を組み合わせて計算することを好みます.

訓練データを準備するときに,ウィンドウの動きがジャンプし,すでに使用されているデータはもはや使用されないことに注意してください. もちろん,ウィンドウも一つずつ移動することができ,得られたトレーニングセットははるかに大きいです.しかし,隣接するバッチデータがあまりにも繰り返されていると感じたので,現在の方法を採用しました.

6. LSTM モデルを構築する

最終モデルは次のように作られ,2層のLSTMと1層のLinearを含む.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.

    def forward(self, x):
        x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.

7. モデル に 訓練 を 始める

最後に訓練を始めます コードは次のとおりです

criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
    out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # Reverse propagation losses
    optimizer.step() # Update parameters
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

訓練の結果は以下のとおりです.

8. モデル 評価

モデルの予測値:

p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

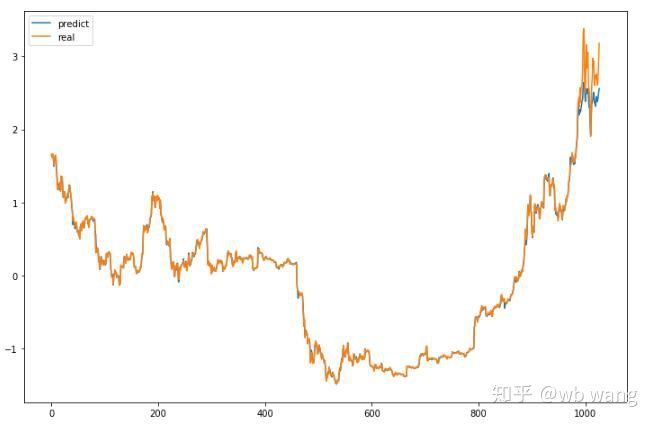
このグラフから,トレーニングデータ (800以前の) が非常に一貫していることがわかりますが,Bitcoinの価格は後期に上昇しています.モデルはこれらのデータを見ていないため,予測は不十分です.これはデータの標準化にも問題があることを示しています. 予測価格が正確ではないかもしれませんが,上昇と減少の予測の正確さはどれくらいですか? 予測データの断片を見てください.

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

その結果,上昇と減少を予測する精度率は81.4%に達し,私の期待を上回りました.何かおかしいのかわかりません.

もちろん,このモデルは実際のボットには適用されません. しかし,それは単純で理解しやすいです. それだけで始めます. 次に,デジタル通貨量化における神経ネットワークアプリケーションの入門コースが多くなります.