신경망 및 디지털 통화 양적 거래 시리즈 (1) - LSTM 비트코인 가격을 예측합니다

신경망 및 디지털 통화 양적 거래 시리즈 (1) - LSTM 비트코인 가격을 예측합니다

1. 간략 한 소개

딥 뉴런 네트워크는 최근 몇 년 동안 점점 더 인기를 끌고 있습니다. 많은 분야에서 과거에 해결할 수 없었던 문제를 해결하고 강력한 능력을 입증했습니다. 시간 시리즈 예측에서 일반적으로 사용되는 뉴런 네트워크 가격은 RNN입니다. 현재 데이터 입력뿐만 아니라 역사적 데이터 입력도 가지고 있기 때문입니다. 물론, RNN 가격 예측에 대해 이야기 할 때 우리는 종종 RNN 중 하나를 이야기합니다: LSTM. 이 논문은 PyTorch을 기반으로 비트코인 가격을 예측하는 모델을 구축합니다. 인터넷에 관련 정보가 많이 있지만 여전히 충분히 철저하지 않으며 PyTorch을 사용하는 사람들이 상대적으로 적습니다. 아직 기사를 작성해야합니다. 최종 결과는 오픈 가격, 폐쇄 가격, 최고 거래 가격, 가장 낮은 가격 및 비트코인의 다음 폐쇄 가격을 예측하는 것입니다. 제 개인적인 지식과 비판과 수정에 대한 뉴런 네트워크의 저 저감입니다. 이 튜토리얼은 FMZ 퀀트 트레이딩 플랫폼에 의해 제작되었습니다 (www.fmz.comQQ 그룹에 오신 것을 환영합니다: 863946592 통신.

2. 자료 및 참조

FMZ 퀀트 트레이딩 플랫폼에서 얻은 비트코인 가격 데이터:https://www.quantinfo.com/Tools/View/4.html- 그래요 가격 예측에 관련된 예시:https://yq.aliyun.com/articles/538484- 그래요 RNN 모델에 대한 자세한 소개:https://zhuanlan.zhihu.com/p/27485750- 그래요 RNN의 입력과 출력을 이해:https://www.zhihu.com/question/41949741/answer/318771336- 그래요 피토치에 대한 공식 문서:https://pytorch.org/docs다른 정보는 직접 검색하실 수 있습니다. 또한, 이 기사를 읽기 위해서는 판다/파이썬/데이터 처리와 같은 사전 지식이 필요하지만, 그렇지 않다면 상관없습니다.

3. 피토치 LSTM 모델의 매개 변수

LSTM의 매개 변수:

제가 이 문서에 있는 이 은 매개 변수를 처음 봤을 때 제 반응은 "이건 뭐야?

천천히 읽으면서 마침내 이해했어요.

input_size: 벡터 x의 특징 크기를 입력합니다. 닫기 가격이 닫기 가격에 의해 예측되는 경우, 입력_ 크기=1; 닫기 가격이 높은 개척과 낮은 폐쇄로 예측되는 경우, 입력_ 크기=4.hidden_size: 암시층 크기num_layers: RNN의 계층 수.batch_first: 만약 사실이라면 첫 번째 입력 차이는 batch_size 입니다. 또한 매우 혼란스럽고, 아래에서 자세히 설명될 것입니다.

데이터 매개 변수를 입력합니다:

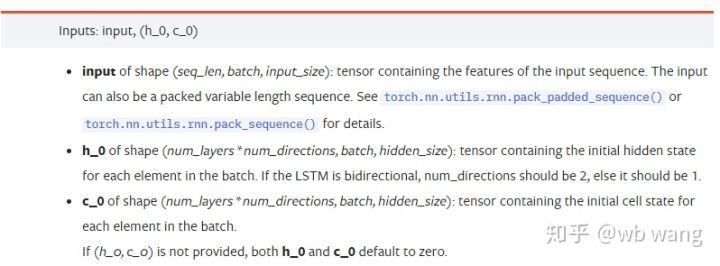
input: 특정 입력 데이터는 3차원 텐서이며, 특정 형태는: (seq_len, batch, input_size). 여기서, seq_len은 일련의 길이를 가리키며, 즉 LSTM가 역사적 데이터를 고려해야하는 시간이 얼마나 오래되는지 나타냅니다. 이것은 LSTM의 내부 구조가 아닌 데이터의 형식만을 가리키고 있음을 유의하십시오. 동일한 LSTM 모델은 예측 결과를 줄 수있는 다른 seqs_lens 데이터를 입력할 수 있습니다. batch는 일련의 크기를 가리키며, 얼마나 많은 다른 데이터 그룹을 나타냅니다. input_size는 이전 입력_size입니다.h_0: 초기 숨겨진 상태, 모양 (num_layers * num_directions, batch, hidden_size), 만약 쌍방향 네트워크라면, num_directions=2.c_0: 초기 세포 상태, 위와 같은 모양은 지정할 수 없습니다.

출력 파라미터:

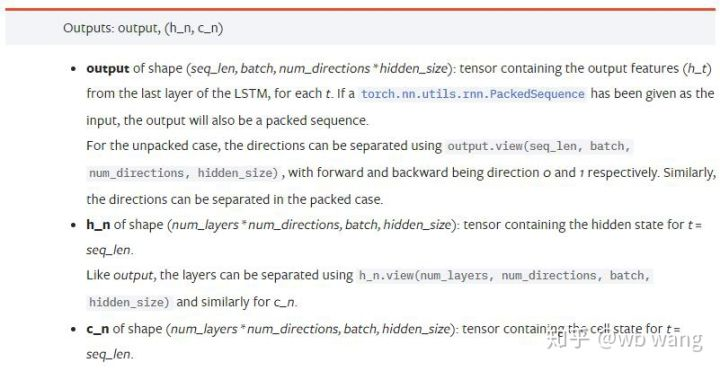
output: 출력의 형태 (seq_len, batch, num_directions * hidden_size), 그것은 모델 매개 변수 batch_first와 관련이 있음을 참고하십시오.h_n: t = seq_len의 순간 h 상태, h_0과 같은 모양c_n: t = seq_len의 순간에 c 상태, c_0과 같은 모양

4. LSTM 입력과 출력의 간단한 예

먼저 필요한 패키지를 가져오세요

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

LSTM 모델을 정의합니다

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

입력 데이터를 준비

x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

x의 모양은 (3,4,5) 입니다.batch_first=True이전에, 이 때 batch_size의 크기는 3, sqe_len는 4, input_size는 5. X [0]는 첫 번째 팩을 나타냅니다.

batch_first가 정의되지 않으면 기본 값은 False이므로 데이터 표현은 완전히 다릅니다. 팩 크기는 4, sqe_len는 3, input_size는 5. 이 때, x [0]는 t=0 때 모든 팩의 데이터를 나타냅니다. 이 설정이 직관적이지 않다고 생각합니다. 그래서 매개 변수를 추가했습니다.batch_first=True.

이 둘 사이의 데이터 변환도 매우 편리합니다.x.permute (1,0,2)

입력과 출력

LSTM의 입력과 출력의 형태는 매우 혼란스럽고 다음 그림은 이해하는데 도움이 될 수 있습니다.

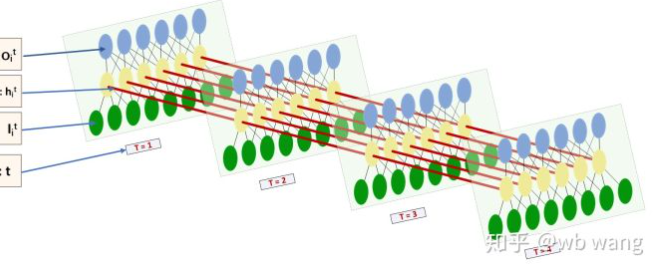
이쪽에서:https://www.zhihu.com/question/41949741/answer/318771336.

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

이전 매개 변수 해석과 일치하는 출력 결과를 관찰하십시오. hn.size() 의 두 번째 값이 3이며 batch_size의 크기와 일치한다는 것을 참고하십시오. 즉 중간 상태가 hn에 저장되지 않고 마지막 단계만 저장된다는 것을 의미합니다. 우리의 LSTM 네트워크는 두 계층을 가지고 있기 때문에, 사실 hn의 마지막 계층의 출력은 출력의 값입니다. 출력의 형태는 [3, 4, 10], t=0,1,2,3의 모든 시간에 결과를 저장합니다.

hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. 비트코인 시장 데이터를 준비

이전에도 많이 언급되었는데, 이것은 단지 시작일 뿐입니다. LSTM의 입력과 출력을 이해하는 것이 매우 중요합니다. 그렇지 않으면 인터넷에서 일부 코드를 무작위로 추출하여 실수를 쉽게 할 수 있습니다. 시간 계열에 대한 LSTM의 강력한 능력으로 인해 모델이 잘못되어도 결국 좋은 결과를 얻을 수 있습니다.

데이터 수집

Bitfinex 거래소에서 BTC_USD 거래 쌍의 시장 데이터를 사용합니다.

import requests
import json

resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

데이터 형식은 다음과 같습니다.

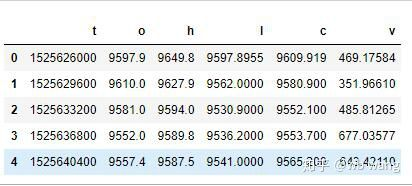
데이터 사전 처리

df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.

데이터 표준화 방법은 매우 거칠고, 몇 가지 문제가 있을 것입니다. 단지 시연을 위해, 당신은 반환률과 같은 데이터 표준화를 사용할 수 있습니다.

훈련 데이터를 준비

seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

train_x와 train_y의 최종 형태는: torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). 우리의 모델은 10개의 기간의 데이터에 기초하여 다음 기간의 종료 가격을 예측하기 때문에 이론적으로는 800개의 팩이 있습니다. 그러나 train_y는 각 팩에 10개의 데이터가 있습니다. 사실, 각 팩 예측의 중간 결과가 예약되어 있습니다. 최종 손실을 계산할 때, 모든 10개의 예측 결과를 고려하여 train_y의 실제 값과 비교할 수 있습니다. 이론적으로는 마지막 예측 결과의 손실만을 계산할 수 있습니다. LSTM 모델은 실제로 seq_lenful 매개 변수를 포함하지 않으므로 모델은 다른 길이에 적용될 수 있으며 중간에서의 예측 결과도 의미 있습니다. 그래서 나는 손실을 결합하고 계산하는 것을 선호합니다.

훈련 데이터를 준비 할 때 창의 움직임이 점프되고 이미 사용 된 데이터가 더 이상 사용되지 않는다는 점에 유의하십시오. 물론 창은 하나씩 움직일 수도 있으므로 얻은 훈련 세트가 훨씬 커집니다. 그러나 인접한 팩 데이터가 너무 반복되는 것을 느꼈기 때문에 현재 방법을 채택했습니다.

6. LSTM 모델을 구축

최종 모델은 다음과 같이 구성되어 있으며, 2층 LSTM와 선형 층을 포함합니다.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.

    def forward(self, x):
        x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.

7. 모델 을 훈련 시키기 시작 하라

마침내 훈련이 시작됩니다. 코드는 다음과 같습니다.

criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
    out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # Reverse propagation losses
    optimizer.step() # Update parameters
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

교육의 결과는 다음과 같습니다.

8. 모델 평가

모델의 예측 값:

p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

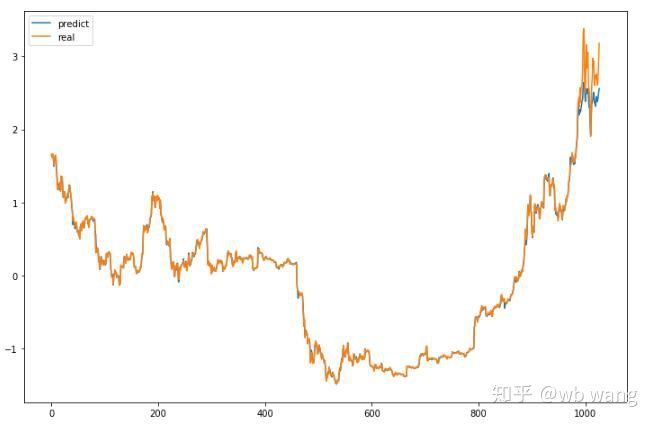
차트에서 볼 수 있듯이 훈련 데이터 (800 이전) 는 매우 일관성이 있지만, 비트코인의 가격은 후기 기간에 상승했습니다. 모델은 이러한 데이터를 보지 못했기 때문에 예측이 불충분합니다. 이것은 또한 데이터 표준화에 문제가 있음을 보여줍니다. 예측된 가격은 정확하지 않을 수도 있지만, 증가와 감소의 예측의 정확도는 무엇입니까? 예측 데이터의 세그먼트를 살펴보십시오.

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

그 결과 상승과 하락을 예측하는 정확도는 81.4%에 달했습니다. 여전히 기대를 초과했습니다. 뭔가 잘못되었는지 모르겠습니다.

물론, 이 모델은 실제 봇에 적용되지 않지만 간단하고 이해하기 쉽다. 그냥 그것과 시작. 다음, 디지털 통화 정량화에 신경 네트워크 응용의 더 많은 도입 과정이있을 것입니다.