Sumber dimuat naik... memuat...

Perbandingan 8 algoritma pembelajaran mesin

Penulis:Pencipta Kuantiti - Impian Kecil, Dicipta: 2016-12-05 10:42:02, Dikemas kini:

Perbandingan 8 algoritma pembelajaran mesin

Dalam artikel ini, kita akan membincangkan beberapa senario penyesuaian algoritma yang biasa digunakan dan kelebihan dan kekurangannya!

Terdapat begitu banyak algoritma pembelajaran mesin, dalam bidang pengelompokan, regresi, pengelompokan, rekomendasi, pengenalan imej, dan lain-lain, untuk mencari algoritma yang sesuai tidak begitu mudah, jadi dalam aplikasi sebenar, kita biasanya menggunakan pembelajaran inspirasi untuk bereksperimen.

Biasanya, kita akan mulakan dengan memilih algoritma yang disetujui oleh semua orang, seperti SVM, GBDT, Adaboost, dan sekarang pembelajaran mendalam sangat popular, dan rangkaian saraf juga merupakan pilihan yang baik.

Jika anda peduli dengan ketepatan, kaedah terbaik adalah dengan menguji setiap algoritma secara berasingan melalui pengesahan silang, membandingkannya, dan kemudian menyesuaikan parameter untuk memastikan setiap algoritma mencapai yang terbaik, dan akhirnya memilih yang terbaik.

Tetapi jika anda hanya mencari algoritma yang cukup baik untuk menyelesaikan masalah anda, atau ada beberapa petua yang boleh anda rujuk, berikut adalah analisis kelebihan dan kekurangan setiap algoritma, berdasarkan kelebihan dan kekurangan algoritma, lebih mudah untuk memilihnya.

Perbezaan & Perbezaan

Dalam statistik, model yang baik atau buruk adalah diukur berdasarkan kesesuaian dan perbezaan, jadi mari kita umumkan kesesuaian dan perbezaan terlebih dahulu:

Penyimpangan: menggambarkan jurang antara nilai ramalan (nilai anggaran) yang dijangkakan E dan nilai sebenar Y. Semakin besar penyimpangan, semakin jauh data sebenar.

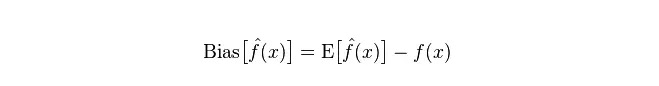
Perbezaan: menerangkan pelbagai perubahan dalam nilai ramalan P, tahap pemisahan, adalah perbezaan antara nilai ramalan, iaitu jarak dari nilai E yang diharapkan. Semakin besar perbezaannya, semakin tersebarnya data.

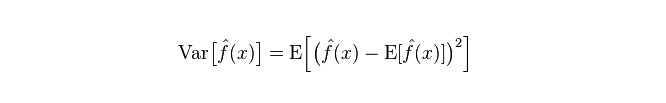
Kesalahan sebenar model adalah jumlah kedua-duanya, seperti yang ditunjukkan di bawah:

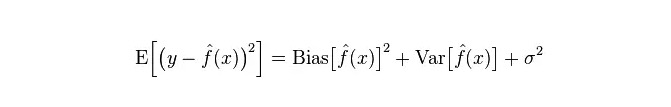
Jika satu set latihan kecil, pengelasan dengan kebelakangan tinggi/kebelakangan rendah (contohnya, Bayes NB yang sederhana) akan lebih baik daripada pengelasan dengan kebelakangan rendah/kebelakangan tinggi (contohnya, KNN) kerana yang kedua akan terlalu sesuai.

Walau bagaimanapun, apabila kumpulan latihan anda semakin besar, model akan menjadi lebih baik untuk meramalkan data asal, dan kesesuaian akan berkurangan, di mana pengelas kesesuaian rendah / tinggi akan menunjukkan kelebihan mereka secara beransur-ansur (kerana mereka mempunyai kesesuaian mendekat yang lebih rendah), di mana pengelas kesesuaian tinggi tidak lagi mencukupi untuk memberikan model yang tepat.

Sudah tentu, anda juga boleh menganggap ini sebagai perbezaan antara model penjanaan (NB) dan model penilaian (KNN).

Mengapa Bayes yang sederhana mempunyai kecacatan yang tinggi dan kecacatan yang rendah?

Di bawah ini adalah maklumat yang saya terima:

Pertama, anggap anda tahu hubungan antara set latihan dan set ujian. Secara ringkasnya, kita akan belajar model pada set latihan dan kemudian mengambil set ujian untuk digunakan, dan hasilnya akan diukur berdasarkan kadar ralat set ujian.

Tetapi selalunya, kita hanya boleh menganggap bahawa kumpulan ujian dan kumpulan latihan sesuai dengan pembahagian data yang sama, tetapi tidak mendapat data ujian yang sebenarnya.

Oleh kerana sampel yang dilatih adalah sedikit (sekurang-kurangnya tidak mencukupi), maka model yang diperoleh melalui set latihan tidak selalu benar-benar betul. Walaupun 100% kebenarannya pada set latihan tidak menunjukkan bahawa ia menggambarkan sebaran data yang benar, perlu diketahui bahawa tujuan kami adalah untuk menggambarkan sebaran data yang benar, bukan hanya menggambarkan titik data terhad dalam set latihan.

Selain itu, dalam praktiknya, sampel latihan sering mempunyai kesalahan kebisingan tertentu, jadi jika terlalu berusaha untuk mencapai kesempurnaan pada set latihan, model yang rumit akan menyebabkan model memperlakukan semua kesilapan dalam set latihan sebagai ciri pembahagian data yang benar, dan dengan itu mendapat anggaran pembahagian data yang salah.

Dengan cara ini, set ujian yang sebenarnya akan menjadi salah (yang dipanggil fit) ; tetapi juga tidak boleh menggunakan model yang terlalu mudah, jika tidak, model tidak akan mencukupi untuk melukiskan pembahagian data ketika pembahagian data agak rumit (yang menunjukkan kadar ralat yang tinggi walaupun pada set latihan, yang lebih kurang fit).

Model yang terlalu sesuai menunjukkan model yang digunakan lebih rumit daripada pembahagian data yang sebenarnya, sementara model yang kurang sesuai menunjukkan model yang digunakan lebih mudah daripada pembahagian data yang sebenarnya.

Dalam kerangka pembelajaran statistik, terdapat pandangan bahawa apabila orang melukis kerumitan model, Error = Bias + Variance. Di sini, Error mungkin dapat difahami sebagai kadar ralat ramalan model, yang terdiri daripada dua bahagian, satu bahagian adalah bias yang tidak tepat yang disebabkan oleh model yang terlalu mudah, dan satu lagi adalah ruang perubahan dan ketidakpastian yang lebih besar yang disebabkan oleh model yang terlalu kompleks.

Oleh itu, ia adalah mudah untuk menganalisis Bayesian sederhana. Ia adalah model yang sangat disederhanakan, yang secara sederhana menganggap data tidak berkaitan. Oleh itu, untuk model sederhana seperti itu, kebanyakan kes akan mempunyai bahagian Bias yang lebih besar daripada bahagian Variance, iaitu perpindahan tinggi dan perpindahan rendah.

Dalam praktiknya, untuk meminimumkan kesilapan, kita perlu menyeimbangkan perkadaran Bias dan Variance semasa memilih model, iaitu menyeimbangkan over-fitting dan under-fitting.

Hubungan antara kesesuaian dan perbezaan dengan kerumitan model lebih jelas dengan menggunakan gambar berikut:

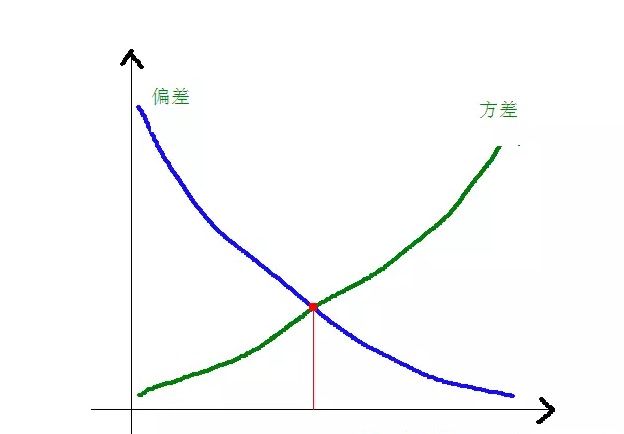
Apabila kompleksiti model meningkat, kesesuaian akan menjadi lebih kecil dan kesesuaian akan menjadi lebih besar.

Kelemahan algoritma biasa
- 1.朴素贝叶斯
  
  Bayes yang sederhana adalah model generatif (tentang model generatif dan model penentuan, terutama mengenai sama ada ia memerlukan pengedaran gabungan), sangat mudah, anda hanya melakukan banyak pengiraan.
  
  Jika anda meletakkan hipotesis kemerdekaan bersyarat (yang merupakan syarat yang lebih ketat), kelajuan penggundulan pempelajar Bayesian yang sederhana akan lebih cepat daripada model yang ditentukan, seperti regresi logik, jadi anda hanya memerlukan data latihan yang lebih sedikit. Walaupun hipotesis kemerdekaan bersyarat NB tidak berlaku, pempelajar NB masih berfungsi dengan baik dalam amalan.
  
  Kelemahan utamanya ialah ia tidak dapat mempelajari interaksi antara ciri-ciri, dengan menggunakan RMR dalam R, iaitu ciri-ciri yang tidak diperlukan. Sebagai contoh, walaupun anda menyukai filem Brad Pitt dan Tom Cruise, ia tidak dapat mempelajari filem yang anda tidak suka bersama mereka.
  
  Kelebihan:
  
  Model Bayesian sederhana berasal dari teori matematik klasik, mempunyai asas matematik yang kukuh, dan kecekapan klasifikasi yang stabil. Berprestasi baik untuk data kecil, dapat menangani tugas pelbagai kelas secara individu, sesuai untuk latihan kuantitatif; Algoritma yang lebih mudah dan mudah digunakan untuk mengelaskan teks. Kelemahan:
  
  Perkiraan kebarangkalian sebelum ini perlu dihitung; Peringkat kesilapan dalam membuat keputusan klasifikasi; Ia sangat sensitif terhadap bentuk ungkapan data yang dimasukkan.
- 2.逻辑回归
  
  Terdapat banyak kaedah untuk model normalization (L0, L1, L2, dan lain-lain), dan anda tidak perlu bimbang sama ada ciri anda berkaitan seperti dengan Bayesian sederhana.
  
  Anda juga akan mendapat penjelasan kebarangkalian yang baik berbanding dengan pokok keputusan dan mesin SVM, dan anda juga boleh dengan mudah menggunakan data baru untuk mengemas kini model (menggunakan algoritma penurunan gradien dalam talian, penurunan gradien dalam talian).
  
  Jika anda memerlukan struktur kebarangkalian (contohnya, untuk menyesuaikan ambang klasifikasi, menunjukkan ketidakpastian, atau untuk mendapatkan selang kepercayaan), atau anda ingin mengintegrasikan data latihan yang lebih banyak ke dalam model dengan cepat pada masa akan datang, maka gunakan ia.
  
  Fungsi Sigmoid:
  
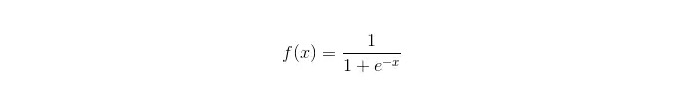
  Kelebihan: Mempunyai aplikasi yang mudah dan meluas untuk masalah industri; Pengiraan yang sangat kecil apabila dikategorikan, kelajuan yang cepat, sumber simpanan yang rendah; Skor kebarangkalian sampel pemerhatian yang mudah; Untuk regresi logik, kepelbagaian simetris tidak menjadi masalah, ia boleh disatukan dengan L2 normalisasi untuk menyelesaikan masalah ini; Kelemahan: Apabila ruang ciri besar, prestasi regresi logik tidak baik; Mudah tidak sesuai, secara amnya kurang tepat Tidak dapat menangani banyak ciri atau pembolehubah pelbagai jenis dengan baik; Hanya boleh menangani masalah dua klasifikasi (yang dihasilkan dari ini softmax boleh digunakan untuk pelbagai klasifikasi) dan mestilah terbahagi secara linear; Untuk ciri-ciri bukan linear, pemindahan diperlukan;
- 3.线性回归
  
  Regresi linear digunakan untuk regresi, tidak seperti regresi logistik yang digunakan untuk klasifikasi, yang idea asasnya adalah untuk mengoptimumkan fungsi ralat dalam bentuk penggandaan dua minimum dengan cara penurunan gradien, dan tentu saja juga dapat mencari penyelesaian parameter secara langsung dengan persamaan normal, yang menghasilkan:
  
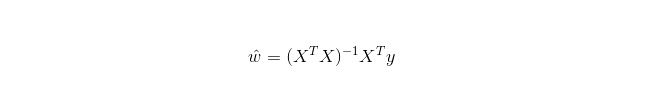
  Dalam LWLR (Local weighted linear regression), ungkapan pengiraan parameter ialah:
  
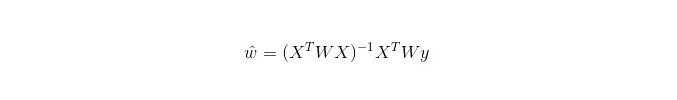
  Oleh itu, LWLR berbeza dengan LR, LWLR adalah model bukan parameter, kerana setiap kali pengiraan regresi perlu melalui sampel latihan sekurang-kurangnya sekali.
  
  Kelebihan: Mudah dilaksanakan, mudah dikira;
  
  Kelemahan: Tidak dapat menyesuaikan data bukan linear.
- 4.最近邻算法——KNN
  
  KNN adalah algoritma kejiranan terdekat, yang proses utamanya ialah:
  1. Mengira jarak setiap titik sampel dalam sampel latihan dan sampel ujian (pengukuran jarak biasa mempunyai jarak Eropah, jarak Mars, dan lain-lain);
  2. Mengurutkan semua nilai jarak di atas;
  3. Sampel k jarak minimum sebelum dipilih;
  4. Ujian ini dilakukan dengan mengundi tag k sampel untuk mendapatkan kategori peringkat akhir;
  Cara memilih nilai K yang optimum bergantung kepada data. Secara amnya, nilai K yang lebih besar dapat mengurangkan kesan kebisingan semasa pengelasan. Tetapi ia akan mengaburkan sempadan antara kategori.
  
  Nilai K yang lebih baik boleh diperoleh melalui pelbagai teknik penerangan, seperti pengesahan silang. Selain itu, kehadiran bunyi bising dan vektor ciri yang tidak berkaitan akan mengurangkan ketepatan algoritma K berdekatan.
  
  Algoritma berdekatan mempunyai hasil konsistensi yang lebih kuat. Dengan data yang cenderung ke had, algoritma menjamin bahawa kadar ralat tidak akan melebihi dua kali ganda kadar ralat algoritma Bayesian. Untuk beberapa nilai K yang baik, algoritma berdekatan menjamin bahawa kadar ralat tidak akan melebihi kadar ralat teoretis Bayesian.
  
  Kelebihan algoritma KNN
  
  Teori yang matang, pemikiran yang mudah, boleh digunakan untuk membuat klasifikasi dan regresi; boleh digunakan untuk pengelasan bukan linear; Kompleksiti masa latihan adalah O ((n); Tidak ada hipotesis terhadap data, ketepatan tinggi, tidak sensitif terhadap outlier; Kelemahan
  
  Perancangan besar; Masalah ketidakseimbangan sampel (iaitu, beberapa kategori mempunyai banyak sampel dan yang lain mempunyai sedikit); Menggunakan banyak memori.
- 5.决策树
  
  Mudah dijelaskan. Ia boleh mengendalikan hubungan interaksi antara ciri tanpa tekanan dan bukan parameter, jadi anda tidak perlu bimbang tentang nilai yang luar biasa atau data yang boleh dibahagikan secara linear (contohnya, pokok keputusan dapat dengan mudah mengendalikan kategori A di hujung dimensi x ciri, kategori B di tengah, dan kemudian kategori A muncul lagi di hujung depan dimensi x ciri).
  
  Salah satu kelemahan adalah bahawa ia tidak menyokong pembelajaran dalam talian, jadi pokok keputusan perlu dibina semula sepenuhnya setelah sampel baru tiba.
  
  Kelemahan lain adalah kesesuaian yang mudah berlaku, tetapi ini juga merupakan titik penempatan untuk pendekatan integrasi seperti hutan rawak RF (atau meningkatkan pokok yang didorong).
  
  Selain itu, hutan rawak sering menjadi pemenang dalam banyak masalah klasifikasi (biasanya sedikit lebih baik daripada mesin pembantu vektor), ia melatih dengan cepat dan boleh disesuaikan, dan anda tidak perlu risau untuk menyesuaikan banyak parameter seperti mesin pembantu vektor, jadi ia telah menjadi popular pada masa lalu.
  
  Satu perkara yang penting dalam pokok keputusan adalah memilih sifat untuk bercabang, jadi perhatikan formula pengiraan peningkatan maklumat dan fahamnya dengan mendalam.
  
  Permulaan pengiraan untuk information bar ialah sebagai berikut:
  
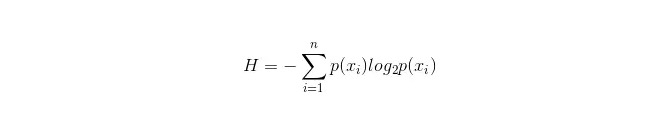
  Di mana n mewakili n kategori pembahagian (misalnya, andaikan masalah kategori 2, maka n = 2); perhitung kemungkinan kedua-dua sampel ini muncul dalam sampel keseluruhan masing-masing p1 dan p2, sehingga anda boleh mengira tanda maklumat sebelum cabang sifat yang tidak dipilih.
  
  Sekarang pilih sifat xixi untuk melakukan percabangan, di mana peraturan percabangan adalah: jika xi = vxi = v, percabangan sampel ke satu cawangan pokok; jika tidak sama, ke cawangan lain.
  
  Jelas sekali, sampel dalam cawangan kemungkinan besar terdiri daripada 2 kategori, iaitu H1 dan H2 untuk cawangan masing-masing, dan H1 = p1 H1 + p2 H2 untuk keseluruhan maklumat selepas cawangan, maka peningkatan maklumat ΔH = H - H. Dengan prinsip peningkatan maklumat, semua sifat diuji dan pilih sifat yang memberikan peningkatan terbesar sebagai sifat cawangan ini.
  
  Keuntungan Pokok Keputusan
  
  Perhitungan mudah, mudah difahami, mudah diterangkan; Perbandingan sampel yang sesuai untuk diuruskan dengan sifat yang hilang; Mampu menangani ciri-ciri yang tidak relevan; Hasil yang boleh dilaksanakan dan berkesan dapat dibuat pada sumber data besar dalam masa yang agak singkat. Kelemahan
  
  mudah berlaku overfitting (hutang rawak boleh mengurangkan overfitting dengan ketara); Perbezaan antara data dan data yang lain tidak dipertimbangkan. Untuk data yang mempunyai jumlah sampel yang tidak serasi dalam pelbagai kategori, hasil peningkatan maklumat di dalam pokok keputusan cenderung kepada ciri-ciri yang mempunyai nilai yang lebih banyak (yang mempunyai kelemahan ini selagi peningkatan maklumat digunakan, seperti RF).
- 5.1 Pengubahsuaian
  
  Adaboost adalah model penjumlahan, di mana setiap model dibina berdasarkan kadar ralat model sebelumnya, memberi perhatian yang berlebihan kepada sampel yang melakukan pembahagian ralat, dan memberi perhatian yang kurang kepada sampel yang diklasifikasikan dengan betul, untuk mendapatkan model yang agak baik selepas pengulangan berturut-turut.
  
  Kelebihan
  
  Adaboost adalah pengatur yang sangat tepat. Sub-pengurut boleh dibina dengan pelbagai kaedah, dan kerangka kerja yang disediakan oleh algoritma Adaboost. Hasil yang dikira dapat difahami apabila menggunakan pengelasan sederhana, dan pembinaan pengelasan lemah sangat mudah. Mudah, tidak perlu penyaringan ciri. Tidak mudah berlaku overfitting. Mengenai algoritma gabungan seperti Random Forest dan GBDT, lihat artikel ini: Machine Learning - Ringkasan Algoritma Gabungan
  
  Kelemahan: Lebih sensitif terhadap outlier
- 6.SVM支持向量机
  
  Kecekapan yang tinggi memberikan jaminan teori yang baik untuk mengelakkan pemasangan berlebihan, dan ia berfungsi dengan baik jika data tidak dapat dipisahkan secara linear dalam ruang ciri asal.
  
  Ia sangat popular dalam masalah klasifikasi teks yang sangat berdimensi tinggi. Malangnya, memori yang banyak digunakan dan sukar dijelaskan, operasi dan penyesuaian juga agak menyusahkan, tetapi hutan rawak hanya mengelakkan kelemahan ini, lebih praktikal.
  
  Kelebihan Ia boleh menyelesaikan masalah berdimensi tinggi, iaitu ruang ciri yang besar. Mampu menangani interaksi ciri-ciri bukan linear; Tidak perlu bergantung kepada keseluruhan data. Mempunyai peluang yang lebih baik untuk meningkatkan keupayaan generalisasi;
  
  Kelemahan Apabila banyak sampel diperhatikan, ia tidak begitu berkesan. Tidak ada penyelesaian universal untuk masalah bukan linear, dan kadang-kadang sukar untuk mencari fungsi teras yang sesuai; Mengenai data yang hilang; Pilihan untuk nukleus juga bijak (libsvm mempunyai empat fungsi nukleus: nukleus linear, nukleus multipolar, RBF dan nukleus sigmoid):
  
  Pertama, jika jumlah sampel kurang daripada bilangan ciri, maka tidak perlu memilih nukleus bukan linear, tetapi hanya menggunakan nukleus linear.
  
  Kedua, jika jumlah sampel lebih besar daripada bilangan ciri, maka nukleus bukan linear boleh digunakan untuk memetakan sampel ke dimensi yang lebih tinggi, yang biasanya memberikan hasil yang lebih baik.
  
  Ketiga, jika bilangan sampel dan bilangan ciri sama, maka keadaan ini boleh digunakan dengan nukleus bukan linear, prinsip yang sama seperti yang kedua.
  
  Untuk kes pertama, data boleh dimensionasi terlebih dahulu dan kemudian menggunakan teras bukan linear, yang juga merupakan satu kaedah.
- 7. Kelemahan dan kelemahan rangkaian saraf buatan
  
  Di samping itu, ia juga boleh digunakan untuk memaparkan maklumat mengenai sistem saraf. Peringkat yang tinggi; Kemahiran pemprosesan bersepadu, penyimpanan dan pembelajaran terdistribusi yang kuat. Kebolehan yang lebih kuat terhadap saraf bising dan toleransi kesalahan yang cukup untuk mendekati hubungan bukan linear yang kompleks; Ia mempunyai fungsi untuk mengingati kenangan.
  
  Kemudaratan rangkaian saraf buatan: Rangkaian saraf memerlukan banyak parameter, seperti struktur topologi rangkaian, nilai berat dan nilai awal ambang; Proses pembelajaran yang tidak dapat diobservasi, hasil output yang sukar dijelaskan, yang boleh mempengaruhi kredibiliti dan kebolehpercayaan hasil; Dalam kes ini, anda mungkin tidak dapat mencapai matlamat yang anda inginkan.
- 8 K-Means kumpulan
  
  Sebelum ini, saya telah menulis artikel mengenai K-Means Clustering, yang mempunyai pautan blog: Machine Learning Algorithm - K-Means Clustering.
  
  Kelebihan Algoritma mudah dan mudah dilaksanakan; Untuk memproses set data yang besar, algoritma ini agak berskala dan cekap kerana kompleksitinya adalah kira-kira O ((nkt), di mana n adalah jumlah semua objek, k adalah bilangan kerucut, dan t adalah jumlah pengulangan. Biasanya k<
  
  Kelemahan Keperluan untuk jenis data yang lebih tinggi dan sesuai untuk data berangka; Mungkin berkumpul kepada nilai minimum tempatan, lebih lambat untuk data besar Nilai K agak sukar untuk dipilih; Sensitiviti terhadap nilai awal, yang boleh menyebabkan hasil pengelompokan yang berbeza; Tidak sesuai untuk mencari kerucut yang tidak berbentuk konkrit, atau kerucut yang sangat berbeza saiznya. Data yang sensitif terhadap kerentanan dan titik terpencil boleh memberi kesan yang besar kepada purata.
  
  Algoritma memilih rujukan
  
  Dalam satu artikel yang telah diterjemahkan beberapa artikel dari luar negara sebelum ini, satu artikel memberikan satu teknik pilihan algoritma yang mudah:
  
  Yang pertama yang harus dipilih adalah regresi logik, dan jika hasilnya tidak baik, maka hasilnya boleh digunakan sebagai rujukan untuk membandingkan dengan algoritma lain.
  
  Kemudian cubalah pokok keputusan (Random Forest) untuk melihat apakah ia dapat meningkatkan prestasi model anda dengan ketara. Walaupun anda tidak menjadikannya sebagai model akhir, anda boleh menggunakan Random Forest untuk membuang pembolehubah bunyi, membuat pilihan ciri;
  
  Jika terdapat banyak ciri dan sampel yang diperhatikan, maka penggunaan SVM adalah pilihan apabila sumber dan masa mencukupi (premis ini penting).
  
  Biasanya: GBDT>=SVM>=RF>=Adaboost>=Other... oh, sekarang pembelajaran mendalam sangat popular, banyak bidang digunakan, ia berdasarkan rangkaian saraf, saya sendiri sedang belajar, hanya pengetahuan teori tidak begitu tebal, pemahaman tidak cukup mendalam, maka saya tidak akan memperkenalkannya di sini.
  
  Algoritma adalah penting, tetapi data yang baik lebih baik daripada algoritma yang baik, dan reka bentuk ciri yang baik sangat berguna. Jika anda mempunyai set data yang sangat besar, ia mungkin tidak memberi kesan yang besar kepada prestasi pengklasifikasian, tidak kira algoritma yang anda gunakan (di mana anda boleh membuat pilihan berdasarkan kelajuan dan kemudahan penggunaan).
Rujukan