Rangkaian Perdagangan Kuantitatif Rangkaian Rangkaian Rangkaian Neural dan Mata Wang Digital (1) - LSTM Meramalkan Harga Bitcoin

Rangkaian Perdagangan Kuantitatif Rangkaian Rangkaian Rangkaian Neural dan Mata Wang Digital (1) - LSTM Meramalkan Harga Bitcoin

1. Pengenalan ringkas

Rangkaian saraf dalam telah menjadi semakin popular dalam beberapa tahun kebelakangan ini. Ia telah menyelesaikan masalah yang tidak dapat diselesaikan pada masa lalu dalam banyak bidang dan telah menunjukkan keupayaannya yang kuat. Dalam ramalan siri masa, harga rangkaian saraf yang biasa digunakan adalah RNN, kerana ia tidak hanya mempunyai input data semasa, tetapi juga input data sejarah. Sudah tentu, apabila kita bercakap tentang ramalan harga RNN, kita sering bercakap tentang salah satu RNN: LSTM. Makalah ini akan membina model untuk meramalkan harga Bitcoin berdasarkan PyTorch. Walaupun terdapat banyak maklumat yang relevan di Internet, ia masih tidak cukup menyeluruh, dan masih ada agak sedikit orang yang menggunakan PyTorch. Adalah perlu untuk menulis artikel akhir. Hasilnya adalah menggunakan harga pembukaan, harga penutupan, harga perdagangan tertinggi, harga terendah, dan jumlah penutupan Bitcoin seterusnya. Saya berharap pengetahuan peribadi dan pengesahan dan pengesahan rangkaian saraf anda terhad. Tutorial ini dihasilkan oleh platform FMZ Quant Trading (www.fmz.comSelamat datang untuk menyertai kumpulan QQ: 863946592 untuk komunikasi.

2. Data dan rujukan

Data harga Bitcoin berasal dari platform FMZ Quant Trading:https://www.quantinfo.com/Tools/View/4.html- Tidak. Contoh ramalan harga yang berkaitan:https://yq.aliyun.com/articles/538484. Pengenalan terperinci kepada model RNN:https://zhuanlan.zhihu.com/p/27485750. Memahami input dan output RNN:https://www.zhihu.com/question/41949741/answer/318771336. Mengenai pytorch: dokumentasi rasmi:https://pytorch.org/docsUntuk maklumat lain, anda boleh mencari sendiri. Di samping itu, anda memerlukan beberapa pengetahuan sebelumnya untuk membaca artikel ini, seperti panda / python / pemprosesan data, tetapi tidak masalah jika anda tidak.

3. Parameter model LSTM pytorch

Parameter LSTM:

Kali pertama saya melihat parameter padat ini pada dokumen, tindak balas saya adalah: apa ini?

Semasa saya membaca perlahan-lahan, akhirnya saya faham.

input_size: Masukkan saiz ciri vektor x. Jika harga penutupan diramalkan oleh harga penutupan, maka input_size=1; Jika harga penutupan diramalkan oleh pembukaan tinggi dan penutupan rendah, maka input_size=4.hidden_size: Saiz lapisan tersiratnum_layers: Bilangan lapisan RNN.batch_first: Jika benar, dimensi input pertama adalah batch_size, yang juga sangat mengelirukan, dan ia akan diterangkan secara terperinci di bawah.

Masukkan parameter data:

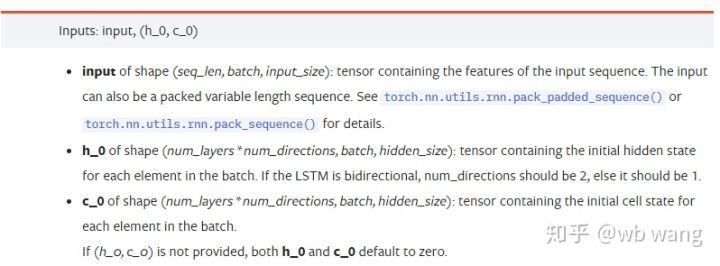
input: Data input tertentu adalah tensor tiga dimensi, dan bentuk tertentu adalah: (seq_len, batch, input_size). Di mana, seq_len merujuk kepada panjang urutan, iaitu berapa lama LSTM perlu mempertimbangkan data sejarah. Perhatikan bahawa ini merujuk kepada format data sahaja, bukan struktur dalaman LSTM. Model LSTM yang sama boleh memasukkan data seqs_lens yang berbeza, yang boleh memberikan hasil ramalan; batch merujuk kepada saiz kumpulan, mewakili berapa banyak kumpulan data yang berbeza; input_size adalah input_size sebelumnya.h_0: Keadaan tersembunyi awal, bentuk sebagai (num_layers * num_directions, batch, hidden_size), jika ia adalah rangkaian dua hala, num_directions=2.c_0: Keadaan sel awal, bentuk seperti di atas, boleh tidak ditentukan.

Parameter output:

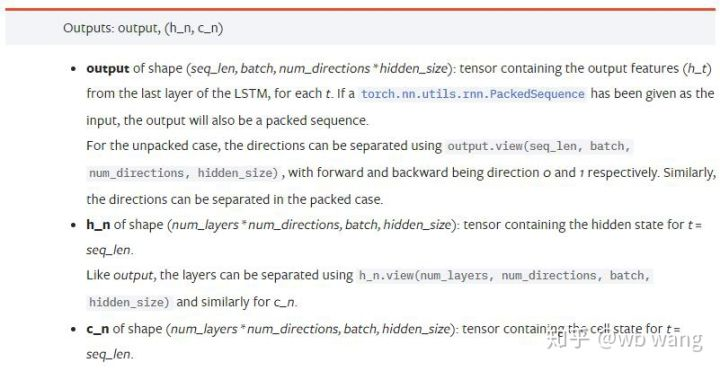
output: Bentuk output (seq_len, batch, num_directions * hidden_size), ambil perhatian bahawa ia berkaitan dengan model parameter batch_first.h_n: Keadaan h pada masa t = seq_len, bentuk yang sama dengan h_0.c_n: keadaan c pada masa t = seq_len, bentuk yang sama dengan c_0.

4. Contoh mudah input dan output LSTM

Memimport pakej yang diperlukan terlebih dahulu

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

Menentukan model LSTM

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

Sediakan data input

x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

Bentuk x ialah (3,4,5), kerana kita telah menentukanbatch_first=Truesebelum ini, saiz batch_size pada masa ini adalah 3, sqe_len adalah 4, input_size adalah 5. X [0] mewakili kumpulan pertama.

Jika batch_first tidak ditakrifkan, nilai lalai adalah False, maka perwakilan data sama sekali berbeza pada masa ini. saiz batch adalah 4, sqe_len adalah 3, input_size adalah 5. Pada masa ini, x [0] mewakili data semua batch apabila t = 0, dan sebagainya. Saya merasakan bahawa tetapan ini tidak intuitif, jadi saya menambah parameterbatch_first=True.

Penukaran data antara kedua-dua juga sangat mudah:x.permute (1,0,2)

Input dan output

Bentuk input dan output LSTM sangat mengelirukan, dan angka berikut dapat membantu kita memahami:

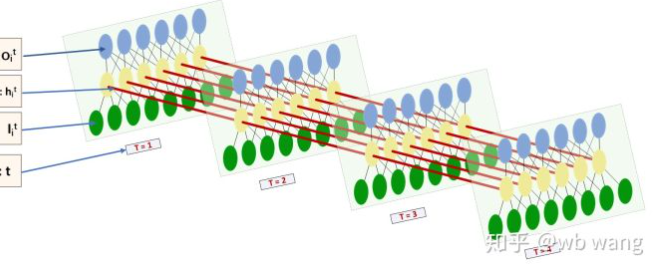
Dari:https://www.zhihu.com/question/41949741/answer/318771336.

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

Perhatikan hasil output, yang konsisten dengan tafsiran parameter sebelumnya. Perhatikan bahawa nilai kedua hn.size() adalah 3, yang konsisten dengan saiz batch_size, yang bermaksud bahawa keadaan pertengahan tidak disimpan di hn, hanya langkah terakhir disimpan. Oleh kerana rangkaian LSTM kami mempunyai dua lapisan, sebenarnya output lapisan terakhir hn adalah nilai output. Bentuk output adalah [3, 4, 10], yang menyimpan hasil pada semua masa t = 0,1,2,3, jadi:

hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. Sediakan data pasaran Bitcoin

Begitu banyak telah dikatakan sebelum ini, yang hanya permulaan. Adalah sangat penting untuk memahami input dan output LSTM. Jika tidak, mudah membuat kesilapan dengan mengekstrak beberapa kod secara rawak dari Internet. Kerana keupayaan LSTM yang kuat dalam siri masa, walaupun modelnya salah, hasil yang baik boleh diperoleh pada akhirnya.

Pemerolehan data

Data pasaran pasangan dagangan BTC_USD di Bitfinex Exchange digunakan.

import requests
import json

resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

Format data adalah seperti berikut:

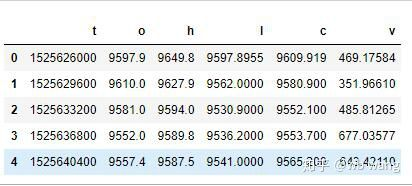
Pemprosesan pra data

df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.

Hanya untuk demonstrasi, anda boleh menggunakan standardisasi data seperti kadar pulangan.

Sediakan data latihan

seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

Bentuk akhir train_x dan train_y ialah: torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). Kerana model kami meramalkan harga penutupan tempoh seterusnya berdasarkan data 10 tempoh, terdapat 800 kumpulan secara teori, selagi terdapat 800 harga penutupan yang diramalkan. Tetapi train_y dalam setiap kumpulan mempunyai 10 data. Sebenarnya, hasil perantara setiap ramalan kumpulan dikekalkan. Apabila mengira kerugian akhir, semua 10 hasil ramalan boleh diambil kira dan dibandingkan dengan nilai sebenar dalam train_y. Secara teori, kita boleh mengira kerugian hasil ramalan terakhir sahaja. Kerana model LSTM tidak mengandungi parameter seq_lenful sebenarnya, maka model ini boleh digunakan untuk pelbagai panjang, dan hasil ramalan di tengah juga bermakna, jadi saya lebih suka menggabungkan dan mengira kerugian.

Perhatikan bahawa ketika menyediakan data latihan, pergerakan tetingkap melompat, dan data yang sudah digunakan tidak lagi digunakan. Sudah tentu, tetingkap juga boleh dipindahkan satu demi satu, sehingga set latihan yang diperoleh jauh lebih besar. Walau bagaimanapun, saya merasakan bahawa data kumpulan bersebelahan terlalu berulang, jadi saya menggunakan kaedah semasa.

6. Membina model LSTM

Model akhir dibina seperti berikut, yang mengandungi LSTM dua lapisan dan lapisan Linear.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.

    def forward(self, x):
        x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.

7. Mula melatih model

Akhirnya kita mula latihan, kod adalah seperti berikut:

criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
    out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # Reverse propagation losses
    optimizer.step() # Update parameters
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

Hasil latihan adalah seperti berikut:

8. Penilaian Model

Nilai ramalan model:

p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

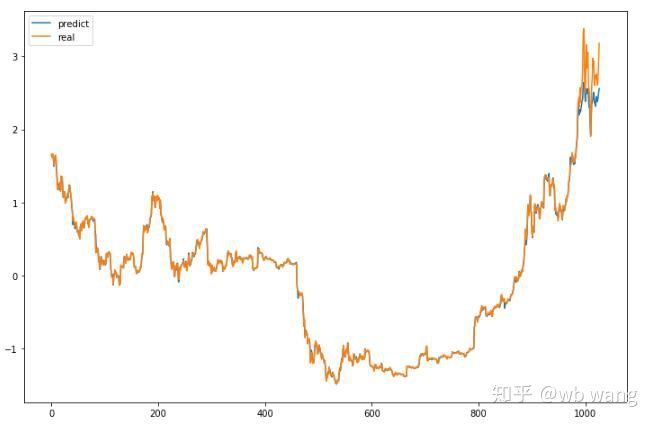
Ia dapat dilihat dari carta bahawa data latihan (sebelum 800) sangat konsisten, tetapi harga Bitcoin telah meningkat pada tempoh kemudian. Model tidak melihat data ini, jadi ramalan tidak mencukupi. Ini juga menunjukkan bahawa terdapat masalah dalam standardisasi data. Walaupun harga yang diramalkan mungkin tidak tepat, apakah ketepatan ramalan kenaikan dan penurunan? Ambil segmen data ramalan untuk melihat:

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

Hasilnya, kadar ketepatan ramalan kenaikan dan kejatuhan mencapai 81.4%, yang masih melebihi jangkaan saya.

Sudah tentu, model ini tidak boleh digunakan untuk bot sebenar, tetapi ia adalah mudah dan mudah difahami. hanya bermula dengan ia. seterusnya, akan ada lebih banyak kursus pengenalan aplikasi rangkaian saraf dalam kuantifikasi mata wang digital.