Redes Neurais e Currency Digital Quantitative Trading Series (1) - LSTM Prevê o preço do Bitcoin
Autora:FMZ~Lydia, Criado: 2023-01-12 13:55:01, Atualizado: 2024-12-19 21:12:23
Redes Neurais e Currency Digital Quantitative Trading Series (1) - LSTM Prevê o preço do Bitcoin
1. Breve introdução
A rede neural profunda tornou-se cada vez mais popular nos últimos anos. Resolveu os problemas que não podiam ser resolvidos no passado em muitos campos e demonstrou sua forte capacidade. Na previsão de séries temporais, o preço da rede neural comumente usado é RNN, porque ele não tem apenas entrada de dados atual, mas também entrada de dados históricos. Claro, quando falamos de previsão de preço RNN, muitas vezes falamos de um dos RNN: LSTM. Este artigo construirá um modelo para prever o preço do Bitcoin com base no PyTorch. Embora haja muitas informações relevantes na Internet, ainda não é completa o suficiente, e há relativamente poucas pessoas que usam o PyTorch. Ainda é necessário escrever um artigo final. O resultado final é usar o preço de abertura, preço de fechamento, preço de negociação mais alto, preço mais baixo e volume de fechamento do Bitcoin para prever o próximo preço. Meu conhecimento pessoal das redes neurais é limitado, espero que suas críticas e correções sejam limitadas. Este tutorial é produzido pela plataforma FMZ Quant Trading (www.fmz.comBem-vindo ao grupo QQ: 863946592 para comunicação.
2. Dados e referências
Dados de preço do Bitcoin provenientes da plataforma de negociação FMZ Quant:https://www.quantinfo.com/Tools/View/4.html- Não. Um exemplo relacionado de previsão de preços:https://yq.aliyun.com/articles/538484- Não. Introdução detalhada ao modelo RNN:https://zhuanlan.zhihu.com/p/27485750- Não. Compreensão da entrada e saída do RNN:https://www.zhihu.com/question/41949741/answer/318771336- Não. Sobre o pytorch: a documentação oficial:https://pytorch.org/docsPara outras informações, pode pesquisar sozinho. Além disso, você precisa de algum conhecimento prévio para ler este artigo, como pandas/python/processamento de dados, mas não importa se você não tem.
Parâmetros do modelo LSTM pytorch
Parâmetros do LSTM:
A primeira vez que vi estes parâmetros densos no documento, a minha reação foi:
Enquanto lia devagar, finalmente entendi.

input_sizeSe o preço de fechamento for previsto pelo preço de fechamento, então input_size=1; Se o preço de fechamento for previsto por alta abertura e baixa fechadura, então input_size=4.hidden_size: Tamanho implícito da camadanum_layers: Número de camadas de RNN.batch_first: Se for verdade, a primeira dimensão de entrada é batch_size, que também é muito confuso, e será descrito em detalhes abaixo.
Introduza os parâmetros dos dados:
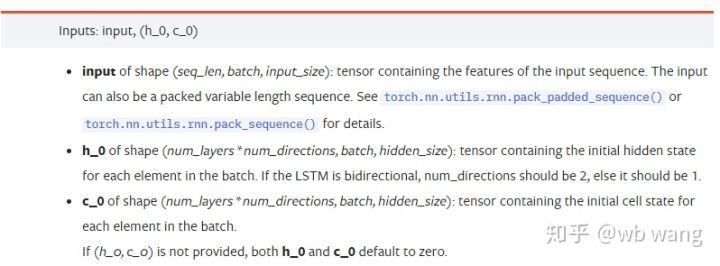
input: Os dados de entrada específicos são um tensor tridimensional, e a forma específica é: (seq_len, batch, input_size). Onde, seq_len refere-se ao comprimento da sequência, ou seja, quanto tempo o LSTM precisa considerar os dados históricos. Observe que isso se refere apenas ao formato dos dados, não à estrutura interna do LSTM. O mesmo modelo LSTM pode inserir diferentes dados seqs_lenh_0: estado oculto inicial, forma como (num_layers * num_directions, batch, hidden_size), se for uma rede bidirecional, num_directions=2.c_0: O estado inicial da célula, a forma como acima, pode não ser especificado.
Parâmetros de saída:
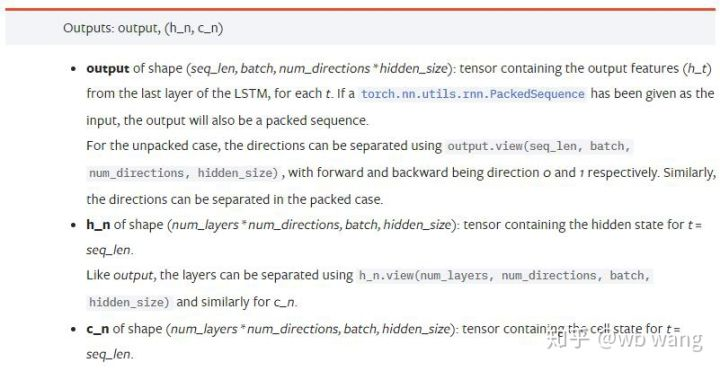
output: A forma da saída (seq_len, batch, num_directions * hidden_size), observe que está relacionada com o parâmetro do modelo batch_first.h_n: O estado h no momento de t = seq_len, mesma forma que h_0.c_n: O estado c no momento de t = seq_len, mesma forma que c_0.
4. Um exemplo simples de entrada e saída LSTM
Importe primeiro o pacote necessário
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
Definir o modelo LSTM
LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)
Preparar os dados de entrada
x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657, 1.4398, -0.3479, 0.2685, 1.6903],
[ 1.0738, 0.6283, -1.3682, -0.1002, -1.7200],
[ 0.2836, 0.3013, -0.3373, -0.3271, 0.0375],
[-0.8852, 1.8098, -1.7099, -0.5992, -0.1143]],
[[ 0.6970, 0.6124, -0.1679, 0.8537, -0.1116],
[ 0.1997, -0.1041, -0.4871, 0.8724, 1.2750],
[ 1.9647, -0.3489, 0.7340, 1.3713, 0.3762],
[ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],
[[-0.5309, 0.1540, -0.4613, -0.6425, -0.1957],
[-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
[-0.4453, 0.1987, -1.0775, 1.3212, 1.3577],
[-0.5488, 0.6669, -0.2151, 0.9337, -1.1805]]])
A forma de x é (3,4,5), porque nós definimosbatch_first=Trueanteriormente, o tamanho do batch_size neste momento é 3, sqe_len é 4, input_size é 5. X [0] representa o primeiro lote.
Se batch_first não for definido, o valor padrão é Falso, então a representação de dados é completamente diferente neste momento. O tamanho do lote é 4, sqe_len é 3, input_size é 5. Neste momento, x [0] representa os dados de todos os lotes quando t = 0, e assim por diante. Eu sinto que essa configuração não é intuitiva, então adicionei o parâmetrobatch_first=True.
A conversão de dados entre os dois também é muito conveniente:x.permute (1,0,2)
Input e output
A forma de entrada e saída de LSTM é muito confusa, e a seguinte figura pode nos ajudar a entender:
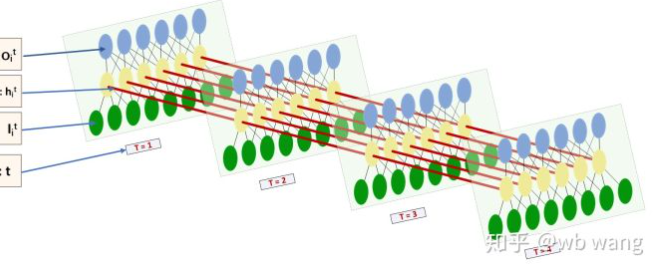
De:https://www.zhihu.com/question/41949741/answer/318771336.
x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])
Observe o resultado de saída, que é consistente com a interpretação do parâmetro anterior. Observe que o segundo valor de hn.size() é 3, que é consistente com o tamanho de batch_size, o que significa que o estado intermediário não é salvo em hn, apenas o último passo é salvo. Uma vez que nossa rede LSTM tem duas camadas, na verdade, a saída da última camada de hn é o valor da saída.
hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]
5. Prepare dados do mercado Bitcoin
É muito importante entender a entrada e saída do LSTM. Caso contrário, é fácil cometer erros extraindo aleatoriamente alguns códigos da Internet. Devido à forte capacidade do LSTM em séries temporais, mesmo que o modelo esteja errado, bons resultados podem ser obtidos no final.
Aquisição de dados
Os dados de mercado do par de negociação BTC_USD na Bitfinex Exchange são utilizados.
import requests
import json
resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
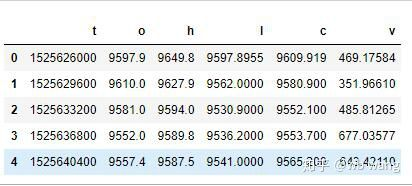
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))
O formato dos dados é o seguinte:
Preprocessamento de dados
df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.
O método de padronização de dados é muito áspero, e haverá alguns problemas.
Preparação dos dados de formação
seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
dataX, dataY=[], []
for i in range(0,len(data)-seq_len, seq_len):
dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
dataY.append(data['n'][i:i+seq_len].values)
return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))
As formas finais de train_x e train_y são: torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). Como nosso modelo prevê o preço de fechamento do próximo período com base nos dados de 10 períodos, há 800 lotes em teoria, desde que haja 800 preços de fechamento previstos. Mas train_y em cada lote tem 10 dados. Na verdade, o resultado intermediário de cada previsão de lote é reservado. Ao calcular a perda final, todos os 10 resultados da previsão podem ser levados em conta e comparados com o valor real em train_y. Teoricamente, podemos calcular a perda apenas do resultado da última previsão. Como o modelo LSTM não contém o parâmetro seq_lenful, o modelo pode ser aplicado a diferentes comprimentos, e os resultados da previsão no meio também são significativos, então prefiro combinar e calcular a perda.
Observe que, ao preparar os dados de treinamento, o movimento da janela está saltando, e os dados já usados não são mais usados. É claro que a janela também pode ser movida um por um, de modo que o conjunto de treinamento obtido seja muito maior. No entanto, senti que os dados de lote adjacentes eram muito repetitivos, então adoti o método atual.
6. Construir o modelo LSTM
O modelo final é construído da seguinte forma, contendo uma camada LSTM de duas camadas e uma camada linear.
class LSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
super(LSTM, self).__init__()
self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.
def forward(self, x):
x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
x = self.reg(x)
return x
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.
7. Comece a treinar o modelo
Finalmente começamos o treino, o código é o seguinte:
criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
loss = criterion(out, train_y)
optimizer.zero_grad()
loss.backward() # Reverse propagation losses
optimizer.step() # Update parameters
print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))
Os resultados da formação são os seguintes:
8. Avaliação do modelo
Valor previsto do modelo:
p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()
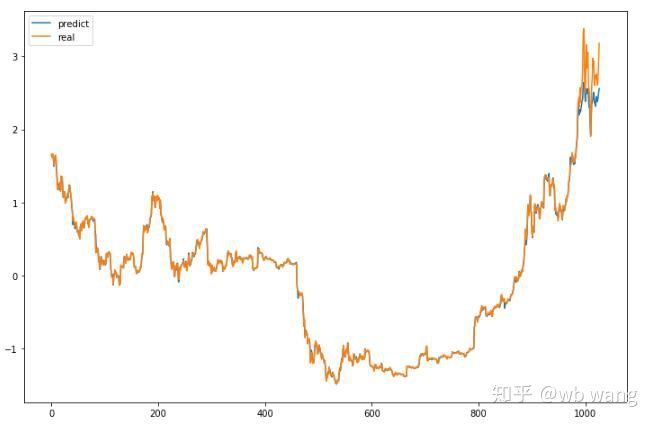
Pode-se ver no gráfico que os dados de treinamento (antes de 800) são muito consistentes, mas o preço do Bitcoin aumentou no período posterior. O modelo não viu esses dados, portanto a previsão é inadequada. Isso também mostra que há problemas na padronização dos dados. Embora o preço previsto possa não ser preciso, qual é a precisão da previsão do aumento e da diminuição?
r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))
Como resultado, a taxa de exatidão da previsão da subida e queda atingiu 81,4%, o que ainda excedeu as minhas expectativas.
Claro, este modelo não é aplicável ao bot real, mas é simples e fácil de entender. Basta começar com ele. Em seguida, haverá mais cursos introdutórios de aplicação de rede neural na quantificação de moeda digital.
- Introdução à arbitragem de lead-lag em criptomoedas (2)
- Introdução ao suporte de Lead-Lag na moeda digital (2)
- Discussão sobre a recepção de sinais externos da plataforma FMZ: uma solução completa para receber sinais com serviço HTTP em estratégia
- Discussão da recepção de sinais externos da plataforma FMZ: estratégias para o sistema completo de recepção de sinais do serviço HTTP embutido
- Introdução à arbitragem de lead-lag em criptomoedas (1)
- Introdução ao suporte de Lead-Lag na moeda digital
- Discussão sobre a recepção de sinais externos da plataforma FMZ: API estendida VS estratégia Serviço HTTP integrado
- Exploração da recepção de sinais externos da plataforma FMZ: API de extensão vs estratégia de serviços HTTP embutidos
- Discussão sobre o método de teste de estratégia baseado no gerador de tickers aleatórios
- Métodos de teste de estratégias baseados em geradores de mercado aleatórios
- Novo recurso do FMZ Quant: Use a função _Serve para criar serviços HTTP facilmente
- Sistema de negociação intradiário de ponto pivô
- 6 estratégias e práticas simples para iniciantes em negociação quantitativa de moeda digital
- Quadro estratégico do intervalo verdadeiro médio
- Prática e aplicação da estratégia do termostato na plataforma FMZ Quant
- Estratégia de negociação baseada na teoria da caixa, apoiando futuros de commodities e moeda digital
- Estratégia quantitativa de negociação baseada no preço
- Estratégia quantitativa de negociação utilizando um índice ponderado pelo volume de negociação
- Implementação e aplicação da estratégia de negociação PBX na plataforma de negociação FMZ Quant
- Compartilhamento tardio: Bitcoin robô de alta frequência com 5% de retornos diários em 2014
- Redes neurais e negociação quantitativa de moeda digital série (2) - Aprendizagem e treinamento intensivos estratégia de negociação Bitcoin
- Aplicação da estratégia combinada do índice de força relativa da SMA e do índice de força relativa do RSI
- Desenvolvimento da estratégia CTA e da biblioteca de classes padrão da plataforma FMZ Quant
- Estratégia de negociação quantitativa com análise de dinâmica de preços em Python
- Implementar uma estratégia de negociação quantitativa de moeda digital de duplo impulso em Python
- A melhor maneira de instalar e atualizar para Linux docker
- Realização de estratégias equitativas equilibradas de posições longas-cortas com um alinhamento ordenado
- Análise de dados de séries temporais e backtesting de dados de tiques
- Análise Quantitativa do Mercado de Moeda Digital
- Negociação em pares baseada em tecnologia baseada em dados
- Aplicação da Tecnologia de Aprendizagem de Máquina no Comércio