Нейронные сети и цифровая валюта Количественная серия торговли (1) - LSTM предсказывает цену Биткоина

Нейронные сети и цифровая валюта Количественная серия торговли (1) - LSTM предсказывает цену Биткоина

1. Краткое введение

Глубокая нейронная сеть стала все более и более популярной в последние годы. Она решила проблемы, которые не могли быть решены в прошлом во многих областях, и продемонстрировала свою сильную способность. В прогнозировании временных рядов обычно используемой цены нейронной сети является RNN, потому что она имеет не только текущий вход данных, но и исторический вход данных. Конечно, когда мы говорим о прогнозировании цены RNN, мы часто говорим об одном из RNN: LSTM. Эта статья будет строить модель для прогнозирования цены Bitcoin на основе PyTorch. Хотя в Интернете есть много релевантной информации, она все еще недостаточно тщательна, и относительно мало людей, использующих PyTorch. Все еще необходимо написать статью. Конечным результатом является использование цены открытия, закрытия, самой высокой цены торговли, самой низкой цены и объема закрытия Bitcoin для прогнозирования следующей цены. Я надеюсь на ваши личные знания и критику и кор Это руководство создано платформой FMZ Quant Trading (www.fmz.comДобро пожаловать в группу QQ: 863946592 для общения.

2. Данные и ссылки

Данные о ценах на биткоин получены на платформе FMZ Quant Trading:https://www.quantinfo.com/Tools/View/4.html- Да, конечно. Соответствующий пример прогнозирования цен:https://yq.aliyun.com/articles/538484- Да, конечно. Подробное введение в модель RNN:https://zhuanlan.zhihu.com/p/27485750- Да, конечно. Понимание ввода и вывода RNN:https://www.zhihu.com/question/41949741/answer/318771336- Да, конечно. О питорче: официальная документация:https://pytorch.org/docsДля получения другой информации, вы можете искать самостоятельно. Кроме того, для чтения этой статьи вам нужны предварительные знания, например, о пандах/питоне/обработке данных, но это не имеет значения, если вы этого не знаете.

3. Параметры модели LSTM питорча

Параметры LSTM:

Когда я впервые увидел эти плотные параметры на документе, моя реакция была: "Что это, черт возьми, такое?"

Читая медленно, я наконец-то понял.

input_size: Введите характерный размер вектора x. Если цена закрытия предсказана ценой закрытия, то input_size=1; Если цена закрытия предсказана высоким открытием и низким закрытием, то input_size=4.hidden_size: Имплицитный размер слояnum_layers: Количество слоев РНН.batch_first: Если это верно, первое измерение ввода batch_size, которое также очень запутанно, и оно будет подробно описано ниже.

Введите параметры данных:

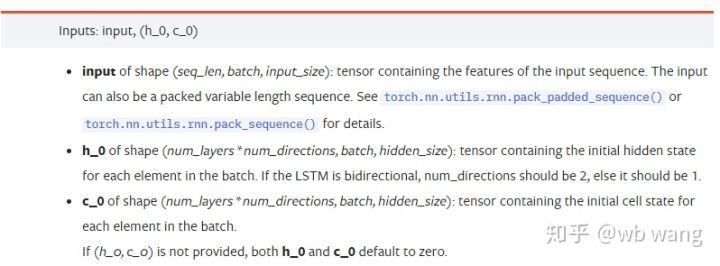
input: Конкретные входные данные представляют собой трехмерный тензор, а конкретная форма: (seq_len, batch, input_size). Где, seq_len относится к длине последовательности, то есть сколько времени LSTM должен рассматривать исторические данные. Обратите внимание, что это относится только к формату данных, а не к внутренней структуре LSTM. Одна и та же модель LSTM может вводить различные данные seqs_lens, которые могут давать результаты прогноза; batch относится к размеру партии, представляющей количество различных групп данных; input_size является предыдущим input_size.h_0: Первоначальное скрытое состояние, форма как (num_layers * num_directions, batch, hidden_size), если это двусторонняя сеть, num_directions=2.c_0: Начальное состояние ячейки, форма, как выше, может быть неопределенной.

Выходные параметры:

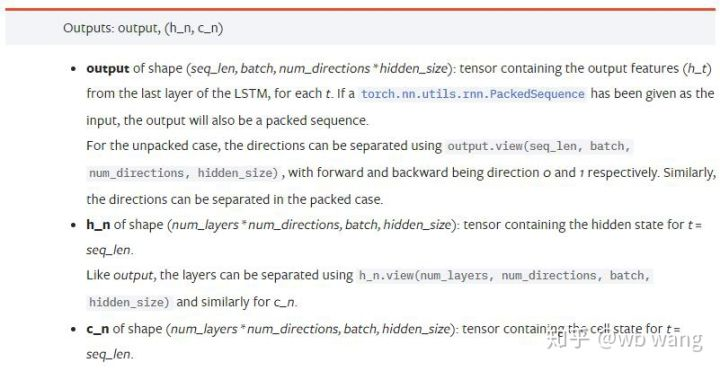
output: Форма вывода (seq_len, batch, num_directions * hidden_size), обратите внимание, что он связан с параметром модели batch_first.h_n: Состояние h в момент t = seq_len, такая же форма, как h_0.c_n: Состояние c в момент t = seq_len, такая же форма, как c_0.

4. Простой пример ввода и вывода LSTM

Сначала импортируйте необходимый пакет

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

Определить модель LSTM

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

Подготовить входные данные

x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

Форма х (3,4,5), потому что мы определилиbatch_first=Trueранее, размер batch_size на данный момент 3, sqe_len 4, input_size 5. X [0] представляет первую партию.

Если batch_first не определено, значение по умолчанию False, то представление данных совершенно другое в это время. Размер партии 4, sqe_len 3, input_size 5. В это время x [0] представляет данные всех партий, когда t = 0, и так далее. Я чувствую, что эта настройка не интуитивно понятна, поэтому я добавил параметрbatch_first=True.

Конверсия данных между ними также очень удобна:x.permute (1,0,2)

Вход и выход

Форма ввода и вывода LSTM очень запутанна, и следующая цифра может помочь нам понять:

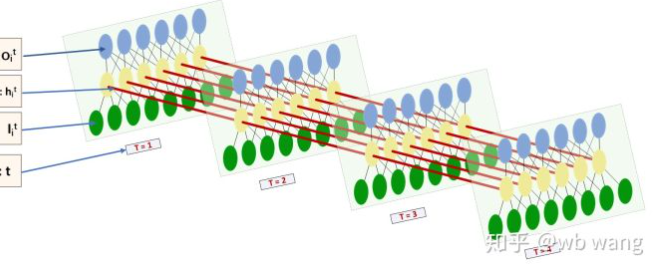
От:https://www.zhihu.com/question/41949741/answer/318771336.

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

Обратите внимание, что второе значение hn.size (()) равняется 3, что соответствует размеру batch_size, что означает, что промежуточное состояние не сохраняется в hn, сохраняется только последний шаг. Поскольку наша сеть LSTM имеет два слоя, фактически выход последнего слоя hn - это значение выхода. Форма выхода [3, 4, 10], которая сохраняет результаты во все времена t = 0,1,2,3, так:

hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. Подготовить данные рынка биткойнов

Так много было сказано раньше, что является только прелюдией. Очень важно понять вход и выход LSTM. В противном случае легко совершить ошибки, случайным образом извлекая некоторые коды из Интернета. Из-за сильной способности LSTM в временных рядах, даже если модель неверна, в конце концов можно получить хорошие результаты.

Получение данных

Используются рыночные данные торговой пары BTC_USD на бирже Bitfinex.

import requests
import json

resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

Формат данных следующий:

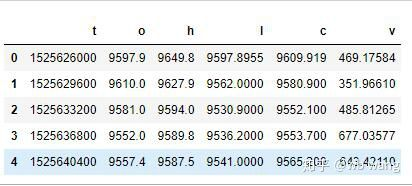
Предварительная обработка данных

df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.

Метод стандартизации данных очень грубый, и будут некоторые проблемы.

Подготовить данные по обучению

seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

Окончательные формы train_x и train_y: torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). Поскольку наша модель предсказывает цену закрытия следующего периода на основе данных 10 периодов, теоретически существует 800 партий, пока существует 800 прогнозируемых цен на закрытие. Но train_y в каждой партии имеет 10 данных. На самом деле промежуточный результат каждого предсказания партии зарезервирован. При расчете окончательной потери все 10 результатов прогноза можно принять во внимание и сравнить с фактическим значением в train_y. Теоретически мы можем рассчитать потерю только последнего результата прогноза. Поскольку модель LSTM на самом деле не содержит параметра seq_lenful, поэтому модель может быть применена к разным длинам, а результаты прогноза в середине также имеют смысл, поэтому я предпочитаю комбинировать и рассчитывать потерю.

Обратите внимание, что при подготовке тренировочных данных движение окна перескакивает, и уже использованные данные больше не используются. Конечно, окно также можно перемещать одно за другим, так что полученный набор тренировок намного больше. Однако я почувствовал, что соседние партии данных слишком повторяются, поэтому я принял текущий метод.

6. Создать модель LSTM

Окончательная модель построена следующим образом, содержащая двухслойный LSTM и линейный слой.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.

    def forward(self, x):
        x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.

7. Начните обучать модель

Наконец мы начинаем тренировку, код следующий:

criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
    out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # Reverse propagation losses
    optimizer.step() # Update parameters
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

Результаты обучения следующие:

8. Оценка модели

Прогнозируемое значение модели:

p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

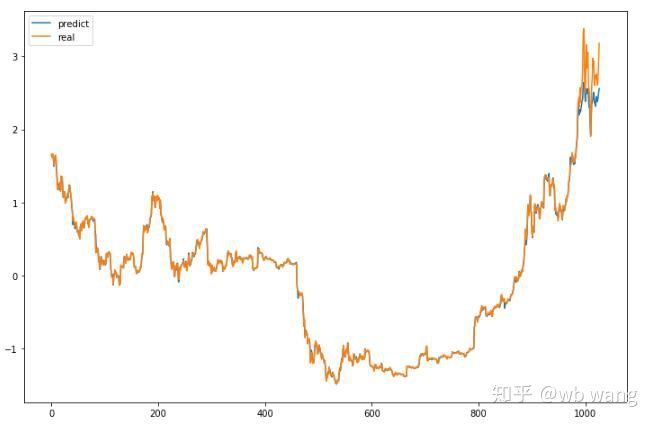
Из диаграммы можно увидеть, что данные о тренировках (до 800) очень последовательны, но цена биткойна выросла в более поздний период. Модель не видела этих данных, поэтому прогноз неадекватный. Это также показывает, что есть проблемы в стандартизации данных. Хотя прогнозируемая цена может быть неточной, какая точность прогноза роста и снижения?

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

В результате точность прогнозирования роста и падения достигла 81,4%, что все еще превышает мои ожидания.

Конечно, эта модель не применима к реальному боту, но она проста и легко понятна. Просто начните с нее. Далее, будут более вводные курсы применения нейронных сетей в количественной цифровой валюте.