پچھلے مضمون (https://www.fmz.com/digest-topic/4187) میں، ہم نے جوڑوں کی تجارت کی حکمت عملی متعارف کروائی تھی اور تجارتی حکمت عملیوں کو بنانے اور خودکار بنانے کے لیے ڈیٹا اور ریاضیاتی تجزیہ کو استعمال کرنے کا طریقہ دکھایا تھا۔

طویل مدتی متوازن ایکویٹی حکمت عملی تجارتی اہداف کی ٹوکری پر لاگو جوڑے کی تجارت کی حکمت عملی کا قدرتی توسیع ہے۔ یہ خاص طور پر بہت سی قسموں اور باہمی تعلقات کے ساتھ تجارتی منڈیوں کے لیے موزوں ہے، جیسے ڈیجیٹل کرنسی مارکیٹ اور کموڈٹی فیوچر مارکیٹ۔

بنیادی اصول

طویل مدتی متوازن ایکویٹی حکمت عملی ایک ہی وقت میں تجارتی اہداف کی ایک ٹوکری پر طویل اور مختصر جانا ہے۔ جوڑے کی تجارت کی طرح، یہ طے کریں کہ کون سے سرمایہ کاری کے اہداف سستے ہیں اور کون سے مہنگے ہیں۔ اس کے بعد درجہ بندی کی بنیاد پر سب سے اوپر n سرمایہ کاری پر لمبا چلے گا، اور برابر رقم کے ساتھ نچلے حصے میں n سرمایہ کاری (لمبی پوزیشنوں کی کل قیمت = مختصر پوزیشنوں کی کل قیمت)۔

یاد رکھیں پہلے جب ہم نے کہا تھا کہ جوڑوں کی تجارت مارکیٹ کی غیر جانبدار حکمت عملی ہے؟ طویل مدتی متوازن ایکویٹی حکمت عملی کے لیے بھی یہی بات درست ہے، کیونکہ طویل اور مختصر پوزیشنوں کی مساوی مقدار اس بات کو یقینی بناتی ہے کہ حکمت عملی مارکیٹ غیر جانبدار رہے گی (مارکیٹ کے اتار چڑھاو سے متاثر نہیں ہوگی)۔ حکمت عملی اعدادوشمار کے لحاظ سے بھی مضبوط ہے؛ سرمایہ کاری کی درجہ بندی کرکے اور متعدد پوزیشنیں لے کر، آپ اپنے درجہ بندی کے ماڈل کو صرف ایک بار کے خطرے کی نمائش کے لیے بے نقاب کر سکتے ہیں۔ آپ جس چیز پر شرط لگا رہے ہیں وہ آپ کی درجہ بندی کی اسکیم کا معیار ہے۔

درجہ بندی کی اسکیم کیا ہے؟

رینکنگ اسکیم ایک ایسا ماڈل ہے جو ہر سرمایہ کاری کے ہدف کو اس کی متوقع کارکردگی کی بنیاد پر ترجیح دیتا ہے۔ عوامل قدر کے عوامل، تکنیکی اشارے، قیمتوں کا تعین کرنے والے ماڈل یا مندرجہ بالا تمام چیزوں کا مجموعہ ہو سکتے ہیں۔ مثال کے طور پر، آپ رجحان کی پیروی کرنے والی سرمایہ کاری کی فہرست کی درجہ بندی کرنے کے لیے مومینٹم میٹرک کا استعمال کر سکتے ہیں: سب سے زیادہ رفتار والی سرمایہ کاری سے اچھی کارکردگی جاری رکھنے کی توقع کی جائے گی اور کم سے کم رفتار والی سرمایہ کاری سب سے زیادہ خراب کارکردگی کا مظاہرہ کرے گی۔ سب سے کم منافع ہے.

اس حکمت عملی کی کامیابی کا انحصار تقریباً مکمل طور پر استعمال کی جانے والی رینکنگ اسکیم پر ہے، یعنی آپ کی رینکنگ اسکیم اعلی کارکردگی والی سرمایہ کاری کو کم کارکردگی والی سرمایہ کاری سے الگ کرنے کے قابل ہے، اور طویل مدتی سرمایہ کاری کے ہدف کی حکمت عملی کے منافع کو بہتر طریقے سے سمجھتی ہے۔ اس لیے درجہ بندی کی اسکیم تیار کرنا بہت ضروری ہے۔

درجہ بندی کا منصوبہ کیسے بنایا جائے؟

ایک بار جب ہمارے پاس ایک درجہ بندی کی اسکیم ہے، تو ہم ظاہر ہے کہ اس سے فائدہ اٹھانا چاہتے ہیں۔ ہم یہ سب سے اوپر کی درجہ بندی کی سرمایہ کاری کو طویل کرنے اور نیچے کی درجہ بندی کی سرمایہ کاری کو مختصر کرنے کے لیے اتنی ہی رقم لگا کر کرتے ہیں۔ یہ اس بات کو یقینی بناتا ہے کہ حکمت عملی صرف اس کی درجہ بندی کے معیار کے تناسب سے پیسہ کمائے گی اور “مارکیٹ غیر جانبدار” ہوگی۔

فرض کریں کہ آپ تمام سرمایہ کاری کو m کی درجہ بندی کر رہے ہیں، آپ کے پاس سرمایہ کاری کے لیے n ڈالر ہیں، اور آپ کل 2p (جہاں m>2p) پوزیشنز رکھنا چاہتے ہیں۔ اگر درجہ 1 کے ساتھ سرمایہ کاری سے بدترین کارکردگی کی توقع کی جاتی ہے، تو درجہ m والی سرمایہ کاری سے بہترین کارکردگی کی توقع کی جاتی ہے:

• آپ سرمایہ کاری کے اہداف کو اس طرح ترتیب دیتے ہیں: 1، …، p، اور مختصر 2/2p USD سرمایہ کاری کے اہداف

• آپ سرمایہ کاری کے اہداف کو اس طرح ترتیب دیتے ہیں: m-p,……,m، اور سرمایہ کاری کے اہداف کے n/2p ڈالر پر طویل سفر کریں۔

نوٹس:چونکہ قیمت میں اضافے کی وجہ سے ہدف کی قیمت ہمیشہ n/2p کو یکساں طور پر تقسیم نہیں کرے گی، اور کچھ اہداف کو عدد میں خریدنا ضروری ہے، اس لیے کچھ غیر درست الگورتھم ہوں گے، اور الگورتھم اس نمبر کے جتنا ممکن ہو قریب ہونا چاہیے۔ n = 100000 اور p = 500 کے ساتھ چلنے والی حکمت عملی کے لیے، ہم دیکھتے ہیں:

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

یہ 100 سے زیادہ فرکشن والی قیمتوں کے لیے بڑی پریشانیوں کا سبب بن سکتا ہے (جیسے کموڈٹی فیوچر مارکیٹس)، کیونکہ آپ فرکشنل قیمتوں کے ساتھ پوزیشن نہیں کھول سکتے (یہ مسئلہ کرپٹو کرنسی مارکیٹ میں موجود نہیں ہے)۔ ہم فرکشنل پرائس ٹریڈز کو کم کرکے یا سرمائے میں اضافہ کرکے اس کو کم کرتے ہیں۔

آئیے ایک فرضی مثال کو دیکھتے ہیں۔

• موجد مقداری پلیٹ فارم پر اپنے تحقیقی ماحول کی تعمیر

سب سے پہلے، ہموار طریقے سے کام کرنے کے لیے، ہمیں اپنے تحقیقی ماحول کو بنانے کی ضرورت ہے، اس مضمون میں، ہم تحقیقی ماحول کو بنانے کے لیے Inventor Quantitative Platform (FMZ.COM) کا استعمال کرتے ہیں، بنیادی طور پر تاکہ ہم آسان اور تیز API کا استعمال کر سکیں۔ بعد میں اس پلیٹ فارم کا انٹرفیس اور انکیپسولیشن مکمل ڈوکر سسٹم۔

موجد کوانٹیٹیو پلیٹ فارم کے آفیشل نام پر، اس ڈوکر سسٹم کو میزبان سسٹم کہا جاتا ہے۔

میزبانوں اور روبوٹس کو تعینات کرنے کے طریقے کے بارے میں مزید معلومات کے لیے، براہ کرم میرا سابقہ ​​مضمون دیکھیں: https://www.fmz.com/bbs-topic/4140

وہ قارئین جو اپنا کلاؤڈ کمپیوٹنگ سرور تعیناتی میزبان خریدنا چاہتے ہیں اس مضمون کا حوالہ دے سکتے ہیں: https://www.fmz.com/bbs-topic/2848

کلاؤڈ کمپیوٹنگ سروس اور ہوسٹ سسٹم کو کامیابی کے ساتھ تعینات کرنے کے بعد، ہم سب سے طاقتور Python ٹول انسٹال کریں گے: ایناکونڈا

اس مضمون کے لیے درکار تمام متعلقہ پروگرام ماحول کو حاصل کرنے کے لیے (انحصار لائبریریاں، ورژن کا انتظام، وغیرہ)، سب سے آسان طریقہ ایناکونڈا کا استعمال ہے۔ یہ ایک پیکڈ Python ڈیٹا سائنس ایکو سسٹم اور انحصار مینیجر ہے۔

ایناکونڈا کی تنصیب کے طریقہ کار کے لیے، براہ کرم ایناکونڈا کے آفیشل گائیڈ سے رجوع کریں: https://www.anaconda.com/distribution/

اس مضمون میں Python سائنسی کمپیوٹنگ میں دو بہت مشہور اور اہم لائبریریوں Numpy اور pandas کا بھی استعمال کیا جائے گا۔

مندرجہ بالا بنیادی کام کے لیے، آپ میرے پچھلے مضمون کو بھی دیکھ سکتے ہیں، جس میں بتایا گیا ہے کہ ایناکونڈا ماحول اور دو لائبریریوں کو کیسے ترتیب دیا جائے، تفصیلات کے لیے، براہ کرم دیکھیں: https://www.fmz.com/digest-۔ موضوع/4169

ہم بے ترتیب سرمایہ کاری اور بے ترتیب عوامل پیدا کرتے ہیں اور ان کی درجہ بندی کرتے ہیں۔ آئیے فرض کریں کہ ہماری مستقبل کی واپسی دراصل ان فیکٹر ویلیوز پر منحصر ہے۔

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

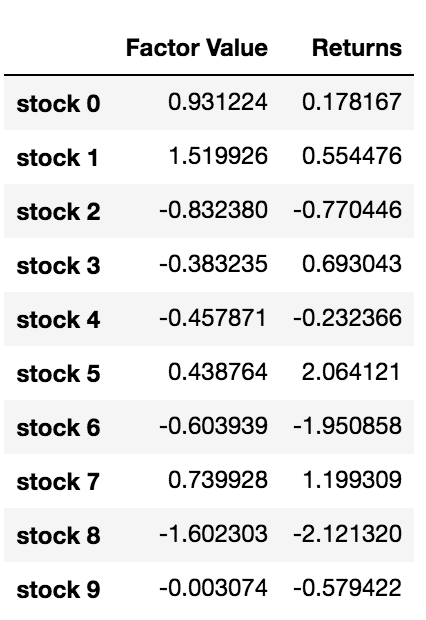
اب جب کہ ہمارے پاس فیکٹر ویلیوز اور ریٹرن ہیں، ہم دیکھ سکتے ہیں کہ کیا ہوتا ہے اگر ہم فیکٹر ویلیوز کی بنیاد پر سرمایہ کاری کی درجہ بندی کریں اور پھر لمبی اور مختصر پوزیشنیں کھولیں۔

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

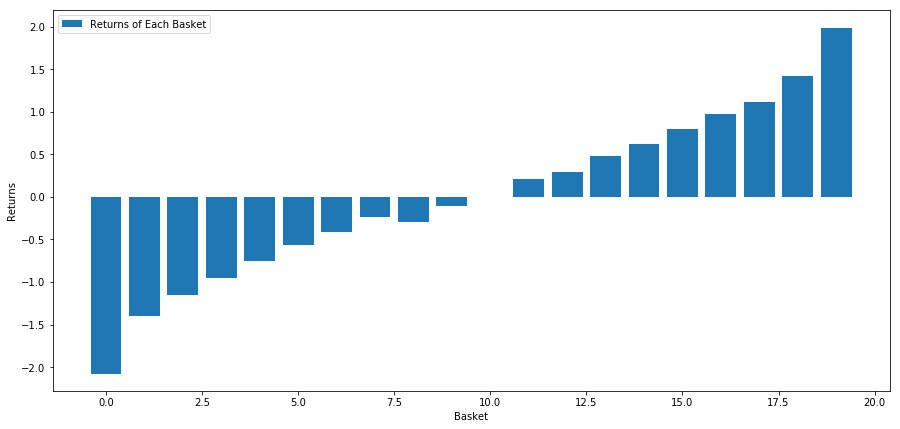
ہماری حکمت عملی سرمایہ کاری کے اہداف کی ایک ٹوکری میں پہلی درجہ کی سرمایہ کاری پر طویل اور دسویں درجے کی سرمایہ کاری کے ہدف کو مختصر کرنا ہے۔ اس حکمت عملی کے انعامات یہ ہیں:

basket_returns[number_of_baskets-1] - basket_returns[0]

نتیجہ ہے: 4.172

اعلی کارکردگی والی سرمایہ کاری کو کم کارکردگی والی سرمایہ کاری سے الگ کرنے کے لیے اپنے پیسے ہمارے رینکنگ ماڈل پر لگائیں۔

اس مضمون کے بقیہ حصے میں، ہم درجہ بندی کی اسکیموں کا جائزہ لینے کے طریقہ پر تبادلہ خیال کرتے ہیں۔ درجہ بندی پر مبنی ثالثی سے پیسہ کمانے کا فائدہ یہ ہے کہ یہ مارکیٹ کی خرابی سے متاثر نہیں ہوتا ہے، بلکہ اس سے فائدہ اٹھا سکتا ہے۔

آئیے ایک حقیقی دنیا کی مثال پر غور کریں۔

ہم S&P 500 میں مختلف شعبوں کے 32 اسٹاکس کا ڈیٹا لوڈ کرتے ہیں اور ان کی درجہ بندی کرنے کی کوشش کرتے ہیں۔

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

آئیے درجہ بندی کی بنیاد کے طور پر ایک ماہ کی مدت میں نارملائزڈ مومنٹم انڈیکیٹر کا استعمال کریں۔

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

اب ہم اپنے سٹاک کے رویے کا تجزیہ کریں گے اور دیکھیں گے کہ ہمارا سٹاک ہمارے منتخب کردہ درجہ بندی کے عوامل کے اندر مارکیٹ میں کیسا کارکردگی دکھاتا ہے۔

ڈیٹا کا تجزیہ کریں۔

اسٹاک کا برتاؤ

آئیے اس پر ایک نظر ڈالتے ہیں کہ ہماری منتخب کردہ اسٹاک کی ٹوکری ہمارے درجہ بندی کے ماڈل میں کیسی کارکردگی کا مظاہرہ کرتی ہے۔ ایسا کرنے کے لیے، آئیے تمام اسٹاکس کے لیے ایک ہفتے کے آگے کے منافع کا حساب لگائیں۔ اس کے بعد ہم 30 دن کی رفتار کے ساتھ ہر اسٹاک کے 1 ہفتہ کے آگے کی واپسی کے باہمی تعلق کو دیکھ سکتے ہیں۔ وہ اسٹاک جو مثبت ارتباط کو ظاہر کرتے ہیں وہ مندرجہ ذیل رجحان ہیں، اور وہ اسٹاک جو منفی ارتباط ظاہر کرتے ہیں ان کا مطلب ہے واپس جانا۔

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

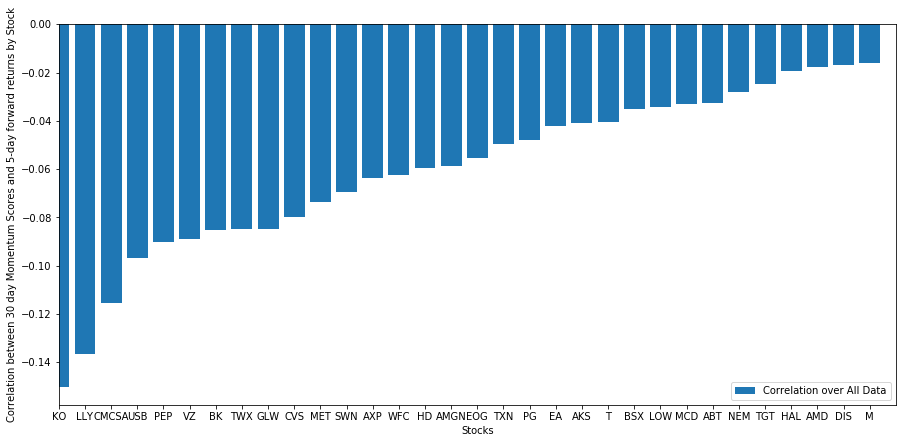
ہمارے تمام اسٹاک کا مطلب کسی حد تک واپس جانا ہے! (بظاہر ہماری منتخب کائنات اس طرح کام کرتی ہے) یہ ہمیں بتاتا ہے کہ اگر کوئی اسٹاک مومینٹم تجزیہ پر بہت زیادہ درجہ رکھتا ہے، تو ہمیں اگلے ہفتے اس سے کم کارکردگی کی توقع کرنی چاہیے۔

مومینٹم سکور رینکنگ اور ریٹرن کے درمیان ارتباط

اس کے بعد، ہمیں اپنے رینکنگ سکور اور مارکیٹ کے مجموعی فارورڈ ریٹرن کے درمیان تعلق کو دیکھنے کی ضرورت ہے، یعنی متوقع منافع کی پیشین گوئی اور ہمارے درجہ بندی کے عوامل کے درمیان تعلق کیا اعلیٰ ارتباط کی سطح غریب رشتہ دار واپسی کی پیشین گوئی کر سکتی ہے، یا اس کے برعکس؟

ایسا کرنے کے لیے، ہم تمام اسٹاکس کے لیے 30 دن کی رفتار اور 1 ہفتے کے فارورڈ ریٹرن کے درمیان روزانہ کے ارتباط کا حساب لگاتے ہیں۔

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

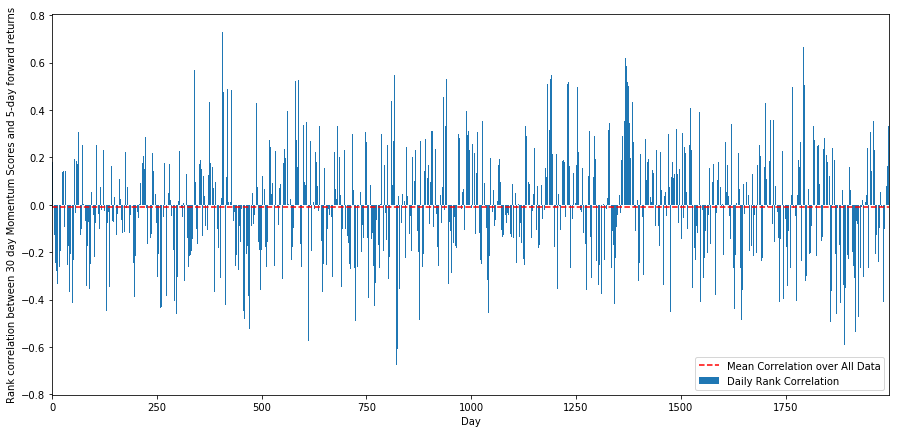
روزانہ کا ارتباط کافی شور والا ہے، لیکن بہت معمولی ہے (جس کی توقع ہے کیونکہ ہم نے کہا ہے کہ تمام اسٹاک کا مطلب ہے واپسی)۔ ہم 1 ماہ کے فارورڈ ریٹرن کے اوسط ماہانہ ارتباط کو بھی دیکھتے ہیں۔

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

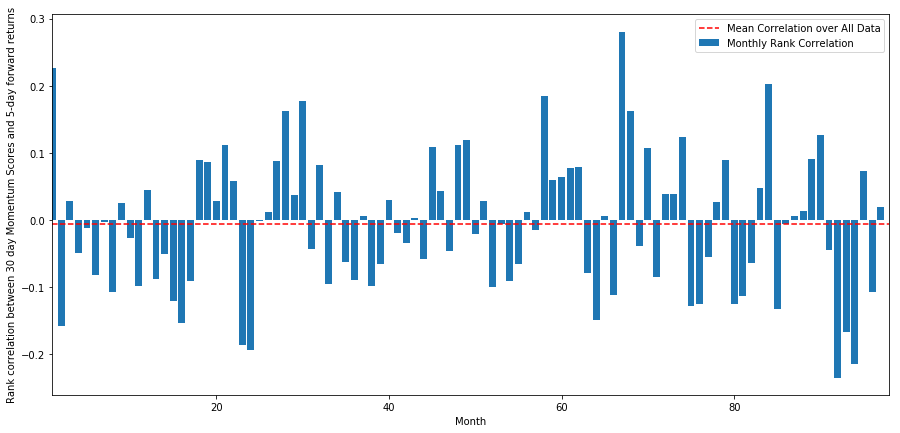
ہم دیکھ سکتے ہیں کہ اوسط ارتباط دوبارہ تھوڑا سا منفی ہے، لیکن مہینے سے مہینے میں بہت زیادہ مختلف ہوتا ہے.

اوسط اسٹاک ٹوکری واپسی

ہم نے اپنی درجہ بندی سے لیے گئے اسٹاک کی ایک ٹوکری کے لیے منافع کا حساب لگایا ہے۔ اگر ہم تمام اسٹاکس کی درجہ بندی کریں اور پھر انہیں n گروپوں میں تقسیم کریں تو ہر گروپ کی اوسط واپسی کیا ہوگی؟

پہلا قدم ایک ایسا فنکشن بنانا ہے جو ہر ماہ دی جانے والی ہر ٹوکری کے لیے اوسط واپسی اور درجہ بندی کا عنصر دے گا۔

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

اس سکور کی بنیاد پر اسٹاک کی درجہ بندی کرتے وقت ہم ہر ٹوکری کی اوسط واپسی کا حساب لگاتے ہیں۔ اس سے ہمیں طویل عرصے تک ان کے تعلقات کا اچھا اندازہ ہونا چاہیے۔

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

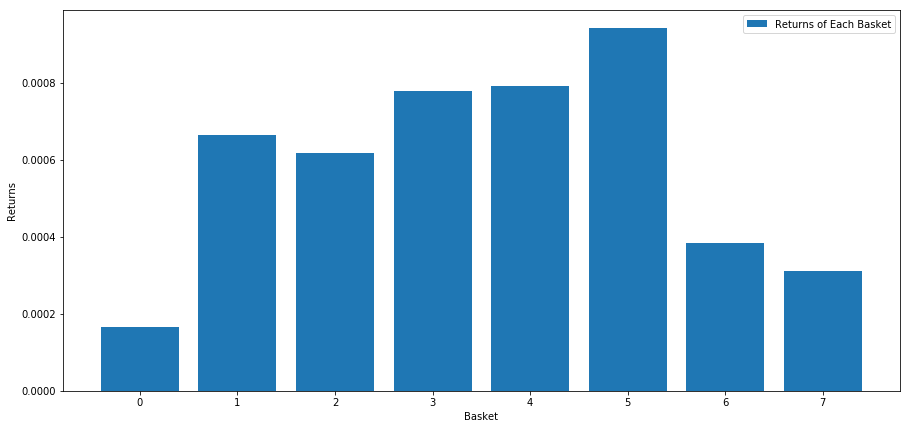
ایسا لگتا ہے کہ ہم اعلی اداکاروں کو کم اداکاروں سے الگ کرنے کے قابل ہیں۔

پھیلاؤ (بنیاد) مستقل مزاجی

یقینا، یہ صرف اوسط تعلقات ہیں. یہ سمجھنے کے لیے کہ یہ رشتہ کتنا مستقل ہے اور کیا ہم کوئی معاہدہ کرنے کے لیے تیار ہیں، ہمیں وقت کے ساتھ ساتھ اس کے بارے میں اپنا نقطہ نظر اور رویہ بدلنا چاہیے۔ اگلا، ہم پچھلے دو سالوں کے لیے ان کے ماہانہ اسپریڈز (بنیاد) کو دیکھیں گے۔ ہم مزید تبدیلیاں دیکھ سکتے ہیں اور یہ تعین کرنے کے لیے مزید تجزیہ کر سکتے ہیں کہ آیا یہ مومینٹم سکور قابل تجارت ہے۔

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

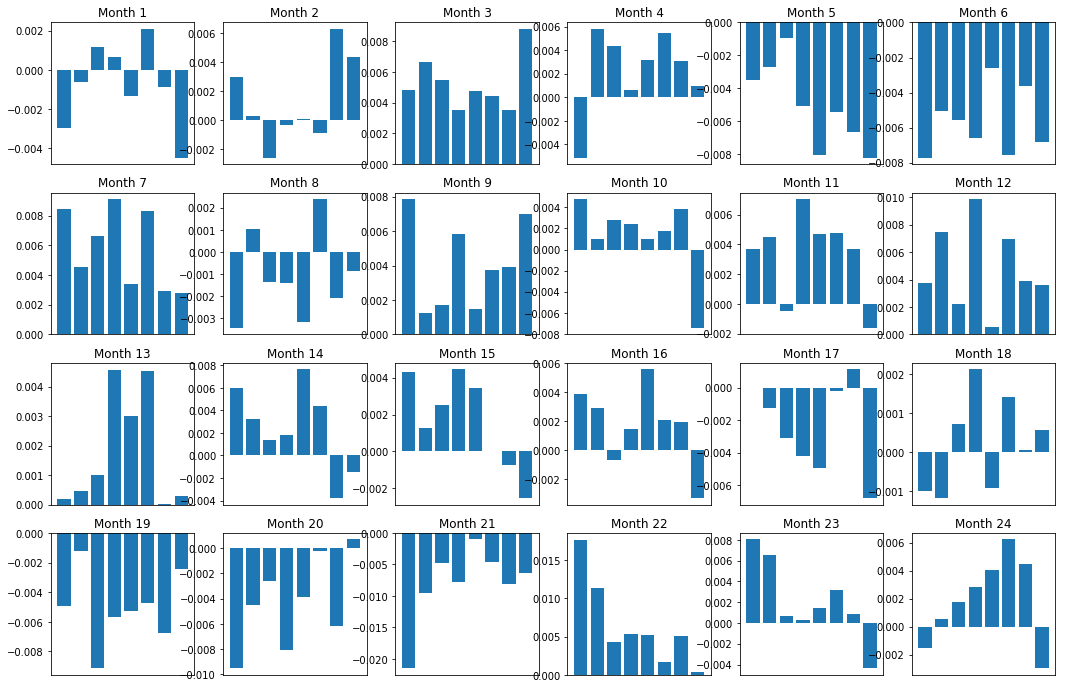
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

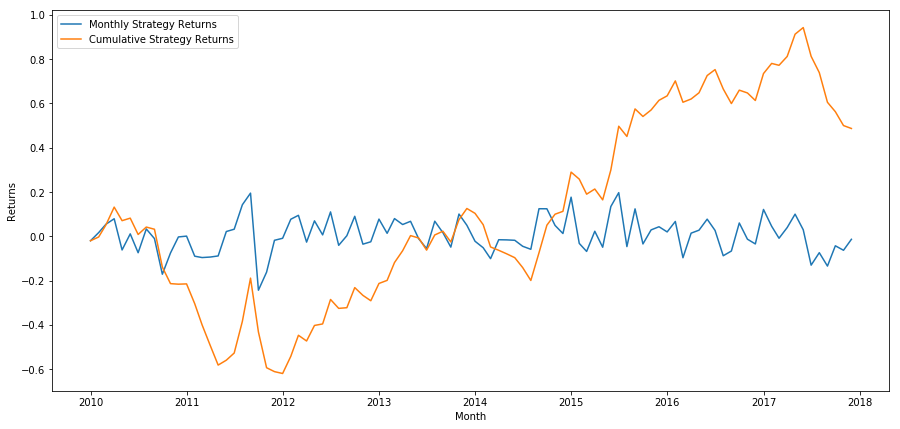
آخر میں، آئیے واپسی پر نظر ڈالیں اگر ہم آخری ٹوکری طویل اور ہر ماہ پہلی ٹوکری کو مختصر کرتے ہیں (ہر سیکیورٹی کے لیے مساوی سرمایہ مختص کرتے ہوئے)

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

سالانہ واپسی: 5.03%

ہم دیکھتے ہیں کہ ہمارے پاس ایک بہت کمزور درجہ بندی کی اسکیم ہے جو صرف اعلی کارکردگی والے اسٹاک کو کم کارکردگی والے اسٹاک سے ممتاز کرتی ہے۔ مزید برآں، اس درجہ بندی کی اسکیم میں کوئی مستقل مزاجی نہیں ہے اور یہ ہر ماہ بڑے پیمانے پر مختلف ہوتی رہتی ہے۔

صحیح درجہ بندی کی اسکیم تلاش کرنا

طویل مدتی متوازن ایکویٹی حکمت عملی کو نافذ کرنے کے لیے، آپ کو واقعی صرف درجہ بندی کی اسکیم کا تعین کرنے کی ضرورت ہے۔ اس کے بعد سب کچھ مکینیکل ہے۔ ایک بار جب آپ کے پاس طویل مدتی متوازن ایکویٹی حکمت عملی ہو جائے تو، آپ بہت کچھ تبدیل کیے بغیر درجہ بندی کے مختلف عوامل میں تبادلہ کر سکتے ہیں۔ ہر بار پورے کوڈ کو درست کرنے کی فکر کیے بغیر اپنے خیالات پر تیزی سے اعادہ کرنے کا یہ ایک بہت ہی آسان طریقہ ہے۔

درجہ بندی کی اسکیم تقریبا کسی بھی ماڈل سے بھی آ سکتی ہے۔ اس کا قدر پر مبنی فیکٹر ماڈل ہونا ضروری نہیں ہے، یہ ایک مشین لرننگ تکنیک ہو سکتی ہے جو ایک ماہ قبل واپسی کی پیش گوئی کرتی ہے اور اس کی بنیاد پر ان کی درجہ بندی کرتی ہے۔

درجہ بندی کی اسکیموں کا انتخاب اور تشخیص

درجہ بندی کی اسکیم طویل مدتی متوازن ایکویٹی حکمت عملی کا فائدہ ہے اور یہ سب سے اہم جزو بھی ہے۔ ایک اچھی درجہ بندی کی اسکیم کا انتخاب ایک منظم منصوبہ ہے اور اس کے کوئی آسان جواب نہیں ہیں۔

ایک اچھا نقطہ آغاز یہ ہے کہ موجودہ معلوم ٹیکنالوجیز کو چنیں اور دیکھیں کہ کیا آپ زیادہ منافع حاصل کرنے کے لیے ان میں قدرے ترمیم کر سکتے ہیں۔ ہم یہاں کچھ ابتدائی نکات پر بات کریں گے:

• کلون کریں اور ایڈجسٹ کریں۔: کوئی ایسی چیز چنیں جس پر اکثر بحث کی جاتی ہو اور دیکھیں کہ کیا آپ اپنے فائدے کے لیے اس میں تھوڑی سی ترمیم کر سکتے ہیں۔ عام طور پر، عوامی عوامل کے پاس اب تجارتی سگنل نہیں ہوں گے کیونکہ وہ پوری طرح سے مارکیٹ سے باہر ہو چکے ہیں۔ تاہم، بعض اوقات وہ آپ کو صحیح سمت میں لے جا سکتے ہیں۔

• قیمتوں کا تعین کرنے والا ماڈل: کوئی بھی ماڈل جو مستقبل کے منافع کی پیشن گوئی کرتا ہے ایک عنصر ہو سکتا ہے اور اس میں آپ کے تجارتی اہداف کی ٹوکری کی درجہ بندی کرنے کے لیے استعمال ہونے کی صلاحیت ہے۔ آپ قیمتوں کا کوئی بھی پیچیدہ ماڈل لے سکتے ہیں اور اسے درجہ بندی کی اسکیم میں تبدیل کر سکتے ہیں۔

• قیمت پر مبنی عوامل (تکنیکی اشارے): قیمت پر مبنی عوامل، جیسا کہ آج ہم نے بحث کی ہے، ہر ایکویٹی کی تاریخی قیمت کے بارے میں معلومات لیں اور اسے فیکٹر ویلیو بنانے کے لیے استعمال کریں۔ مثالیں حرکت پذیر اوسط اشارے، رفتار کے اشارے یا اتار چڑھاؤ کے اشارے ہوسکتے ہیں۔

• رجعت اور رفتار: یہ بات قابل غور ہے کہ کچھ عوامل کا خیال ہے کہ ایک بار جب قیمتیں ایک سمت میں چلی جائیں گی تو وہ ایسا کرتی رہیں گی۔ کچھ عوامل بالکل برعکس ہیں۔ دونوں مختلف ٹائم فریموں اور اثاثوں پر درست ماڈل ہیں، اور یہ مطالعہ کرنا ضروری ہے کہ آیا بنیادی رویہ رفتار ہے یا رجعت پر مبنی ہے۔

• بنیادی عوامل (قدر کی بنیاد پر): یہ بنیادی اقدار جیسے PE، ڈیویڈنڈز وغیرہ کا مجموعہ استعمال کر رہا ہے۔ بنیادی قدر کسی کمپنی کے بارے میں حقیقی دنیا کے حقائق سے متعلق معلومات پر مشتمل ہوتی ہے اور اس وجہ سے کئی طریقوں سے قیمت سے زیادہ طاقتور ہو سکتی ہے۔

بالآخر، پیشین گوئی کرنے والوں کو تیار کرنا ہتھیاروں کی دوڑ ہے جہاں آپ ایک قدم آگے رہنے کی کوشش کر رہے ہیں۔ عوامل مارکیٹ سے باہر ہوتے ہیں اور ان کی عمر ہوتی ہے، اس لیے آپ کو یہ تعین کرنے کے لیے مسلسل کام کرنا چاہیے کہ آپ کے عوامل کو کس قدر زوال کا سامنا ہے اور ان کی جگہ لینے کے لیے کون سے نئے عوامل استعمال کیے جا سکتے ہیں۔

دیگر تحفظات

• تعدد کو دوبارہ متوازن کرنا

ہر درجہ بندی کا نظام قدرے مختلف ٹائم فریم میں واپسی کی پیش گوئی کرتا ہے۔ قیمت پر مبنی اوسط تبدیلی کچھ دنوں میں پیشین گوئی ہو سکتی ہے، جبکہ قدر پر مبنی فیکٹر ماڈل چند مہینوں کے دوران پیش گوئی کر سکتے ہیں۔ وقت کے افق کا تعین کرنا بہت ضروری ہے کہ ماڈل کو حکمت عملی کو عملی جامہ پہنانے سے پہلے اعدادوشمار کے لحاظ سے اس کی پیشن گوئی اور توثیق کرنی چاہیے۔ آپ یقینی طور پر اپنی ری بیلنسنگ فریکوئنسی کو بہتر بنانے کی کوشش کر کے زیادہ فٹ نہیں ہونا چاہتے ہیں؛ آپ کو لامحالہ ایک ایسا مل جائے گا جو آپ کی رینکنگ سکیم کی پیش گوئی کے وقت کے افق کا تعین کر لے، اس کے لیے تقریباً اس فریکوئنسی کو دوبارہ متوازن کرنے کی کوشش کریں۔ اپنے ماڈل سے زیادہ سے زیادہ فائدہ اٹھائیں۔

• سرمایہ کی صلاحیت اور لین دین کے اخراجات

ہر حکمت عملی میں کم سے کم اور زیادہ سے زیادہ سرمائے کی ضرورت ہوتی ہے، جس میں کم از کم حد عام طور پر لین دین کی لاگت سے متعین ہوتی ہے۔

بہت زیادہ اسٹاک کی تجارت کے نتیجے میں لین دین کے اخراجات زیادہ ہوں گے۔ فرض کریں کہ آپ 1,000 شیئرز خریدنا چاہتے ہیں، ہر ایک ری بیلنسنگ پر کئی ہزار ڈالر لاگت آئے گی۔ آپ کے سرمائے کی بنیاد کافی زیادہ ہونی چاہیے تاکہ لین دین کے اخراجات آپ کی حکمت عملی کے ذریعے پیدا ہونے والے منافع کے ایک چھوٹے سے حصے کی نمائندگی کریں۔ مثال کے طور پر، اگر آپ کا سرمایہ \(100,000 ہے اور آپ کی حکمت عملی ماہانہ 1% (\)1000) کماتی ہے، تو یہ تمام واپسی لین دین کی لاگت سے کھا جائے گی۔ 1,000 سے زیادہ شیئرز پر منافع حاصل کرنے کے لیے اس حکمت عملی کو چلانے کے لیے آپ کو لاکھوں ڈالر کے سرمائے کی ضرورت ہوگی۔

کم از کم اثاثہ کی حد کا انحصار بنیادی طور پر تجارت شدہ اسٹاک کی تعداد پر ہوتا ہے۔ تاہم، زیادہ سے زیادہ صلاحیت بھی بہت زیادہ ہے، اور طویل مدتی متوازن ایکویٹی حکمت عملی اپنا کنارہ کھوئے بغیر سیکڑوں ملین ڈالر کی تجارت کرنے کے قابل ہے۔ یہ درست ہے کیونکہ حکمت عملی نسبتاً کبھی کبھار ہی متوازن ہوتی ہے جو کہ خریدے گئے حصص کی تعداد سے تقسیم ہونے سے فی حصص بہت کم ڈالر کی قیمت ملے گی، اور آپ کو اپنے تجارتی حجم کے بارے میں فکر کرنے کی ضرورت نہیں ہے۔ فرض کریں کہ آپ 1,000 حصص کی تجارت کرتے ہیں، یہ \(100,000,000 ہے۔ اگر آپ نے ہر ماہ اپنے پورے پورٹ فولیو میں توازن پیدا کیا، تو آپ فی سٹاک صرف \)100,000 فی مہینہ ٹریڈنگ کر رہے ہوں گے، جو زیادہ تر سیکیورٹیز کے لیے اہم مارکیٹ شیئر ہونے کے لیے کافی نہیں ہے۔