Mô hình hóa và phân tích biến động Bitcoin dựa trên mô hình ARMA-EGARCH

Gần đây, tôi đã phân tích về sự biến động của Bitcoin, nó rất nhiều từ và tự phát. Vì vậy, tôi chỉ đơn giản chia sẻ một số hiểu biết và mã của mình như sau. Khả năng của tôi bị giới hạn, và mã không hoàn hảo. Nếu có bất kỳ lỗi nào, vui lòng chỉ ra và sửa chữa trực tiếp.

1. Một mô tả ngắn gọn về chuỗi thời gian tài chính

Dòng thời gian tài chính là một tập hợp các mô hình chuỗi quá trình Stochastic dựa trên một biến được quan sát trong chiều dài thời gian. biến này thường là tỷ lệ lợi nhuận của tài sản. Bởi vì tỷ lệ lợi nhuận độc lập với quy mô đầu tư và có tính chất thống kê, nó có giá trị hơn để phân tích các cơ hội đầu tư của tài sản tài chính cơ bản.

Ở đây, nó được giả định mạnh mẽ rằng tỷ lệ lợi nhuận của Bitcoin phù hợp với các đặc điểm tỷ lệ lợi nhuận của các tài sản tài chính chung, tức là, nó là một chuỗi mượt mà yếu, có thể được chứng minh bằng cách kiểm tra tính nhất quán của một số mẫu.

Đồ chuẩn bị, thư viện nhập khẩu, chức năng đóng gói

Cấu hình của môi trường nghiên cứu đã hoàn tất. Thư viện cần thiết cho các tính toán tiếp theo được nhập vào đây. Vì nó được viết gián đoạn, nó có thể là dư thừa. Vui lòng tự dọn dẹp nó.

Trong [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Ra khỏi [1]: {Chỉ số: 10000.0, FrozenBalance: 0.0, Stock: 0.0, FrozenStock: 0.0}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

Trong [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

1-2. Hãy bắt đầu với một sự hiểu biết ngắn gọn về dữ liệu lịch sử của Bitcoin

Từ quan điểm thống kê, chúng ta có thể xem xét một số đặc điểm dữ liệu của Bitcoin. Bằng cách lấy mô tả dữ liệu của năm qua làm ví dụ, tỷ lệ lợi nhuận được tính theo cách đơn giản, tức là giá đóng được trừ logaritm. Công thức như sau: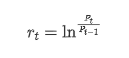

Trong [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Ra khỏi [1]: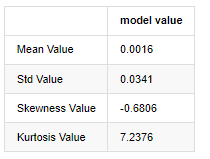

Tính năng của đuôi mỡ dày là thời gian ngắn hơn, tính năng càng quan trọng. Kurtosis sẽ tăng lên với tần số dữ liệu tăng lên, và tính năng sẽ rất rõ ràng trong dữ liệu tần số cao.

Lấy dữ liệu giá đóng cửa hàng ngày từ ngày 1 tháng 1 năm 2019 đến nay làm ví dụ, chúng tôi phân tích mô tả tỷ lệ lợi nhuận logaritm của nó, và có thể thấy rằng chuỗi tỷ lệ lợi nhuận đơn giản của Bitcoin không phù hợp với sự phân bố bình thường, và nó có đặc điểm rõ ràng của đuôi béo dày.

Giá trị trung bình của chuỗi là 0.0016, độ lệch chuẩn là 0.0341, độ lệch là -0.6819, và kurtosis là 7.2243, cao hơn nhiều so với phân bố bình thường và có đặc điểm đuôi mỡ dày.

Trong [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Ra khỏi [1]:

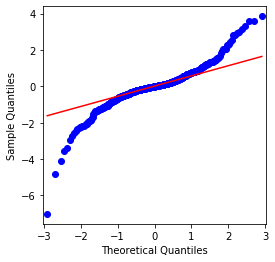
Có thể thấy rằng biểu đồ QQ là hoàn hảo, và chuỗi logaritm cho Bitcoin không phù hợp với phân bố bình thường từ kết quả, và nó có đặc điểm rõ ràng của đuôi mỡ dày.

Tiếp theo, chúng ta hãy xem xét hiệu ứng tổng hợp biến động, nghĩa là các chuỗi thời gian tài chính thường đi kèm với biến động lớn hơn sau biến động lớn hơn, trong khi biến động nhỏ hơn thường được theo sau bởi biến động nhỏ hơn.

Nhóm hóa biến động phản ánh các hiệu ứng phản hồi tích cực và tiêu cực của biến động và nó có mối tương quan cao với các đặc điểm đuôi mỡ.

Trong [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Ra khỏi [5]:

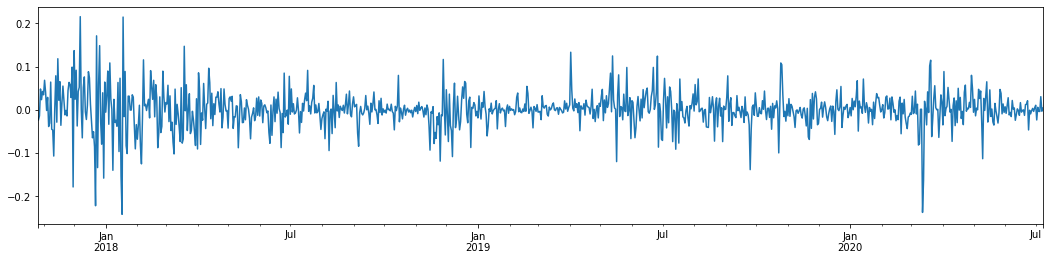
Nếu lấy tỷ lệ lãi suất logaritm hàng ngày của Bitcoin trong 3 năm qua và vẽ ra, hiện tượng nhóm biến động có thể được nhìn thấy rõ ràng. Sau thị trường tăng giá của Bitcoin vào năm 2018, nó đã ở trong một vị trí ổn định trong hầu hết thời gian. Như chúng ta có thể thấy ở bên phải xa, vào tháng 3 năm 2020, khi thị trường tài chính toàn cầu sụp đổ, cũng có một cuộc chạy đua về thanh khoản Bitcoin, với lợi nhuận giảm gần 40% trong một ngày, với những dao động âm tính mạnh.

Nói tóm lại, từ quan sát trực quan, chúng ta có thể thấy rằng một biến động lớn sẽ được theo sau bởi một biến động dày đặc với xác suất lớn, cũng là hiệu ứng tổng hợp của biến động.

1-3. Chuẩn bị dữ liệu

Để chuẩn bị bộ mẫu đào tạo, đầu tiên, chúng tôi thiết lập một mẫu chuẩn, trong đó tỷ lệ lợi nhuận logaritm là tỷ lệ biến động quan sát tương đương. Bởi vì sự biến động của ngày không thể được quan sát trực tiếp, dữ liệu hàng giờ được sử dụng để lấy lại để suy luận sự biến động thực tế của ngày và lấy nó làm biến phụ thuộc của sự biến động.

Phương pháp lấy mẫu lại dựa trên dữ liệu hàng giờ. Công thức được hiển thị như sau: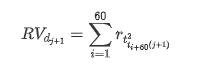

Trong [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Ra khỏi [1]: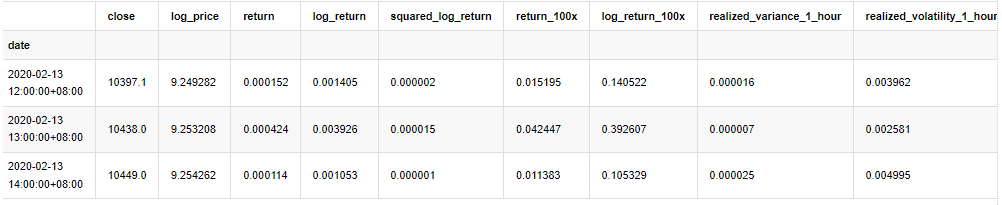

Chuẩn bị dữ liệu bên ngoài mẫu theo cùng một cách

Trong [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

Để hiểu được dữ liệu cơ bản của mẫu, một phân tích mô tả đơn giản được thực hiện như sau:

Trong [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

Ra khỏi[9]:

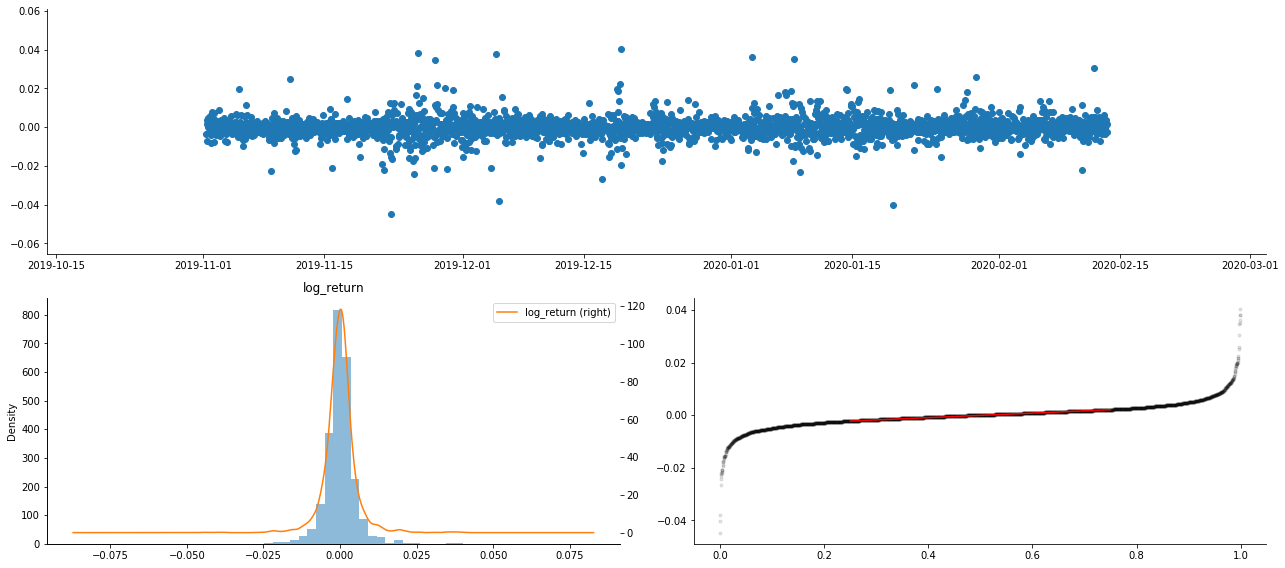
Kết quả là có sự tổng hợp biến động rõ ràng và hiệu ứng đòn bẩy trong biểu đồ chuỗi thời gian của lợi nhuận logarithmic.

Sự lệch trong biểu đồ phân bố các kết quả logaritm nhỏ hơn 0, cho thấy các kết quả trong mẫu là âm và thiên vị sang bên phải một chút.

Độ lệch của sự phân bố dữ liệu là nhỏ hơn 1, cho thấy rằng các kết quả trong mẫu là tích cực nhẹ và có thiên vị bên phải nhẹ. Giá trị kurtosis lớn hơn 3, cho thấy rằng năng suất là đuôi mỡ dày phân phối.

Bây giờ chúng ta đã đạt đến điểm này, hãy làm một bài kiểm tra thống kê khác. Trong [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

Ra ngoài[7]:

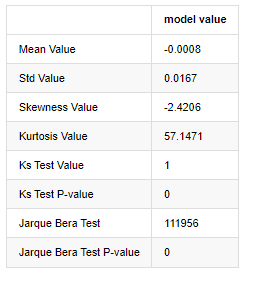
Số liệu thống kê thử nghiệm Kolmogorov - Smirnov và Jarque - Bera được sử dụng tương ứng. Giả thuyết ban đầu được đặc trưng bởi sự khác biệt đáng kể và phân bố bình thường. Nếu giá trị P thấp hơn giá trị quan trọng của mức độ tin cậy 0,05%, giả thuyết ban đầu bị từ chối.

Có thể thấy rằng giá trị kurtosis lớn hơn 3, cho thấy các đặc điểm của đuôi mỡ dày. Các giá trị P của KS và JB nhỏ hơn khoảng cách tin cậy. Giả sử phân bố bình thường bị từ chối, điều này chứng minh rằng tỷ lệ hoàn vốn của BTC không có các đặc điểm của phân bố bình thường, và nghiên cứu thực nghiệm có các đặc điểm của đuôi mỡ dày.

1-4. So sánh biến động thực hiện và biến động quan sát

Chúng ta kết hợp square_log_ return (logarithmic yield square) và realized_variance (realized variance) cho các quan sát.

Trong [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

Ra khỏi [1]:

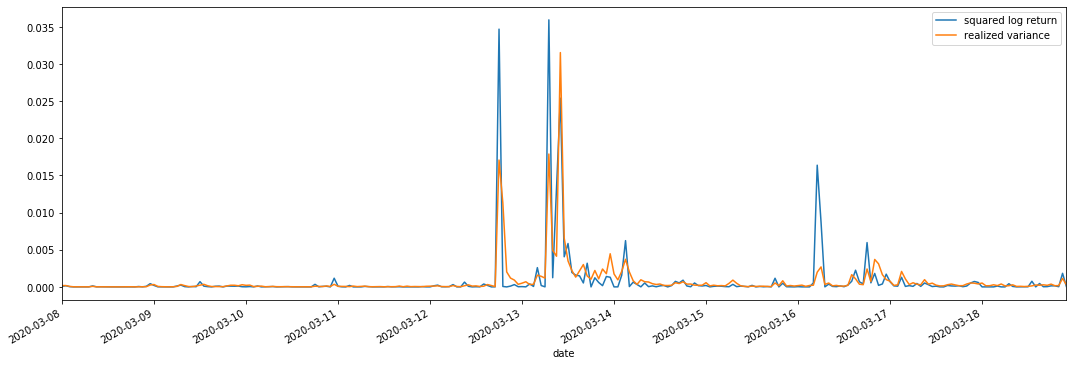
Có thể thấy rằng khi phạm vi biến thể thực hiện lớn hơn, độ biến động của phạm vi tỷ lệ lợi nhuận cũng lớn hơn và tỷ lệ lợi nhuận thực hiện mượt mà hơn.

Từ quan điểm lý thuyết thuần túy, RV gần hơn với biến động thực tế, trong khi biến động ngắn hạn được làm mịn bởi vì biến động trong ngày thuộc về dữ liệu qua đêm, vì vậy từ quan sát, biến động trong ngày phù hợp hơn với thị trường chứng khoán biến động tần suất thấp hơn.

2. Sự trơn tru của chuỗi thời gian

Nếu nó là một chuỗi không tĩnh, nó cần phải được điều chỉnh gần đúng với một chuỗi tĩnh. Cách phổ biến là xử lý khác biệt. Về lý thuyết, sau nhiều lần khác biệt, chuỗi không tĩnh có thể được gần đúng với một chuỗi tĩnh. Nếu sự tương đồng của chuỗi mẫu ổn định, kỳ vọng, sự tương đồng và sự tương đồng của các quan sát của nó sẽ không thay đổi theo thời gian, cho thấy rằng chuỗi mẫu thuận tiện hơn để suy luận trong phân tích thống kê.

Các bài kiểm tra cơ bản đơn vị, cụ thể là thử nghiệm ADF, được sử dụng ở đây. thử nghiệm ADF sử dụng thử nghiệm t để quan sát sự quan trọng. Về nguyên tắc, nếu chuỗi không hiển thị xu hướng rõ ràng, chỉ có các mục không đổi được giữ lại. Nếu chuỗi có xu hướng, phương trình hồi quy nên bao gồm cả các mục không đổi và các mục xu hướng thời gian. Ngoài ra, các tiêu chí AIC và BIC có thể được sử dụng để đánh giá dựa trên các tiêu chí thông tin. Nếu công thức được yêu cầu, nó là như sau: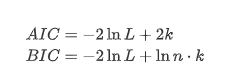

Trong [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

Ra khỏi[8]: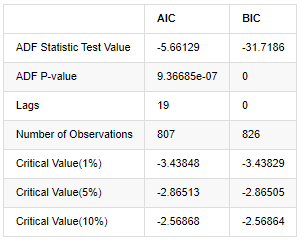

Giả sử ban đầu là không có gốc đơn vị trong chuỗi, nghĩa là, giả định thay thế là chuỗi là tĩnh. Giá trị P của thử nghiệm thấp hơn nhiều so với giá trị cắt giảm mức độ tin cậy 0,05%, từ chối giả định ban đầu, vì vậy tỷ lệ trở lại log là một chuỗi tĩnh, có thể được mô hình hóa bằng cách sử dụng mô hình chuỗi thời gian thống kê.

3. Xác định mô hình và xác định đơn đặt hàng

Để thiết lập phương trình giá trị trung bình, cần phải thực hiện thử nghiệm tương quan tự động trên chuỗi để đảm bảo rằng thuật ngữ lỗi không có tương quan tự động.

Trong [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Ra khỏi [1]:

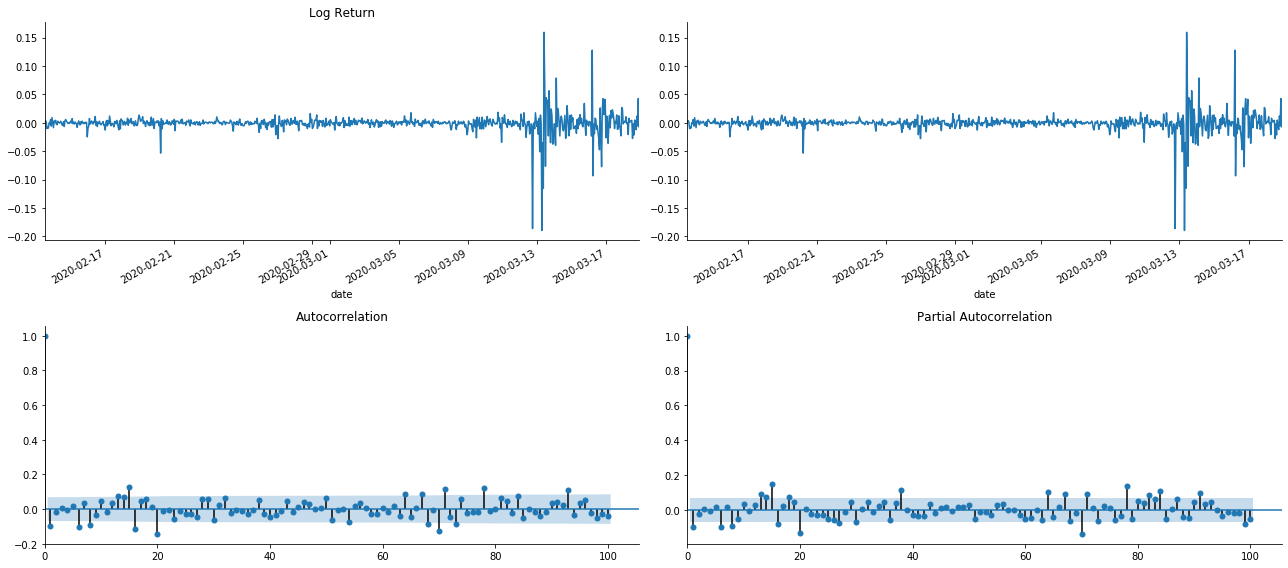
Có thể thấy rằng hiệu ứng cắt ngắn là hoàn hảo. Vào thời điểm đó, hình ảnh này đã truyền cảm hứng cho tôi. Liệu thị trường có thực sự không hợp lệ không? Để xác minh, chúng tôi sẽ thực hiện phân tích tương quan tự động trên chuỗi trả về và xác định thứ tự trễ của mô hình.

Các hệ số tương quan thường được sử dụng là để đo tương quan giữa nó và chính nó, tức là tương quan giữa r ((t) và r (t-l) tại một thời điểm nhất định trong quá khứ: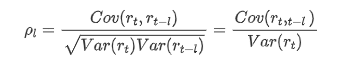

Sau đó, hãy thực hiện một bài kiểm tra định lượng. Giả định ban đầu là tất cả các hệ số tương quan tự động là 0, nghĩa là không có tương quan tự động trong chuỗi. Công thức thống kê thử nghiệm được viết như sau: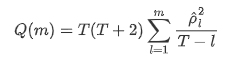

Mười hệ số tương quan tự động được lấy để phân tích, như sau:

Trong [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

Ra khỏi[9]: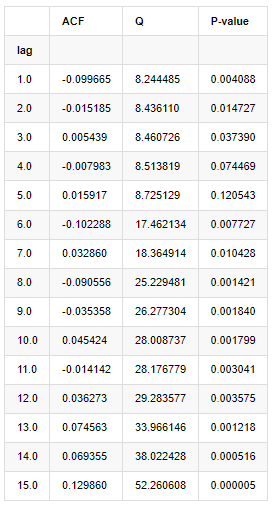

Theo thống kê thử nghiệm Q và giá trị P, chúng ta có thể thấy rằng hàm tự động tương quan ACF dần dần trở thành 0 sau thứ tự 0. Các giá trị P của thống kê thử nghiệm Q đủ nhỏ để bác bỏ giả định ban đầu, do đó có tự động tương quan trong chuỗi.

4. Mô hình ARMA

Các mô hình AR và MA khá đơn giản. Nói một cách đơn giản, Markdown quá mệt mỏi để viết công thức. Nếu bạn quan tâm, vui lòng tự kiểm tra chúng. Mô hình AR (Autoregression) chủ yếu được sử dụng để mô hình chuỗi thời gian. Nếu chuỗi đã vượt qua bài kiểm tra ACF, nghĩa là hệ số tương quan tự với khoảng thời gian 1 là đáng kể, nghĩa là dữ liệu tại thời điểm có thể hữu ích để dự đoán thời gian t.

Mô hình MA (Mức trung bình động) sử dụng sự can thiệp ngẫu nhiên hoặc dự đoán lỗi của các khoảng thời gian q trước để biểu hiện giá trị dự đoán hiện tại tuyến tính.

Để mô tả đầy đủ cấu trúc năng động của dữ liệu, cần phải tăng thứ tự của các mô hình AR hoặc MA, nhưng các tham số như vậy sẽ làm cho tính toán phức tạp hơn.

Vì các chuỗi thời gian giá thường không tĩnh, và tác dụng tối ưu hóa của phương pháp khác biệt đối với tĩnh đã được thảo luận trước đây, mô hình ARIMA (p, d, q) (tổng trung bình di chuyển tự hồi) thêm xử lý khác biệt d-order dựa trên việc áp dụng các mô hình hiện có cho chuỗi. Tuy nhiên, vì chúng tôi đã sử dụng logaritm, chúng tôi có thể sử dụng ARMA (p, q) trực tiếp.

Nói tóm lại, sự khác biệt duy nhất giữa mô hình ARIMA và quá trình xây dựng mô hình ARMA là nếu kết quả không ổn định được thu được sau khi phân tích trạng thái tĩnh, mô hình sẽ thực hiện sự khác biệt bậc hai với chuỗi trực tiếp và sau đó thực hiện thử nghiệm tĩnh, và sau đó xác định thứ tự p và q cho đến khi chuỗi ổn định. Sau khi xây dựng mô hình và đánh giá nó, dự đoán tiếp theo sẽ được thực hiện, loại bỏ bước quay lại để thực hiện sự khác biệt. Tuy nhiên, sự khác biệt giá thứ hai là vô nghĩa, vì vậy ARMA là lựa chọn tốt nhất.

4-1. lựa chọn đơn đặt hàng

Tiếp theo, chúng ta có thể chọn thứ tự trực tiếp theo tiêu chí thông tin, ở đây chúng ta thử nó với các sơ đồ nhiệt động học của AIC và BIC.

Trong [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

Ra khỏi[10]: Param tốt nhất AIC: (0, 1, 1) Param tốt nhất BIC: (0, 1, 1) HQIC param tốt nhất: (0, 1, 1) Param tốt nhất được chọn: (0, 1, 1)

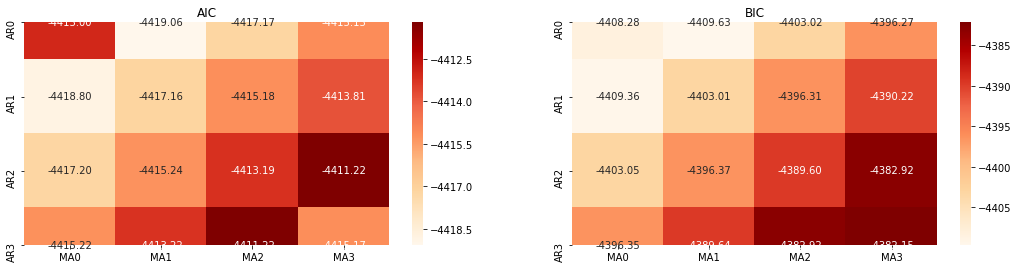
Rõ ràng là sự kết hợp tham số thứ nhất tối ưu cho giá logaritm là (0,1,1), đơn giản và đơn giản. Log_return (tỷ lệ logaritm của lợi nhuận) thực hiện cùng một hoạt động. Giá trị tối ưu AIC là (4,3), và giá trị tối ưu BIC là (0,1). Vì vậy, sự kết hợp tối ưu của các tham số cho log_return (tỷ lệ logaritm của lợi nhuận) là (0,1).

4-2. mô hình ARMA và phù hợp

Các hệ số hàng quý không được yêu cầu, nhưng SARIMAX giàu tính năng hơn, vì vậy nó đã được quyết định chọn mô hình này để mô hình hóa và tình cờ vẽ một phân tích mô tả như sau:

Trong [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

Ra khỏi [1]: Kết quả mô hình không gian nhà nước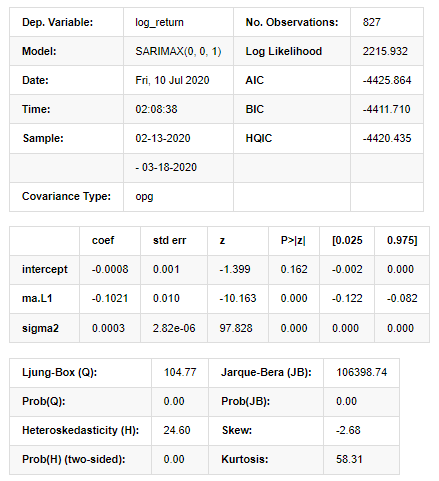

Cảnh báo: [1] Ma trận covariance được tính bằng cách sử dụng sản phẩm bên ngoài của gradient (bước phức tạp). Trong [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Ra khỏi [1]:

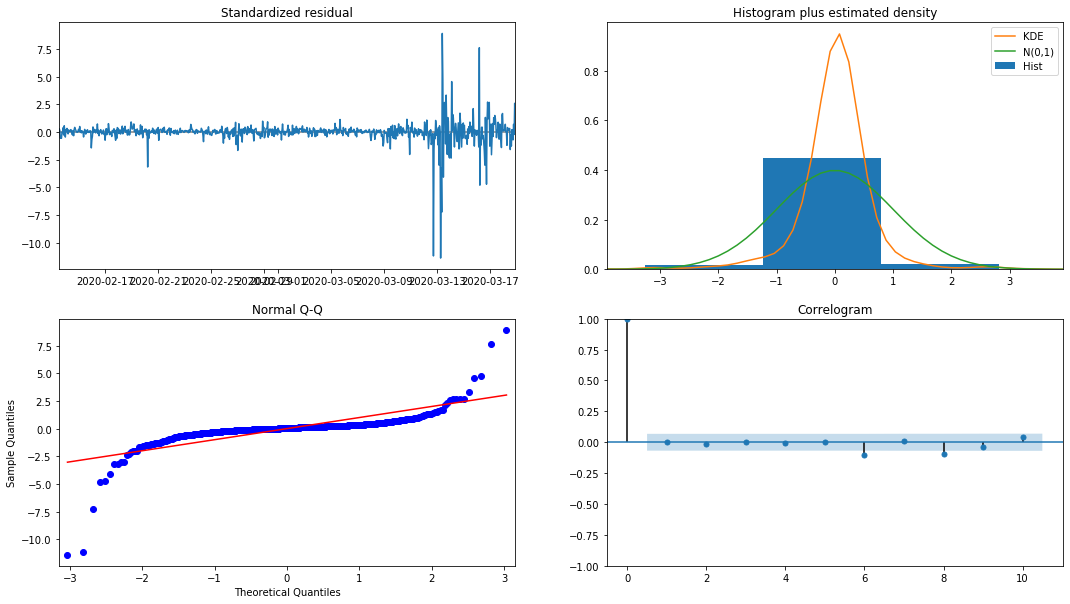
Mật độ xác suất KDE trong biểu đồ là xa so với phân bố bình thường N (0,1), cho thấy số dư không phải là một phân bố bình thường. Trong đồ thị lượng tử QQ, số dư của các mẫu lấy mẫu từ phân bố bình thường tiêu chuẩn không hoàn toàn theo xu hướng tuyến tính, vì vậy nó được xác nhận một lần nữa rằng số dư không phải là phân bố bình thường và gần với tiếng ồn trắng.

Sau đó, nói rằng, liệu mô hình có thể được sử dụng vẫn cần phải được thử nghiệm.

4-3. thử nghiệm mô hình

Hiệu ứng khớp của số dư không phải là lý tưởng, vì vậy chúng tôi đã thực hiện thử nghiệm Durbin Watson trên nó. Giả thuyết ban đầu của thử nghiệm là chuỗi không có tương quan tự động, và chuỗi giả thuyết thay thế là tĩnh. Ngoài ra, nếu giá trị P của các thử nghiệm LB, JB và H nhỏ hơn giá trị quan trọng của mức độ tin cậy 0,05%, giả thuyết ban đầu sẽ bị từ chối.

Trong [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

Ra khỏi [1]: Xét nghiệm heteroskedasticity của các dư lượng (breakvar): stat=24.598, p=0.000

Tính bình thường của xét nghiệm các dư lượng (jarquebera): stat=106398.739, p=0.000

Sự tương quan hàng loạt của các dư lượng thử nghiệm (ljungbox): stat=104.767, p=0.000

Xét nghiệm Durbin-Watson về dư lượng: d=2,00 (Lưu ý: 2 có nghĩa là không có mối tương quan hàng loạt, 0 = pos, 4 = âm)

Kiểm tra tất cả các gốc AR bên ngoài vòng tròn đơn vị (>1): Đúng

Xét nghiệm cho tất cả các gốc MA bên ngoài vòng tròn đơn vị (>1): Đúng

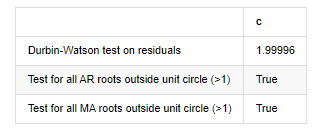
Trong [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

Ra khỏi [1]:

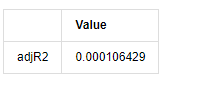
Nếu số liệu thống kê thử nghiệm Durbin Watson bằng 2, xác nhận rằng chuỗi không có mối tương quan, và giá trị thống kê của nó được phân phối giữa (0,4). Gần 0 có nghĩa là mối tương quan tích cực cao, trong khi gần 4 có nghĩa là mối tương quan tiêu cực cao. Ở đây nó gần bằng 2. Giá trị P của các thử nghiệm khác đủ nhỏ, gốc đặc trưng đơn vị nằm ngoài vòng tròn đơn vị, và càng lớn giá trị của adjR2 được sửa đổi, thì càng tốt. Kết quả tổng thể của phép đo dường như không thỏa mãn.

Trong [14]:

model_results.params

Ra khỏi [1]: chặn -0.000817 ma.L1 -0.102102 sigma2 0.000275 dtype: float64

Tóm lại, tham số đặt thứ tự này về cơ bản có thể đáp ứng các yêu cầu của mô hình hóa chuỗi thời gian và mô hình hóa biến động tiếp theo, nhưng hiệu ứng khớp là như vậy.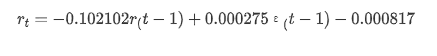

4-4. Dự đoán mô hình

Sau đó, mô hình được đào tạo được khớp với phía trước. statsmodels cung cấp các tùy chọn tĩnh và động cho việc khớp và dự báo. Sự khác biệt nằm ở việc liệu giá trị quan sát được sử dụng trong bước tiếp theo của dự báo, hoặc giá trị dự đoán được tạo trong bước trước được sử dụng lặp đi lặp lại. Các hiệu ứng dự đoán của log_return (tỷ lệ trở lại theo logaritm) là như sau:

Trong [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Ra khỏi [1]:

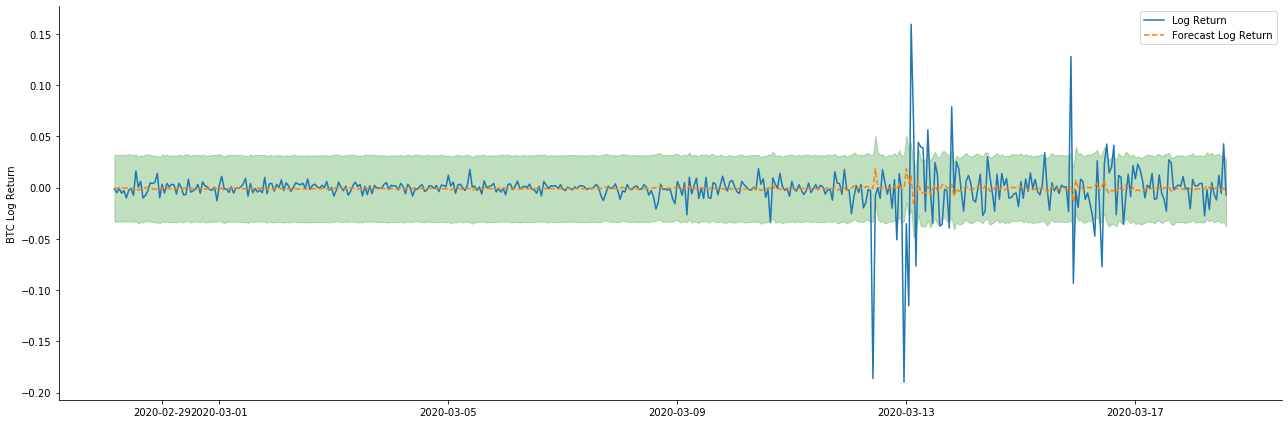
Có thể thấy rằng hiệu ứng phù hợp của chế độ tĩnh trên mẫu là tuyệt vời, dữ liệu mẫu có thể gần như được bao phủ bởi khoảng độ tin cậy 95%, và chế độ động hơi không kiểm soát được.

Vì vậy, hãy xem xét hiệu ứng khớp dữ liệu trong chế độ năng động:

Trong [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Ra khỏi [38]:

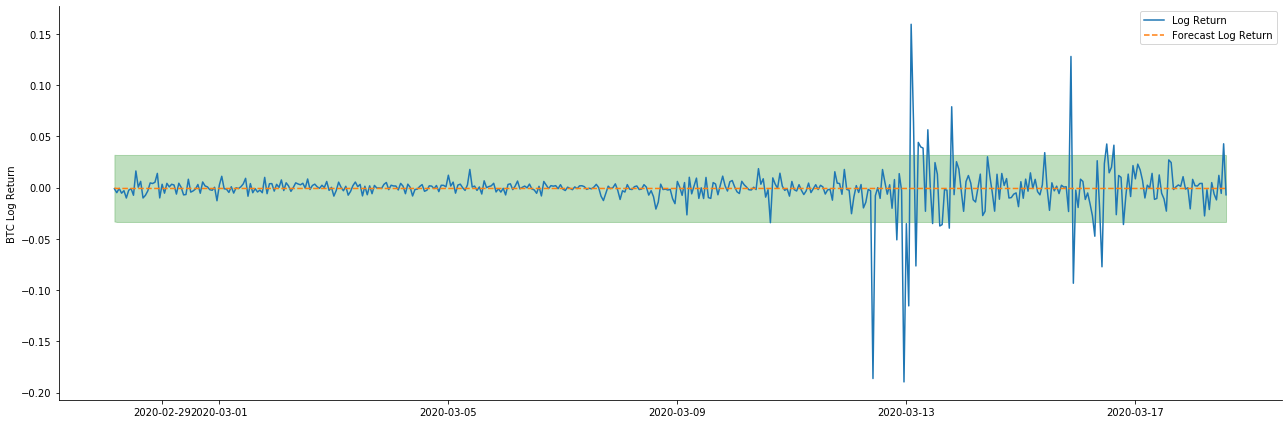
Có thể thấy rằng hiệu ứng phù hợp của hai mô hình trên mẫu là tuyệt vời, và giá trị trung bình có thể gần như được bao phủ bởi khoảng độ tin cậy 95%, nhưng mô hình tĩnh rõ ràng là phù hợp hơn.

Trong [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Ra khỏi [41]:

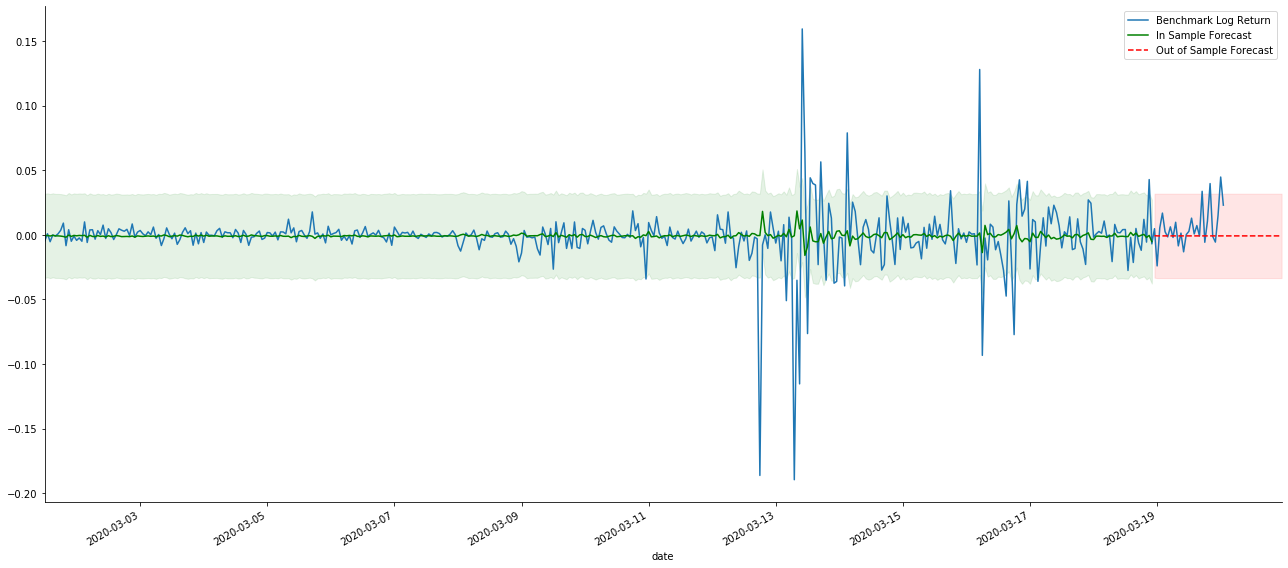
Bởi vì việc khớp dữ liệu trong mẫu là một dự đoán chuyển tiếp, khi lượng thông tin trong mẫu là đủ, mô hình tĩnh có xu hướng quá khớp, trong khi mô hình động thiếu biến phụ thuộc đáng tin cậy, và hiệu ứng trở nên tồi tệ hơn sau khi lặp lại. Khi dự đoán dữ liệu bên ngoài mẫu, mô hình tương đương với mô hình động trong mẫu, vì vậy độ chính xác của phạm vi lỗi của dự đoán dài hạn chắc chắn sẽ thấp.

Nếu chúng ta đảo ngược dự báo tỷ lệ lợi nhuận để log_price (giá logaritm), sự khớp được hiển thị trong hình dưới đây:

Trong [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Ra khỏi[42]:

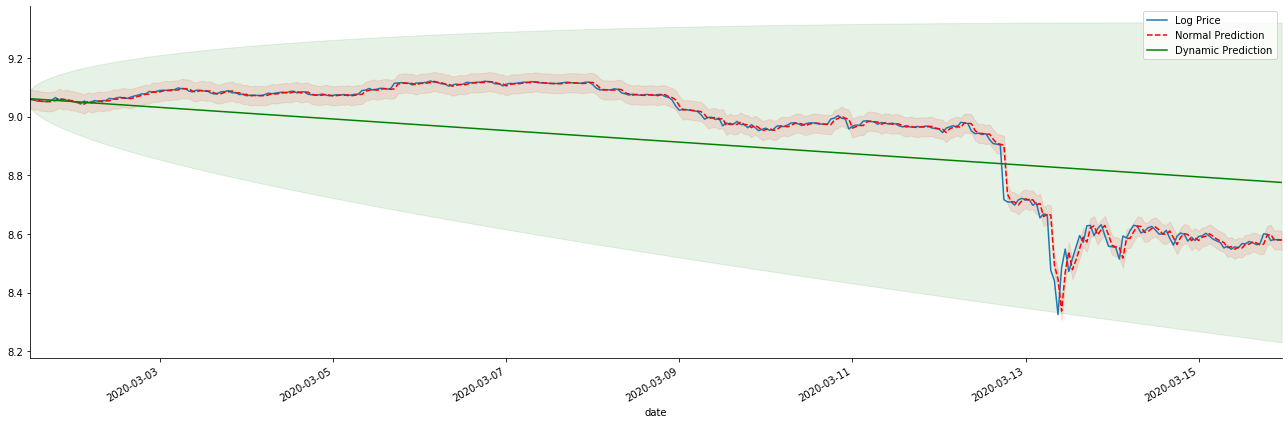
Bạn có thể thấy những lợi thế tương ứng của mô hình tĩnh và sự khác biệt cực lớn giữa mô hình động và mô hình tĩnh trong dự đoán dài hạn. Đường chấm màu đỏ và phạm vi màu hồng... Bạn không thể nói rằng dự đoán của mô hình này là sai. Sau tất cả, nó bao gồm xu hướng của đường trung bình động hoàn toàn, nhưng... nó có ý nghĩa không?

Trong thực tế, mô hình ARMA không sai, bởi vì vấn đề không phải là mô hình, mà là logic khách quan của các thứ. Mô hình chuỗi thời gian chỉ có thể được thiết lập dựa trên mối tương quan giữa các quan sát trước và sau đó. Do đó, không thể mô hình hóa chuỗi tiếng ồn trắng. Do đó, tất cả các công việc trước đây đều dựa trên giả định táo bạo rằng chuỗi tỷ lệ lợi nhuận của BTC không thể độc lập và phân phối giống hệt nhau.

Nói chung, các chuỗi tỷ lệ lợi nhuận là chuỗi chênh lệch martingale, có nghĩa là tỷ lệ lợi nhuận là không thể dự đoán, và giả định hiệu quả yếu của thị trường tương ứng được giữ. Chúng tôi đã giả định rằng tỷ lệ lợi nhuận trong các mẫu riêng lẻ có một mức độ tương quan tự động nhất định, và giả định phân phối tương tự cũng là để làm cho mô hình phù hợp áp dụng cho tập huấn, do đó mô hình ARMA đơn giản có thể được phù hợp, điều này chắc chắn sẽ có tác dụng dự đoán kém.

Tuy nhiên, chuỗi dư thừa khớp cũng là chuỗi chênh lệch martingale. chuỗi chênh lệch martingale có thể không độc lập và phân bố giống hệt nhau, nhưng biến thể có điều kiện có thể phụ thuộc vào giá trị trong quá khứ, do đó, sự tương quan tự tự thứ nhất đã biến mất, nhưng vẫn còn tương quan tự thứ cao hơn, đây cũng là điều kiện tiên quyết quan trọng để có thể mô hình hóa và quan sát biến động.

Nếu một logic như vậy đúng, thì tiền đề xây dựng các mô hình biến động khác nhau cũng đúng. Vì vậy, đối với một chuỗi tỷ lệ lợi nhuận, nếu một thị trường kém hiệu quả được thỏa mãn, thì giá trị trung bình phải khó dự đoán, nhưng sự khác biệt là có thể dự đoán. Và ARMA phù hợp cung cấp một chuẩn mực chuỗi thời gian chất lượng công bằng, sau đó chất lượng cũng xác định chất lượng dự đoán biến động.

Cuối cùng, hãy đánh giá hiệu quả của dự đoán một cách đơn giản.

Trong [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Ra khỏi [1]: Sai lầm hình vuông gốc trung bình (RMSE): 0,0184 Sai lầm hình vuông gốc trung bình (RMSE): 0,0167 Lỗi tỷ lệ tuyệt đối trung bình (MAPE): 2,25e+03 Lỗi tỷ lệ tuyệt đối trung bình (MAPE): 395

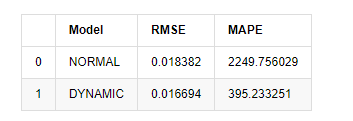
Có thể thấy rằng mô hình tĩnh tốt hơn một chút so với mô hình động về sự trùng hợp lỗi giữa giá trị dự đoán và giá trị thực tế. Nó phù hợp với tỷ lệ lợi nhuận logarithmic của Bitcoin tốt, về cơ bản phù hợp với mong đợi. Dự đoán động thiếu thông tin biến chính xác hơn, và lỗi cũng được phóng đại bởi lặp lại, do đó hiệu ứng dự đoán kém. MAPE lớn hơn 100%, vì vậy chất lượng phù hợp thực tế của cả hai mô hình không phải là lý tưởng.

Trong [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

Ra khỏi [1]:

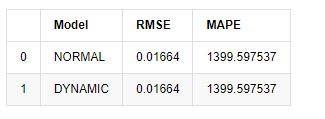
Vì dự đoán tiếp theo bên ngoài mẫu phụ thuộc vào kết quả của bước trước, chỉ có mô hình động là hiệu quả. Tuy nhiên, khi lỗi dài hạn của mô hình động dẫn đến khả năng dự đoán không đủ của mô hình tổng thể, vì vậy bước tiếp theo được dự đoán tối đa.

Tóm lại, mô hình tĩnh ARMA là mô hình phù hợp để khớp với tỷ lệ lợi nhuận trong mẫu của Bitcoin. Dự đoán ngắn hạn về tỷ lệ lợi nhuận có thể bao gồm khoảng thời gian tin cậy một cách hiệu quả, nhưng dự đoán dài hạn rất khó, đáp ứng hiệu quả yếu của thị trường. Sau khi thử nghiệm, tỷ lệ lợi nhuận trong khoảng thời gian mẫu đáp ứng tiền đề của quan sát biến động tiếp theo.

5. Hiệu ứng ARCH

Hiệu ứng mô hình ARCH là mối tương quan chuỗi của chuỗi heteroscedasticity có điều kiện. Thử nghiệm hỗn hợp Ljung Box được sử dụng để kiểm tra mối tương quan của chuỗi vuông dư để xác định liệu có hiệu ứng ARCH hay không. Nếu thử nghiệm hiệu ứng ARCH được vượt qua, tức là chuỗi có heteroscedasticity, bước tiếp theo của mô hình GARCH có thể được thực hiện để ước tính phương trình trung bình và phương trình biến động cùng nhau. Nếu không, mô hình cần được tối ưu hóa và điều chỉnh lại, chẳng hạn như xử lý khác biệt hoặc chuỗi tương đối.

Chúng tôi chuẩn bị một số bộ dữ liệu và biến thể toàn cầu ở đây:

Trong [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

Ra khỏi [33]:

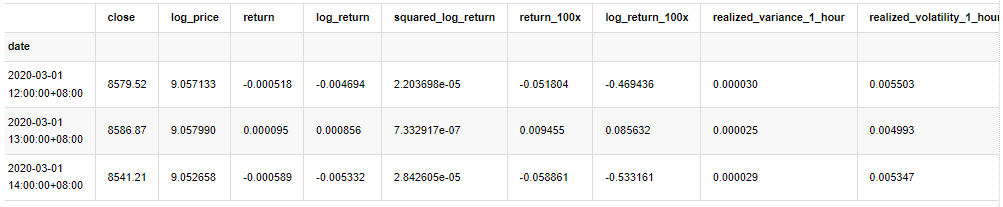
Trong [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Ra khỏi [1]:

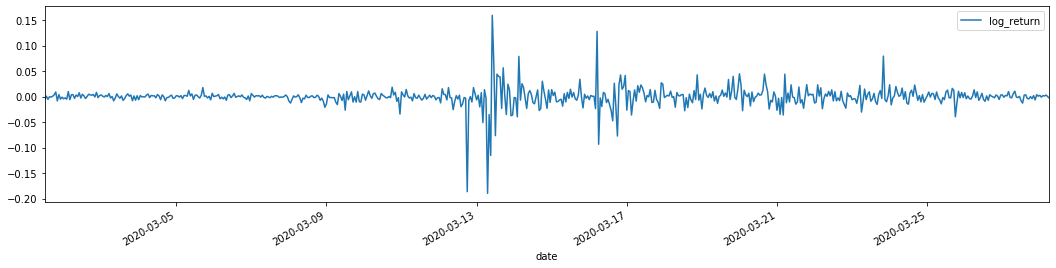
Các tỷ lệ trở lại logaritm được hiển thị ở trên. Tiếp theo, chúng ta cần kiểm tra hiệu ứng ARCH của mẫu. Chúng ta thiết lập chuỗi dư thừa trong mẫu dựa trên ARMA. Một số chuỗi và chuỗi vuông của dư thừa và dư thừa được tính toán đầu tiên:

Trong [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Ra khỏi [1]:

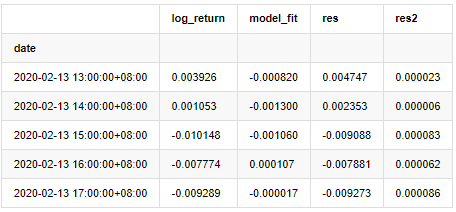
Sau đó, các chuỗi dư của mẫu được vẽ trên biểu đồ.

Trong [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Ra khỏi [1]:

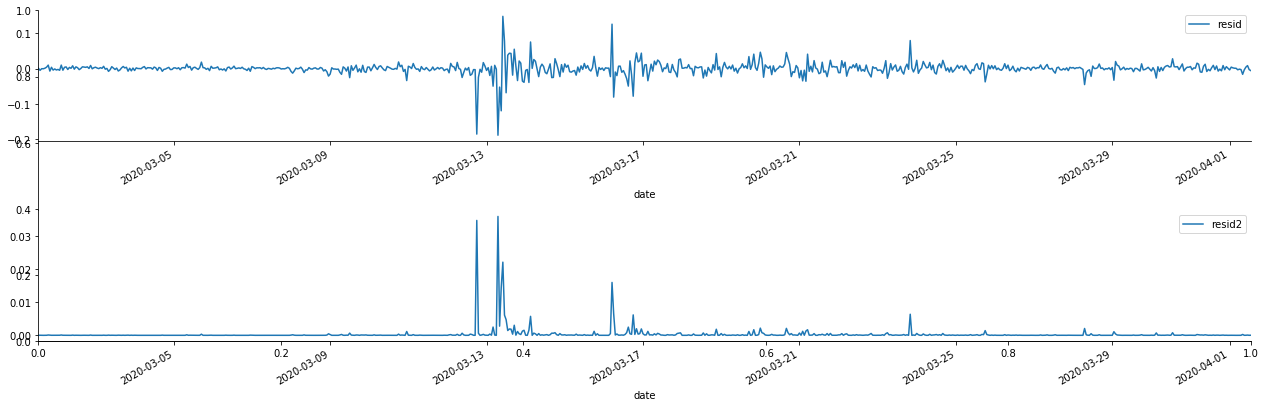
Có thể thấy rằng chuỗi dư có đặc điểm tổng hợp rõ ràng, và ban đầu có thể đánh giá rằng chuỗi có hiệu ứng ARCH.

Trong [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Ra ngoài[70]:

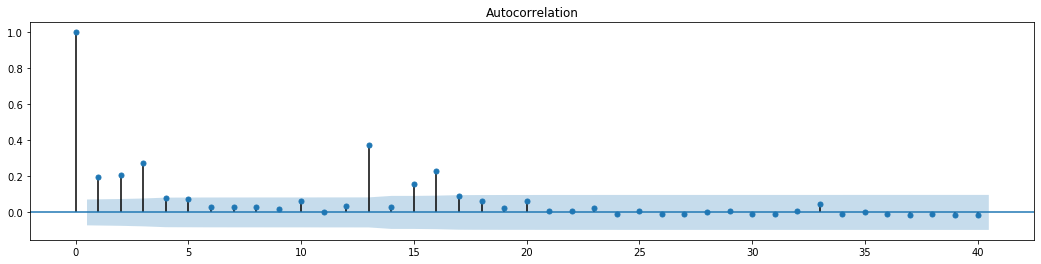
Giả định ban đầu cho thử nghiệm trộn chuỗi là chuỗi không có mối tương quan. Có thể thấy rằng các giá trị P tương ứng của 20 thứ tự dữ liệu đầu tiên thấp hơn giá trị quan trọng của mức độ tin cậy 0,05%. Do đó, giả định ban đầu bị từ chối, tức là phần còn lại của chuỗi có hiệu ứng ARCH. Mô hình biến thể có thể được thiết lập thông qua mô hình loại ARCH để phù hợp với tính heteroscedastic của chuỗi còn lại và dự đoán thêm sự biến động.

6. Mô hình hóa GARCH

Trước khi thực hiện mô hình GARCH, chúng ta cần phải giải quyết phần đuôi béo của chuỗi. Bởi vì thuật ngữ lỗi của chuỗi trong giả thuyết cần phải phù hợp với phân bố bình thường hoặc phân bố t, và chúng ta đã xác minh trước đó rằng chuỗi năng suất có phân bố đuôi béo, vì vậy chúng ta cần mô tả và bổ sung phần này.

Trong mô hình GARCH, mục lỗi cung cấp các tùy chọn phân bố bình thường, phân bố t, phân bố GED (Generalized Error Distribution) và phân bố t-Students skewed.

Có liên quan

Thêm nữa