风险小史(四) 棣莫弗与神之曲线

【风险小史】（四）棣莫弗与神之曲线

上一期说到，雅各布·伯努利在逝世的时候，还没有把自己关于概率论的书《猜度术》出版出来。整理他手稿的任务就交给了他的侄子尼古拉斯二世·伯努利（就是那个早夭的天才）。尼古拉斯在完成叔叔遗愿之后，又开始想要研究在已经确定了观察次数的情况下，对真实概率的偏差水平。可能天才冥冥中也觉得自己力不从心，于是就邀请棣莫弗加入到研究中来。 棣莫弗（Abraham de Moivre）在许多地方被翻译成棣美弗，不过看了他的画像后，我不是很赞成后面这种翻译法。本来这个邀请可以成就一段后世传颂的数（ji）学（you）界佳话，但是棣莫弗居然拒绝了。而且他拒绝的理由是，他觉得自己还没有足够的洪荒之力。

• 棣莫弗 棣莫弗其实只比雅各布·伯努利小十几岁，而他的整个人生实际上可以用一部小说来形容，那就是《悲惨世界》。那个时候法国是一个天主教氛围狂热的国家，而棣莫弗恰好或者恰不好是一个新教徒。后来法国国王路易十四又颁布了一条法令，宣布国内的新教徒是劣等公民，小朋友必须改信新教，这个套路基本上就在法国把新教定性成邪教了，而棣莫弗因此还坐了两年牢。出狱的棣莫弗设法跑到了英国，但是他始终没有在学术界获得教职，尽管他和牛顿是朋友，尽管他30岁就是英国皇家学会的会员。平时的棣莫弗靠给别人当数学家教和给赌徒当顾问维持生计，日常的基本构成是做数学、玩骰子和骂法国，结果带着这样的负能量他一直活到87岁，去世的时候，用比较委婉的说法形容是，又穷又瞎。

  不过我们还是要在这里大声呼吁，棣莫弗永垂不朽！1711年棣莫弗出版了一本《关于运气的测量》，如果那个时候出书有腰封的话，腰封上一定会写牛顿的推荐语：“去问棣莫弗先生，他在这方面懂的比我多。”

  

  可惜那个时候没有，所以棣莫弗也没法抱大腿赚到太多版税。

  你应该还记得我们在前一篇的那个问题（风险小史（三）：少壮伯努利），对于罐子里的5000个鹅卵石，我们可以进行25500次抓取来估计总体鹅卵石的比例。但是你应该也能发现，25500次重复抓取实在太多了，还不如把石头倒出来一个一个数。棣莫弗对个问题想到了一个非常好的解决办法，不谦虚地说，这个方法思路之清奇，彪炳数学史。

  利用微积分和帕斯卡三角的方法，棣莫弗采取了分组抽样的方法。他假定，每次都从罐子里抓100个鹅卵石出来，记下黑白色鹅卵石的比例后把石头又放回去，然后再进行同样的抽取。通过这样的方法，棣莫弗可以事先告诉你你记录的比例与真实比例的近似偏差，并且这些比率是如何分布在它们的平均值周围的。

  这个说法是不是似曾相识，是不是感觉就在嘴边，是不是马上就想呼喊它的名字？对，这个就是大家所熟悉的正态分布。正态分布的曲线像一条钟形曲线，大多数观察值聚集在中间，接近所有观察值的均值，然后从均值处对称地向两端倾斜，并且均值两端的观察值数目是相等的。在一开始曲线是快速向下倾斜的，而在两端，这样的倾斜会变得扁平，这意味着，距离均值越远的观察值出现的概率越小。很多年后，任意找一本统计学课本，都有对这条曲线的描述，并且称呼它为棣莫弗中心极限定理。

  

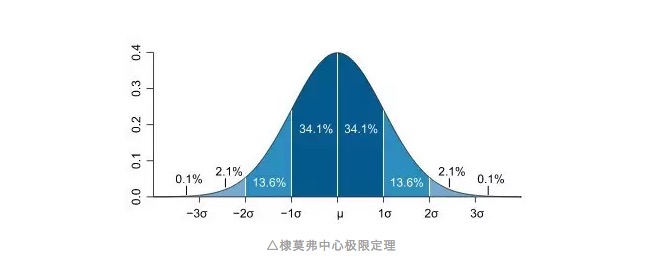
  这样我们就可以引入标准差的概念了，其实在公众号的其他文章中（为什么是标准差？大神眼中的风险测量）我们已经提到过它了。标准差其实形容了观察值对均值的偏离程度，或者我们把它理解成对均值偏离的单位。对于一个正态分布而言，我们抽取的100个一组的鹅卵石的比例值，大概会有68%落在均值两侧一个标准差的范围以内，而两个标准差的范围就大概可以囊括95%的观察值。

  作为一名虔诚的教徒，棣莫弗认为钟形曲线是神的产物。在他看来，通过这样的测量我们就可以战胜不确定性，进而征服所有的风险，因为曲线上已经描述了所有可能出现的现象及其概率，也许出于偶然会产生所谓的偏离，但是随着时间的推移，这些偏离不会再影响我们总结出的规律。

  用大家喜闻乐见的方式解释棣莫弗的话，就是“失望是偶尔拨不通的电话号码，多试几次，总会回答”。中学还有一个经典的题目（咦，为什么我老是用中学的题目）是关于产品合格率的。假如对于一批产品，行业标准认为废品率不超过0.1%就是合格，这意味着我们随便从产品里选取10000个，其中如果废品不超过10个，就合格了。但是结果在这10000个里最后出现了12个，如果平均而言产品的废品率都是0.1%，其实我们可以利用棣莫弗的方法，计算出现12个废品的概率是多少。

  不过这个问题在大多数时候，对于我们是没啥意义的。因为其实我们可能并不知道产品平均的废品率会是多少，如果平均废品率高于检测标准，那么我们一批产品通过检验的可能性会有多大？如果抽取20000个产品做检测，那10000个产品的结果可以拿过来直接用吗？这些问题好像用棣莫弗的曲线来解释就太麻烦了。于是，一个叫贝叶斯的、会出现在所有统计学和博弈论教材里的名字，就此出现了，而这也会是我们下一期的内容。

转载自 中国量化投资学会