এই নিবন্ধে, আমরা Ornstein-Uhlenbeck প্রক্রিয়ার একটি সংক্ষিপ্ত বিবরণ দেব, এর গাণিতিক সূত্র বর্ণনা করব, পাইথন ব্যবহার করে এটি বাস্তবায়ন ও মডেল করব এবং কোয়ান্টাম ফিনান্স এবং সিস্টেম ট্রেডিংয়ের কিছু বাস্তব প্রয়োগ নিয়ে আলোচনা করব। আমরা একটি আরও উন্নত র্যান্ডম প্রক্রিয়া মডেল ব্যবহার করব, যাকে Ornstein-Uhlenbeck (OU) প্রক্রিয়া বলা হয়, যা সমতুল্য রিটার্ন আচরণ প্রদর্শন করে এমন একটি রিটার্ন টাইম সিকোয়েন্স মডেলিংয়ের জন্য ব্যবহার করা যেতে পারে। এটি বিশেষত ডেরাইভেটিভের মূল্য নির্ধারণের মধ্যে সুদের হার মডেলিং এবং ব্যবসায়ের সময় সিস্টেম ট্রেডিংয়ের জন্য অ্যালগরিদমিকভাবে কাজ করার জন্য দরকারী।

Ornstein-Uhlenbeck প্রক্রিয়া কি?

অর্নস্টাইন-উহেলেনবেক প্রক্রিয়া হল একটি ধারাবাহিক সময়-র্যান্ডম প্রক্রিয়া যা গড়-মূল্য রিগ্রেশন কার্যকলাপের মডেলিংয়ের জন্য ব্যবহৃত হয়। এর মানে হল যে, স্ট্যান্ডার্ড র্যান্ডম ড্রিফট বা ব্রাউন মুভমেন্টের বিপরীতে, যা অসীমভাবে ড্রিফট করতে পারে, OU প্রক্রিয়াটি প্রায়শই সময়ের সাথে সাথে দীর্ঘমেয়াদী গড়ের দিকে ফিরে আসে। গাণিতিকভাবে বলতে গেলে, OU প্রক্রিয়াটি এই গড়-মূল্য রিগ্রেশন কার্যকলাপকে নিয়ন্ত্রণ করার জন্য নির্দিষ্ট র্যান্ডম ডিফারেনশিয়াল সমীকরণ (এসডিই) এর সমাধান। OU প্রক্রিয়াটির এসডিই নিম্নলিখিত সূত্র দ্বারা দেওয়া হয়ঃ

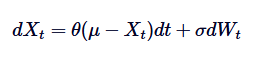
এর মধ্যে, Xt হল সময় t তে একটি এলোমেলো প্রক্রিয়া, μ হল দীর্ঘমেয়াদী গড়, θ হল গড় রিটার্ন হার, δ হল ভোল্টেবিলিটি, এবং dWt হল উইনার প্রক্রিয়া বা স্ট্যান্ডার্ড ব্রাউন আন্দোলন।

ঐতিহাসিক পটভূমি ও প্রয়োগ

অর্নস্টাইন-উহেলেনবেক প্রক্রিয়াটি প্রথম ১৯৩০ সালে লিওনার্ড অর্নস্টাইন এবং জর্জ ইউজিন উহেলেনবেক দ্বারা উদ্ভাবিত হয়েছিল, ঘর্ষণের শর্তে ব্রাউন গতির কণার গতির অনুকরণ করার জন্য। সময়ের সাথে সাথে, এর ব্যবহারিকতা পদার্থবিজ্ঞানের বাইরে চলে গেছে এবং জীববিজ্ঞান, রসায়ন, অর্থনীতি এবং অর্থনীতির মতো বিভিন্ন ক্ষেত্রে প্রয়োগ করা হয়েছে।

কোয়ান্টাম ফাইন্যান্সে, OU প্রক্রিয়াটি গড় মানের রিটার্নের আচরণ প্রদর্শন করে এমন ঘটনাকে মডেলিংয়ের জন্য বিশেষভাবে উপযোগী। উল্লেখযোগ্য উদাহরণগুলির মধ্যে রয়েছে সুদের হার, বিনিময় হার এবং আর্থিক বাজারের অস্থিরতা। উদাহরণস্বরূপ, জনপ্রিয় সুদের হার মডেল ভ্যাসিকেক মডেলটি সরাসরি OU প্রক্রিয়া থেকে প্রাপ্ত।

কোয়ান্টাম ফিনান্সিং এর গুরুত্ব

অর্নস্টাইন-উহেলেনবেক প্রক্রিয়াটি কোয়ান্টাম ফিনান্সে গুরুত্বপূর্ণ কারণগুলি হলঃ এর গড় রিটার্নাল প্রকৃতি এটিকে আর্থিক পরিবর্তনশীলগুলির মডেলিংয়ের জন্য একটি প্রাকৃতিক পছন্দ করে তোলে, যা এলোমেলোভাবে চলাচল করে না, বরং স্থিতিশীলতার চারপাশে দীর্ঘমেয়াদী গড় মানের ওঠানামা করে। এই বৈশিষ্ট্যটি সুদের হার মডেলিংয়ের জন্য গুরুত্বপূর্ণ, যেখানে গড় রিটার্নাল কেন্দ্রীয় ব্যাংকের দীর্ঘমেয়াদী স্থিতিশীল সুদের হারের প্রভাবকে প্রতিফলিত করে।

উপরন্তু, OU প্রক্রিয়াটি সম্পদ মূল্যের মডেলিংয়ের জন্য ব্যবহৃত হয় (উত্পাদিত মূল্য সহ) এবং ঝুঁকি ব্যবস্থাপনা কৌশল। এটি আরও জটিল মডেলের বিল্ডিং ব্লক হিসাবেও কাজ করতে পারে, যেমন কক্স-ইঙ্গারসোল-রস (সিআইআর) মডেল, যা OU প্রক্রিয়াটিকে একটি অ-নেতিবাচক মানযুক্ত সুদের হার মডেলিংয়ের জন্য প্রসারিত করে।

প্রধান বৈশিষ্ট্য এবং অন্তর্দৃষ্টি

Ornstein-Uhlenbeck প্রক্রিয়ার প্রধান বৈশিষ্ট্যগুলি নিম্নরূপ সংক্ষিপ্ত করা যায়ঃ

• গড় রিটার্নঃOU প্রক্রিয়াটি দীর্ঘমেয়াদী গড়ের দিকে ফিরে যায়। এটি ব্রাউন আন্দোলন এবং অন্যান্য প্রক্রিয়াগুলির সাথে বিপরীত, যা এই প্রবণতা প্রদর্শন করে না।
• অস্থিরতা:প্যারামিটার δ নিয়ন্ত্রণ প্রক্রিয়ার মধ্যে এলোমেলোতা বা অস্থিরতার মাত্রা। অস্থিরতা যত বেশি, প্রক্রিয়াটি প্রত্যাবর্তনের আগে গড় থেকে তত বেশি বিচ্যুত হয়।
• প্রত্যাবর্তন গতিঃথেরাপিটি নির্ধারণ করে যে প্রক্রিয়াটি কত দ্রুত গড়ের দিকে ফিরে আসে। থেরাপিটি যত বেশি, তত দ্রুত গড়ের দিকে ফিরে আসে।
• স্থিতিশীলতা:OU প্রক্রিয়াটি স্থিতিশীল, যার অর্থ হল এর পরিসংখ্যানগত বৈশিষ্ট্যগুলি সময়ের সাথে পরিবর্তিত হয় না। এটি আর্থিক ক্ষেত্রে স্থিতিশীল সিস্টেমের মডেলিংয়ের জন্য গুরুত্বপূর্ণ।

স্বজ্ঞাতভাবে বলতে গেলে, আপনি অর্নস্টাইন-উহেলেনবেক প্রক্রিয়াটিকে গড়ের চারপাশে প্রসারিত কার্সারির আচরণকে মডেলিং হিসাবে বিবেচনা করতে পারেন। যদিও প্রক্রিয়াটি এলোমেলোভাবে ওঠানামা করে গড় থেকে বিচ্যুত হতে পারে, কার্সারির টান প্যানেলটি ((গড়ের প্রত্যাবর্তনের মতো) নিশ্চিত করে যে এটি শেষ পর্যন্ত গড়ের দিকে ফিরে আসে।

অন্যান্য এলোমেলো প্রক্রিয়াগুলির সাথে তুলনা

যেহেতু OU প্রক্রিয়াটি বিভিন্ন আর্থিক ঘটনার মডেলিংয়ের সাথে ঘনিষ্ঠভাবে সম্পর্কিত, তাই এটি প্রায়শই অন্যান্য এলোমেলো প্রক্রিয়াগুলির সাথে তুলনা করা হয় (যেমন ব্রাউন মুভমেন্ট এবং জ্যামিতিক ব্রাউন মুভমেন্ট (GBM)) । ব্রাউন মুভমেন্টের বিপরীতে (ব্রাউন মুভমেন্টের কোন প্রত্যাবর্তন গড় মানের প্রবণতা নেই), OU প্রক্রিয়াটির একটি সুস্পষ্ট গড় মানের প্রত্যাবর্তন আচরণ রয়েছে। এটি স্থিতিশীল ভারসাম্যপূর্ণ তরঙ্গের চারপাশে ভেরিয়েবলের দৃশ্যের মডেলিংয়ের জন্য আরও উপযুক্ত করে তোলে।

GBM-এর তুলনায়, যা সাধারণত শেয়ারের দামের মডেলিংয়ের জন্য ব্যবহৃত হয় এবং এতে ড্রিফট এবং ওভারল্যাপিংয়ের উপাদান থাকে, OU প্রক্রিয়াটি সূচকীয় বৃদ্ধি প্রদর্শন করে না, বরং তার গড়ের চারপাশে ওভারল্যাপিং করে। GBM সময়ের সাথে সাথে বাড়তে থাকা পরিমাণের মডেলিংয়ের জন্য আরও উপযুক্ত, যখন OU প্রক্রিয়াটি পরিবর্তিতদের মডেলিংয়ের জন্য উপযুক্ত যা গড়ের রিটার্ন বৈশিষ্ট্য প্রদর্শন করে।

কোয়ান্টাম ফাইন্যান্সের উদাহরণ

অর্নস্টাইন-উহেলেনবেক প্রক্রিয়াটি আর্থিক ক্ষেত্রে ব্যাপকভাবে প্রয়োগ করা হয়, বিশেষত মডেলিং পরিস্থিতিতে যেখানে গড় মানের প্রত্যাবর্তন একটি গুরুত্বপূর্ণ বৈশিষ্ট্য। নীচে আমরা কয়েকটি সাধারণ ব্যবহারের ক্ষেত্রে আলোচনা করব।

সুদের মডেলিং

OU প্রক্রিয়ার অন্যতম উল্লেখযোগ্য প্রয়োগ হ’ল সুদের হারকে মডেলিং করা, বিশেষত ভ্যাসিকেক মডেলের কাঠামোর মধ্যে। ভ্যাসিকেক মডেল অনুমান করে যে সুদের হারগুলি OU প্রক্রিয়া অনুসরণ করে, অর্থাৎ সুদের হারগুলি সময়ের সাথে সাথে দীর্ঘমেয়াদী গড়ের দিকে ফিরে আসে। এই বৈশিষ্ট্যটি সুদের হারের আচরণের সঠিকভাবে মডেল করার জন্য গুরুত্বপূর্ণ, কারণ সুদের হারগুলি অনির্দিষ্টকালের জন্য ওঠানামা করে না, বরং অর্থনৈতিক অবস্থার দ্বারা প্রভাবিত গড়ের কাছাকাছি ওঠানামা করে।

সম্পদ মূল্য নির্ধারণ

সম্পদ মূল্যায়নে, বিশেষত ফিক্সড রিটার্ন সিকিউরিটিজগুলিতে, OU প্রক্রিয়াটি সাধারণত বন্ডের রিটার্নের বিবর্তনকে অনুকরণ করার জন্য ব্যবহৃত হয়। OU প্রক্রিয়াটির গড় মূল্যের পুনরাবৃত্তিমূলক প্রকৃতি নিশ্চিত করে যে রিটার্নগুলি তাদের historicalতিহাসিক গড় থেকে খুব বেশি দূরে সরে যায় না, যা পর্যবেক্ষণ করা বাজার আচরণের সাথে সামঞ্জস্যপূর্ণ। এটি OU প্রক্রিয়াটিকে বন্ড এবং অন্যান্য সুদের সংবেদনশীল যন্ত্রের মূল্য নির্ধারণের জন্য একটি মূল্যবান হাতিয়ার করে তোলে।

জোড়া ট্রেডিং কৌশল

পেয়ারিং ট্রেডিং একটি বাজার-নিরপেক্ষ কৌশল যা দুটি সম্পর্কিত সম্পদের মধ্যে একটি ওভারওয়েট অবস্থান স্থাপন করে। এই ক্ষেত্রে, OU প্রক্রিয়াটি বিশেষভাবে কার্যকর কারণ এটি দুটি সম্পদের মধ্যে মূল্যের পার্থক্যকে মডেল করতে পারে, এবং মূল্য সাধারণত গড়ের রিটার্ন হয়। OU প্রক্রিয়াটি ব্যবহার করে মূল্যের পার্থক্যকে মডেলিং করে, ব্যবসায়ীরা যখন দামগুলি তাদের গড় থেকে বিচ্যুত হয় তখন লাভজনক প্রবেশ এবং প্রস্থান পয়েন্টগুলি নিশ্চিত করতে পারে, গড়ের রিটার্নের পূর্বাভাস দিতে পারে এবং এইভাবে একটি ট্রেডিং সংকেত তৈরি করতে পারে।

উদাহরণস্বরূপ, যদি দুটি ফরচার্ডের মধ্যে মূল্যের পার্থক্য একটি নির্দিষ্ট অবমূল্যায়ন অতিক্রম করে, তবে ব্যবসায়ীরা দুর্দান্ত পারফরম্যান্সের ফরচার্ডটি কভার করতে পারে এবং দুর্বল পারফরম্যান্সের ফরচার্ডটি আরও বেশি করতে পারে, আশা করে যে মূল্যের পার্থক্যটি তার historicalতিহাসিক গড় স্তরে ফিরে আসবে, যার ফলে বিপরীত হওয়ার সময় লাভ হবে।

Ornstein-Uhlenbeck SDE এর সমাধান

Ornstein-Uhlenbeck প্রক্রিয়াটির বিভাজক সমীকরণ সূত্রটি এর সমাধানের ভিত্তি। এই SDE সমাধানের জন্য, আমরা বিভাজক গুণক ব্যবহার করেছি। এসডিই পুনরায় লিখুনঃ

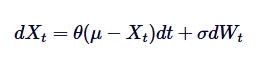
প্রথমত, আমরা উভয় পক্ষকে 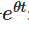দ্বারা গুণ করবঃ

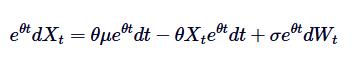
মনে রাখবেন, যদি আমরা উভয় পাশে 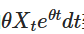যোগ করি, তাহলে বামদিকে বিভাজনকে গুণিতক হিসাবে প্রকাশ করা যেতে পারেঃ

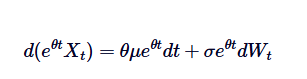
আমরা 0 থেকে t পর্যন্ত উভয় পক্ষকে পূর্ণসংখ্যা করি, এবং আমরা পাই:

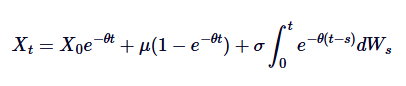
এটি Ornstein-Uhlenbeck SDE এর সাধারণ ব্যাখ্যা।

উপরের উপস্থাপিত সুস্পষ্ট সমাধানের বেশ কয়েকটি গুরুত্বপূর্ণ অর্থ রয়েছে। প্রথমটি 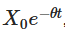যা দেখায় যে প্রাথমিক মানটি সময়ের সাথে সাথে হ্রাস পায় এবং কীভাবে প্রক্রিয়াটি ধীরে ধীরে তার সূচনাকে ভুলে যায়। দ্বিতীয়টি 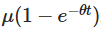যা দেখায় যে প্রক্রিয়াটি সময়ের সাথে সাথে গড়ের দিকে অগ্রসর হয়।

এই সমাধানটি নিশ্চিত গড় মানের রিটার্নের আচরণ এবং ব্রাউন গতি দ্বারা চালিত র্যান্ডম স্কোরের মধ্যে ভারসাম্যকে জোর দেয়। এই সমাধানটি বোঝা OU প্রক্রিয়াটি কার্যকরভাবে অনুকরণ করার জন্য গুরুত্বপূর্ণ, যেমনটি নীচে বর্ণিত হয়েছে।

অন্যান্য এলোমেলো প্রক্রিয়ার সাথে সংযোগ

Ornstein-Uhlenbeck প্রক্রিয়ার অন্যান্য বিখ্যাত এলোমেলো প্রক্রিয়ার সাথে বেশ কিছু গুরুত্বপূর্ণ সংযোগ রয়েছে (যেমন ব্রাউন আন্দোলন এবং ভ্যাসিকেক মডেল) ।

ব্রাউন আন্দোলনের সাথে সম্পর্ক

Ornstein-Uhlenbeck প্রক্রিয়াকে ব্রাউন মুভমেন্টের গড়-মূল্য রিটার্ন সংস্করণ হিসেবে দেখা যেতে পারে। ব্রাউন মুভমেন্ট এমন একটি প্রক্রিয়াকে বর্ণনা করে যার স্বাধীন বৃদ্ধি রয়েছে এবং যার গড়-মূল্য রিটার্ন নেই, এবং OU প্রক্রিয়াটি ব্রাউন মুভমেন্টকে ড্রিফট কমান্ড ব্যবহার করে গড়-মূল্য রিটার্ন প্রবর্তন করে, যার ফলে প্রক্রিয়াটি কেন্দ্রীয় মানের দিকে টানা হয়। গাণিতিকভাবে, যদি আমরা θ = 0 সেট করি, তাহলে OU প্রক্রিয়াটি স্ট্যান্ডার্ড ব্রাউন মুভমেন্টের সাথে সংক্ষিপ্ত করা হবে, যার সাথে ওভারলিং রয়েছেঃ

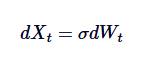
সুতরাং, ব্রাউন আন্দোলন হল OU প্রক্রিয়ার একটি বিশেষ দৃষ্টান্ত, যা গড় মানের রিটার্নের অনুপস্থিতির সাথে সম্পর্কিত।

ভাসিকের মডেলের সাথে সম্পর্ক

Vasicek মডেলটি সুদের হার মডেলিংয়ের জন্য ব্যাপকভাবে ব্যবহৃত হয়, যা মূলত সুদের হারের বিবর্তনে Ornstein-Uhlenbeck প্রক্রিয়ার একটি প্রয়োগ। Vasicek মডেলটি সুদের হারকে OU প্রক্রিয়ার অনুসরণ করে বলে মনে করে, যেখানে SDE সংজ্ঞায়িত করা হয়েছেঃ

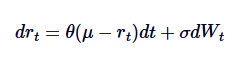
এর মধ্যে, rt স্বল্পমেয়াদী সুদের হারকে নির্দেশ করে, যার ব্যাখ্যা, θ, μ এবংδ এর সাথে OU প্রক্রিয়ার ব্যাখ্যা অনুরূপ। ভ্যাসিকেক মডেলটি সুদের হারের গড় মান পুনরুদ্ধারের পথ তৈরি করতে সক্ষম, যা আর্থিক মডেলিংয়ে এর প্রধান সুবিধাগুলির একটি।

এই সম্পর্কগুলো বোঝার ফলে আরও বিস্তৃতভাবে বোঝা যায় যে OU প্রক্রিয়াটি বিভিন্ন পরিবেশে কীভাবে ব্যবহৃত হয়, বিশেষত আর্থিক ক্ষেত্রে। আমরা নীচে উদাহরণে ব্যবহারের ক্ষেত্রে এই সংযোগগুলির ব্যবহারিক অর্থ নিয়ে আলোচনা করব।

Python ব্যবহার করে Ornstein-Uhlenbeck প্রক্রিয়ার অনুকরণ

এই বিভাগে, আমরা আলোচনা করব কিভাবে পাইথন ব্যবহার করে Ornstein-Uhlenbeck ((OU) প্রক্রিয়া মডেল করা যায়। এটি OU প্রক্রিয়া সংজ্ঞায়িত করার জন্য Euler-Maruyama বিচ্ছিন্নকরণ ব্যবহার করে বিচ্ছিন্নকরণের জন্য র্যান্ডম মাইক্রোডফারেনশিয়াল সমীকরণ (SDE) ।

এসডিইর বিচ্ছিন্নতা

এসডিই (SDE) -এর গাণিতিক সূত্রের উপর একটি নজর দেওয়া যাক এবং প্রতিটি শব্দকে সংক্ষিপ্তভাবে বর্ণনা করা যাকঃ

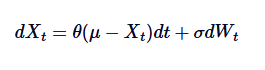
মধ্যে

• Xt হল প্রক্রিয়াটির মান সময় t তে।
• θ হল গড় মান প্রত্যাবর্তনের গতি।
• μ হল প্রক্রিয়াটির দীর্ঘমেয়াদী গড়।
• δ হল ভোল্টেবল হার প্যারামিটার।
• dWt হল Wiener প্রক্রিয়ার বৃদ্ধি (স্ট্যান্ডার্ড ব্রাউন আন্দোলন) ।

কম্পিউটারে এই প্রক্রিয়াটি অনুকরণ করার জন্য, আমাদের ধারাবাহিক সময় SDE এর বিচ্ছিন্নকরণ প্রয়োজন। একটি সাধারণ পদ্ধতি হল Euler-Maruyama বিচ্ছিন্নকরণ, যা ছোট বিচ্ছিন্ন সময় ধাপ / upload/asset/28db85708af6d062dda8d.png বিবেচনা করে ধারাবাহিক প্রক্রিয়াটির কাছাকাছি আসে। অর্নস্টাইন-উহেনবেক প্রক্রিয়াটির বিচ্ছিন্ন রূপটি নিম্নলিখিত ফর্ম দ্বারা দেওয়া হয়েছেঃ

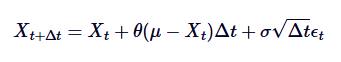
এর মধ্যে, 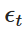হল স্ট্যান্ডার্ড অ্যানালগ ডিস্ট্রিবিউশন থেকে নিষ্কাশিত একটি র্যান্ডম ভেরিয়েবল (অর্থাৎ 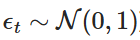) । এই বিচ্ছিন্নতা আমাদেরকে সময়ের সাথে সাথে Xt এর মানকে পুনরাবৃত্তভাবে গণনা করতে সক্ষম করে, যার ফলে OU প্রক্রিয়াটির আচরণ অনুকরণ করা যায়।

পাইথন বাস্তবায়ন

এখন আসুন আমরা পাইথন ব্যবহার করে Ornstein-Uhlenbeck প্রক্রিয়ার বিচ্ছিন্নতা বাস্তবায়ন করি। আমরা কেবল NumPy এবং Matplotlib পাইথন লাইব্রেরি ব্যবহার করি।

প্রথমে, আমরা NumPy এবং Matplotlib-কে স্ট্যান্ডার্ড পদ্ধতিতে আমদানি করি। তারপর, আমরা OU মডেলের জন্য সমস্ত প্যারামিটার নির্দিষ্ট করি। এরপর, আমরা একটি NumPy অ্যারে N-এর দৈর্ঘ্য দিয়ে বরাদ্দ করি, যাতে OU পাথ গণনা করার পরে এটি যুক্ত করা যায়। তারপর আমরা N-1 ধাপটি পুনরাবৃত্তি করি (ধাপ 1 হল নির্দিষ্ট প্রাথমিক শর্ত X0), dW এর র্যান্ডম ইনক্রিমেন্টের অনুকরণ করি, তারপর উপরের গাণিতিক সূত্রের ভিত্তিতে OU পাথের পরবর্তী পুনরাবৃত্তি গণনা করি। অবশেষে, Matplotlib ব্যবহার করে পাথের ইতিহাস আঁকুন।

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

ছবির ফলাফল নিম্নরূপঃ

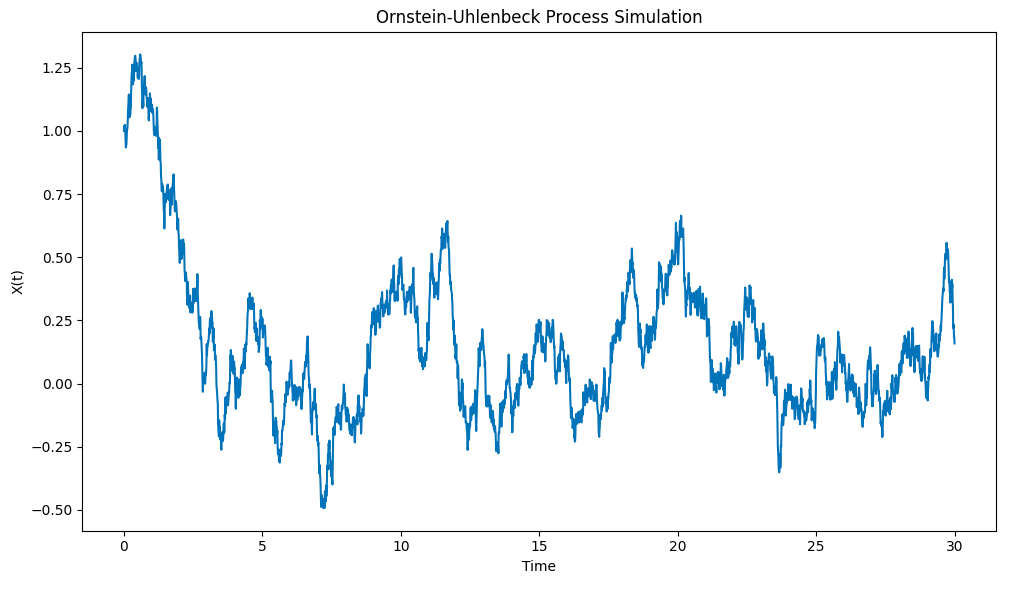
পাইথন দিয়ে অঙ্কিত অর্নস্টাইন-উহেলেনবেক প্রক্রিয়া সিমুলেশন

লক্ষ্য করুন কিভাবে এই প্রক্রিয়াটি প্রাথমিক শর্ত থেকে দ্রুত X0 = 1 থেকে গড় মান μ = 0 পর্যন্ত টানতে পারে এবং তারপর যখন এটি সেই গড় মান থেকে বিচ্যুত হয়, তখন এটি সেই গড় মানের দিকে ফিরে যাওয়ার প্রবণতা দেখায়।

সারসংক্ষেপ এবং পরবর্তী পদক্ষেপ

এই নিবন্ধে, আমরা Ornstein-Uhlenbeck প্রক্রিয়াটির একটি সংক্ষিপ্ত বিবরণ দিয়েছি, এর গাণিতিক সূত্রগুলি বর্ণনা করেছি এবং ধারাবাহিক সময় SDE এর একটি বিচ্ছিন্ন সংস্করণ অনুকরণ করার জন্য পাইথনের একটি মৌলিক বাস্তবায়ন সরবরাহ করেছি। পরবর্তী নিবন্ধে, আমরা OU প্রক্রিয়াটির উপর ভিত্তি করে নির্মিত আরও জটিল SDE গুলি নিয়ে কাজ করব এবং কীভাবে সেগুলি সিস্টেম ট্রেডিং এবং ডেরাইভেটিভ মূল্যের অ্যাপ্লিকেশনগুলিতে ব্যবহৃত হয় তা জানব।

সম্পূর্ণ কোড

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

মূল নিবন্ধের লিঙ্কঃ http://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/