এসপিওয়াই এবং আইডব্লিউএম-এর মধ্যে একটি ইনট্রা-ডে মিডিয়ান রিভার্সন জুটি কৌশল ব্যাকটেস্টিং
লেখক:ভাল, তৈরিঃ 2019-03-28 10:51:06, আপডেটঃএই নিবন্ধে আমরা আমাদের প্রথম ইনট্রাডে ট্রেডিং কৌশল বিবেচনা করতে যাচ্ছি। এটি একটি ক্লাসিক ট্রেডিং ধারণা,
কৌশলটি ব্যাপকভাবে ইটিএফ জোড়ার মধ্যে একটি
কৌশলটির যুক্তি হল যে এসপিওয়াই এবং আইডব্লিউএম প্রায় একই পরিস্থিতিকে চিহ্নিত করছে, যা বড় মূলধন এবং ছোট মূলধনযুক্ত মার্কিন কর্পোরেশনগুলির একটি গ্রুপের অর্থনীতির। ধারণাটি হ'ল যদি কেউ দামের স্প্রেড গ্রহণ করে তবে এটি গড়-পরিণত হওয়া উচিত, কারণ যদিও
কৌশল
কৌশলটি নিম্নলিখিত ধাপে বাস্তবায়ন করা হয়ঃ
- এসপিওয়াই এবং আইডব্লিউএম এর ১ মিনিটের বারগুলি এপ্রিল ২০০৭ থেকে ফেব্রুয়ারী ২০১৪ পর্যন্ত পাওয়া যায়।
- প্রক্রিয়াকরণ - তথ্য সঠিকভাবে সারিবদ্ধ করা হয় এবং অনুপস্থিত বারগুলি একে অপরকে বাদ দেয়।
- স্প্রেড - দুটি ইটিএফের মধ্যে হেজ অনুপাত একটি রোলিং লিনিয়ার রিগ্রেশন গ্রহণ করে গণনা করা হয়। এটি একটি লুকব্যাক উইন্ডো ব্যবহার করে β রিগ্রেশন সহগ হিসাবে সংজ্ঞায়িত করা হয় যা 1 বার এগিয়ে চলে যায় এবং রিগ্রেশন সহগগুলি পুনরায় গণনা করে। সুতরাং বার বি এর জন্য হেজ অনুপাত βi কে বারগুলির জন্য একটি লুকব্যাকের জন্য বি -1 কে থেকে বি -1 পয়েন্ট জুড়ে গণনা করা হয়।
- জেড-স্কোর - স্প্রেডের স্ট্যান্ডার্ড স্কোরটি স্বাভাবিক পদ্ধতিতে গণনা করা হয়। এর অর্থ হ'ল স্প্রেডের (নমুনা) গড়কে বিয়োগ করা এবং স্প্রেডের (নমুনা) স্ট্যান্ডার্ড বিচ্যুতি দ্বারা ভাগ করা। এর যুক্তি হ'ল থ্রেশহোল্ড প্যারামিটারগুলিকে আরও সহজেই ব্যাখ্যা করা যায় কারণ জেড-স্কোর একটি মাত্রাহীন পরিমাণ। এটি কতটা সূক্ষ্ম হতে পারে তা দেখানোর জন্য আমি ইচ্ছাকৃতভাবে গণনার মধ্যে একটি লুকহেড পক্ষপাত চালু করেছি। চেষ্টা করুন এবং এটির জন্য নজর রাখুন!
- ট্রেডস - দীর্ঘ সংকেত তৈরি হয় যখন নেতিবাচক জেড-স্কোর একটি পূর্বনির্ধারিত (বা পোস্ট-অপ্টিমাইজড) প্রান্তিকের নীচে পড়ে, যখন সংক্ষিপ্ত সংকেতগুলি এর বিপরীত হয়। প্রান্তিক জেড-স্কোর অতিরিক্ত প্রান্তিকের নীচে পড়ে যখন প্রান্তিক সংকেত তৈরি হয়। এই কৌশলটির জন্য আমি (কিছুটা স্বতঃস্ফূর্তভাবে) একটি পরম প্রবেশের প্রান্তিক নির্বাচন করেছি।
সম্ভবত কৌশলটি গভীরভাবে বোঝার সর্বোত্তম উপায় হ'ল এটি বাস্তবায়ন করা। নিম্নলিখিত বিভাগে এই গড়-রিভার্টিং কৌশলটি বাস্তবায়নের জন্য একটি সম্পূর্ণ পাইথন কোড (একক ফাইল) বর্ণনা করা হয়েছে। বোঝার জন্য আমি কোডটি উদারভাবে মন্তব্য করেছি।
পাইথন বাস্তবায়ন
সমস্ত পাইথন / পান্ডা টিউটোরিয়ালের মতোই এই টিউটোরিয়ালে বর্ণিত হিসাবে একটি পাইথন গবেষণা পরিবেশ সেটআপ করা প্রয়োজন। একবার সেটআপ হয়ে গেলে, প্রথম কাজটি প্রয়োজনীয় পাইথন লাইব্রেরিগুলি আমদানি করা। এই ব্যাকটেস্টের জন্য ম্যাটপ্লটলিব এবং পান্ডা প্রয়োজন।
আমি যে নির্দিষ্ট লাইব্রেরি সংস্করণ ব্যবহার করছি তা নিম্নরূপঃ
- পাইথন - ২.৭.৩
- NumPy - 1.8.0
- পান্ডা - 0.12.0
- matplotlib - 1.1.0 চলুন লাইব্রেরি আমদানি করি:
# mr_spy_iwm.py
import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd
নিম্নলিখিত ফাংশন create_pairs_dataframe দুটি প্রতীকগুলির অন্তর্দিবসের বারগুলি ধারণকারী দুটি CSV ফাইল আমদানি করে। আমাদের ক্ষেত্রে এটি SPY এবং IWM হবে। এটি তারপরে একটি পৃথক ডেটাফ্রেম জোড়া তৈরি করে, যা উভয় মূল ফাইলের সূচক ব্যবহার করে। যেহেতু তাদের টাইমস্ট্যাম্পগুলি মিসড ট্রেড এবং ত্রুটির কারণে ভিন্ন হতে পারে, তাই এটি গ্যারান্টি দেয় যে আমাদের মিলিত ডেটা থাকবে। এটি পান্ডার মতো ডেটা বিশ্লেষণ লাইব্রেরি ব্যবহারের অন্যতম প্রধান সুবিধা।
# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
"""Creates a pandas DataFrame containing the closing price
of a pair of symbols based on CSV files containing a datetime
stamp and OHLCV data."""
# Open the individual CSV files and read into pandas DataFrames
print "Importing CSV data..."
sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
header=0, index_col=0,
names=['datetime','open','high','low','close','volume','na'])
sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
header=0, index_col=0,
names=['datetime','open','high','low','close','volume','na'])
# Create a pandas DataFrame with the close prices of each symbol
# correctly aligned and dropping missing entries
print "Constructing dual matrix for %s and %s..." % symbols
pairs = pd.DataFrame(index=sym1.index)
pairs['%s_close' % symbols[0].lower()] = sym1['close']
pairs['%s_close' % symbols[1].lower()] = sym2['close']
pairs = pairs.dropna()
return pairs
পরবর্তী পদক্ষেপটি হল এসপিওয়াই এবং আইডব্লিউএম এর মধ্যে রোলিং লিনিয়ার রিগ্রেশন সম্পাদন করা। এই ক্ষেত্রে আইডব্লিউএম হ'ল পূর্বাভাস (
একবার রোলিং বিটা সহগ SPY-IWM এর জন্য লিনিয়ার রিগ্রেশন মডেলের মধ্যে গণনা করা হলে, আমরা এটিকে DataFrame জোড়ায় যোগ করি এবং খালি সারিগুলি বাদ দিই। এটি একটি ট্রিমিং পরিমাপ হিসাবে লুকব্যাকের আকারের সমান প্রথম সেট বার গঠন করে। আমরা তারপরে দুটি ETF এর স্প্রেডটি SPY এবং -βi ইউনিট হিসাবে তৈরি করি IWM। স্পষ্টতই এটি একটি বাস্তবসম্মত পরিস্থিতি নয় কারণ আমরা IWM এর ভগ্নাংশ পরিমাণ নিচ্ছি, যা একটি বাস্তব বাস্তবায়নে সম্ভব নয়।
অবশেষে, আমরা স্প্রেডের জেড-স্কোর তৈরি করি, যা স্প্রেডের গড়কে বিয়োগ করে এবং স্প্রেডের স্ট্যান্ডার্ড ডিভিয়েশন দ্বারা স্বাভাবিককরণ করে গণনা করা হয়। নোট করুন যে এখানে বেশ সূক্ষ্ম লুকহেড পক্ষপাত ঘটেছে। আমি ইচ্ছাকৃতভাবে এটি কোডে রেখেছি কারণ আমি গবেষণায় এই জাতীয় ভুল করা কতটা সহজ তা জোর দিতে চেয়েছিলাম। গড় এবং স্ট্যান্ডার্ড ডিভিয়েশন পুরো স্প্রেড টাইম সিরিজের জন্য গণনা করা হয়। যদি এটি সত্যিকারের historicalতিহাসিক নির্ভুলতা প্রতিফলিত করে তবে এই তথ্যটি উপলভ্য হবে না কারণ এটি নিমজ্জিতভাবে ভবিষ্যতের তথ্য ব্যবহার করে। সুতরাং আমাদের একটি রোলিং গড় এবং স্টেভ ব্যবহার করা উচিত জেড-স্কোর গণনা করতে।
# mr_spy_iwm.py
def calculate_spread_zscore(pairs, symbols, lookback=100):
"""Creates a hedge ratio between the two symbols by calculating
a rolling linear regression with a defined lookback period. This
is then used to create a z-score of the 'spread' between the two
symbols based on a linear combination of the two."""
# Use the pandas Ordinary Least Squares method to fit a rolling
# linear regression between the two closing price time series
print "Fitting the rolling Linear Regression..."
model = pd.ols(y=pairs['%s_close' % symbols[0].lower()],
x=pairs['%s_close' % symbols[1].lower()],
window=lookback)
# Construct the hedge ratio and eliminate the first
# lookback-length empty/NaN period
pairs['hedge_ratio'] = model.beta['x']
pairs = pairs.dropna()
# Create the spread and then a z-score of the spread
print "Creating the spread/zscore columns..."
pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
return pairs
create_long_short_market_signals-এ ট্রেডিং সিগন্যাল তৈরি করা হয়। এইগুলি গণনা করা হয় যখন z-স্কোর নেতিবাচক z-স্কোরকে নেতিবাচকভাবে ছাড়িয়ে যায় এবং যখন z-স্কোর ইতিবাচক z-স্কোরকে ইতিবাচকভাবে ছাড়িয়ে যায় তখন স্প্রেডটি লং করে এবং যখন z-স্কোর ইতিবাচক z-স্কোরকে ছাড়িয়ে যায় তখন স্প্রেডটি সংক্ষিপ্ত করে। exit সিগন্যাল দেওয়া হয় যখন z-স্কোরের পরম মান অন্য (ছোট আকারের) প্রান্তিকের চেয়ে কম বা সমান হয়।
এই পরিস্থিতি অর্জনের জন্য, প্রতিটি বারের জন্য, কৌশলটি
একটি পান্ডা ডেটাফ্রেমের উপর পুনরাবৃত্তি করার জন্য (যা স্বীকার করা হয় না যে এটি একটি সাধারণ অপারেশন নয়) এটি পুনরাবৃত্তি পদ্ধতি ব্যবহার করা প্রয়োজন, যা একটি জেনারেটর সরবরাহ করে যার উপর পুনরাবৃত্তি করা হয়ঃ
# mr_spy_iwm.py
def create_long_short_market_signals(pairs, symbols,
z_entry_threshold=2.0,
z_exit_threshold=1.0):
"""Create the entry/exit signals based on the exceeding of
z_enter_threshold for entering a position and falling below
z_exit_threshold for exiting a position."""
# Calculate when to be long, short and when to exit
pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
# These signals are needed because we need to propagate a
# position forward, i.e. we need to stay long if the zscore
# threshold is less than z_entry_threshold by still greater
# than z_exit_threshold, and vice versa for shorts.
pairs['long_market'] = 0.0
pairs['short_market'] = 0.0
# These variables track whether to be long or short while
# iterating through the bars
long_market = 0
short_market = 0
# Calculates when to actually be "in" the market, i.e. to have a
# long or short position, as well as when not to be.
# Since this is using iterrows to loop over a dataframe, it will
# be significantly less efficient than a vectorised operation,
# i.e. slow!
print "Calculating when to be in the market (long and short)..."
for i, b in enumerate(pairs.iterrows()):
# Calculate longs
if b[1]['longs'] == 1.0:
long_market = 1
# Calculate shorts
if b[1]['shorts'] == 1.0:
short_market = 1
# Calculate exists
if b[1]['exits'] == 1.0:
long_market = 0
short_market = 0
# This directly assigns a 1 or 0 to the long_market/short_market
# columns, such that the strategy knows when to actually stay in!
pairs.ix[i]['long_market'] = long_market
pairs.ix[i]['short_market'] = short_market
return pairs
এই পর্যায়ে আমরা প্রকৃত দীর্ঘ / সংক্ষিপ্ত সংকেত ধারণ করতে জোড়া আপডেট করেছি, যা আমাদের বাজারে থাকা দরকার কিনা তা নির্ধারণ করতে দেয়। এখন আমাদের অবস্থানগুলির বাজার মূল্যের ট্র্যাক রাখতে একটি পোর্টফোলিও তৈরি করতে হবে। প্রথম কাজটি হল একটি অবস্থান কলাম তৈরি করা যা দীর্ঘ এবং সংক্ষিপ্ত সংকেতগুলিকে একত্রিত করে। এটিতে (1,0,−1) থেকে উপাদানগুলির একটি তালিকা থাকবে, যার মধ্যে 1 একটি দীর্ঘ / বাজার অবস্থানকে উপস্থাপন করে, 0 কোনও অবস্থানকে উপস্থাপন করে না (প্রস্থান করা উচিত) এবং -1 একটি সংক্ষিপ্ত / বাজার অবস্থানকে উপস্থাপন করে। সিম 1 এবং সিম 2 কলামগুলি প্রতিটি বারের শেষে এসপিওয়াই এবং আইডাব্লুএম অবস্থানের বাজার মানগুলি উপস্থাপন করে।
একবার ইটিএফ বাজার মূল্য তৈরি হয়ে গেলে, আমরা প্রতিটি বার শেষে মোট বাজার মূল্য উত্পাদন করতে তাদের যোগ করি। এটি তারপরে সেই সিরিজ অবজেক্টের জন্য pct_change পদ্ধতি দ্বারা রিটার্ন স্ট্রিমে পরিণত হয়। পরবর্তী কোড লাইনগুলি খারাপ এন্ট্রিগুলি (NaN এবং inf উপাদান) পরিষ্কার করে এবং অবশেষে পূর্ণ ইক্যুইটি বক্ররেখা গণনা করে।
# mr_spy_iwm.py
def create_portfolio_returns(pairs, symbols):
"""Creates a portfolio pandas DataFrame which keeps track of
the account equity and ultimately generates an equity curve.
This can be used to generate drawdown and risk/reward ratios."""
# Convenience variables for symbols
sym1 = symbols[0].lower()
sym2 = symbols[1].lower()
# Construct the portfolio object with positions information
# Note that minuses to keep track of shorts!
print "Constructing a portfolio..."
portfolio = pd.DataFrame(index=pairs.index)
portfolio['positions'] = pairs['long_market'] - pairs['short_market']
portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
portfolio['total'] = portfolio[sym1] + portfolio[sym2]
# Construct a percentage returns stream and eliminate all
# of the NaN and -inf/+inf cells
print "Constructing the equity curve..."
portfolio['returns'] = portfolio['total'].pct_change()
portfolio['returns'].fillna(0.0, inplace=True)
portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
portfolio['returns'].replace(-1.0, 0.0, inplace=True)
# Calculate the full equity curve
portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
return portfolio
দ্যপ্রধানইনট্রাডে CSV ফাইলগুলি ডেটাডির পাথে অবস্থিত। আপনার নির্দিষ্ট ডিরেক্টরিতে নির্দেশ করার জন্য নীচের কোডটি সংশোধন করতে ভুলবেন না।
পুনর্বিবেচনার সময়কালে কৌশলটি কতটা সংবেদনশীল তা নির্ধারণ করার জন্য পুনর্বিবেচনার পরিসীমাটির জন্য একটি পারফরম্যান্স মেট্রিক গণনা করা প্রয়োজন। আমি পারফরম্যান্স পরিমাপ হিসাবে পোর্টফোলিওর চূড়ান্ত মোট শতাংশ রিটার্ন এবং পুনর্বিবেচনার পরিসীমাটি [50,200] এ 10 এর বৃদ্ধি সহ বেছে নিয়েছি। আপনি নিম্নলিখিত কোডে দেখতে পারেন যে পূর্ববর্তী ফাংশনগুলি এই পরিসীমা জুড়ে একটি ফর লুপে আবৃত রয়েছে, অন্যান্য থ্রেশহোল্ডগুলি স্থির রাখা হয়েছে। চূড়ান্ত কাজটি হল পুনর্বিবেচনার বনাম রিটার্নের একটি লাইন চার্ট তৈরি করতে ম্যাটপ্লটলিব ব্যবহার করাঃ
# mr_spy_iwm.py
if __name__ == "__main__":
datadir = '/your/path/to/data/' # Change this to reflect your data path!
symbols = ('SPY', 'IWM')
lookbacks = range(50, 210, 10)
returns = []
# Adjust lookback period from 50 to 200 in increments
# of 10 in order to produce sensitivities
for lb in lookbacks:
print "Calculating lookback=%s..." % lb
pairs = create_pairs_dataframe(datadir, symbols)
pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
pairs = create_long_short_market_signals(pairs, symbols,
z_entry_threshold=2.0,
z_exit_threshold=1.0)
portfolio = create_portfolio_returns(pairs, symbols)
returns.append(portfolio.ix[-1]['returns'])
print "Plot the lookback-performance scatterchart..."
plt.plot(lookbacks, returns, '-o')
plt.show()
lookback period vs returns এর চার্ট এখন দেখা যাবে। মনে রাখবেন যে lookback এর চারপাশে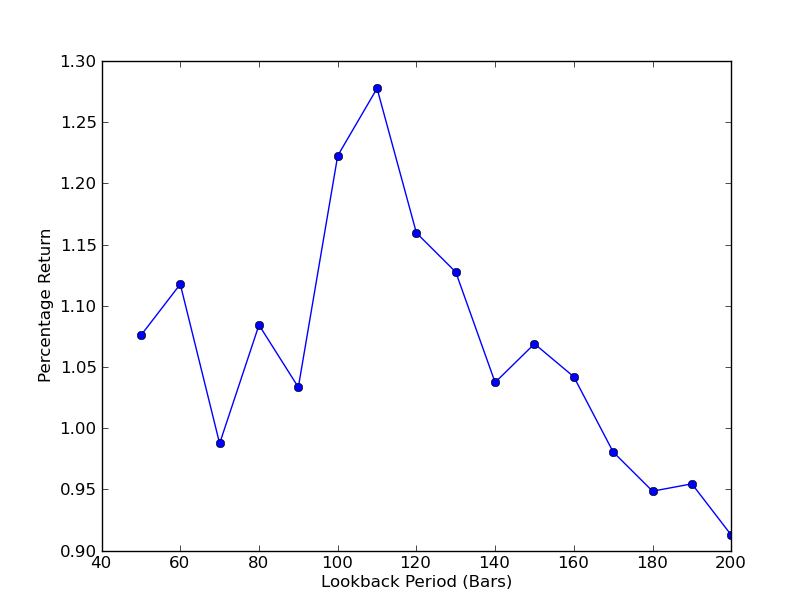 
এসপিওয়াই-আইডব্লিউএম লিনিয়ার রিগ্রেশন হেজিং রেসিও রিপ্লেক্স পিরিয়ড সংবেদনশীলতা বিশ্লেষণ
কোন ব্যাকটেস্টিং নিবন্ধটি একটি উপরের দিকে ঢালযুক্ত ইক্যুইটি বক্ররেখা ছাড়া সম্পূর্ণ হবে না! সুতরাং আপনি যদি সময় বনাম সমষ্টিগত রিটার্নের একটি বক্ররেখা প্লট করতে চান তবে আপনি নিম্নলিখিত কোডটি ব্যবহার করতে পারেন। এটি লুকব্যাক পরামিতি অধ্যয়ন থেকে উত্পন্ন চূড়ান্ত পোর্টফোলিওটি প্লট করবে। সুতরাং আপনি কোন চার্টটি ভিজ্যুয়ালাইজ করতে চান তার উপর নির্ভর করে লুকব্যাকটি চয়ন করা প্রয়োজন হবে। চার্টটি তুলনা করতে সহায়তা করার জন্য একই সময়ের মধ্যে এসপিওয়াইয়ের রিটার্নগুলিও প্লট করেঃ
# mr_spy_iwm.py
# This is still within the main function
print "Plotting the performance charts..."
fig = plt.figure()
fig.patch.set_facecolor('white')
ax1 = fig.add_subplot(211, ylabel='%s growth (%%)' % symbols[0])
(pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
portfolio['returns'].plot(ax=ax2, lw=2.)
fig.show()
নিম্নলিখিত শেয়ারের কার্ভ চার্টটি ১০০ দিনের ব্যাকপ্যাক সময়ের জন্যঃ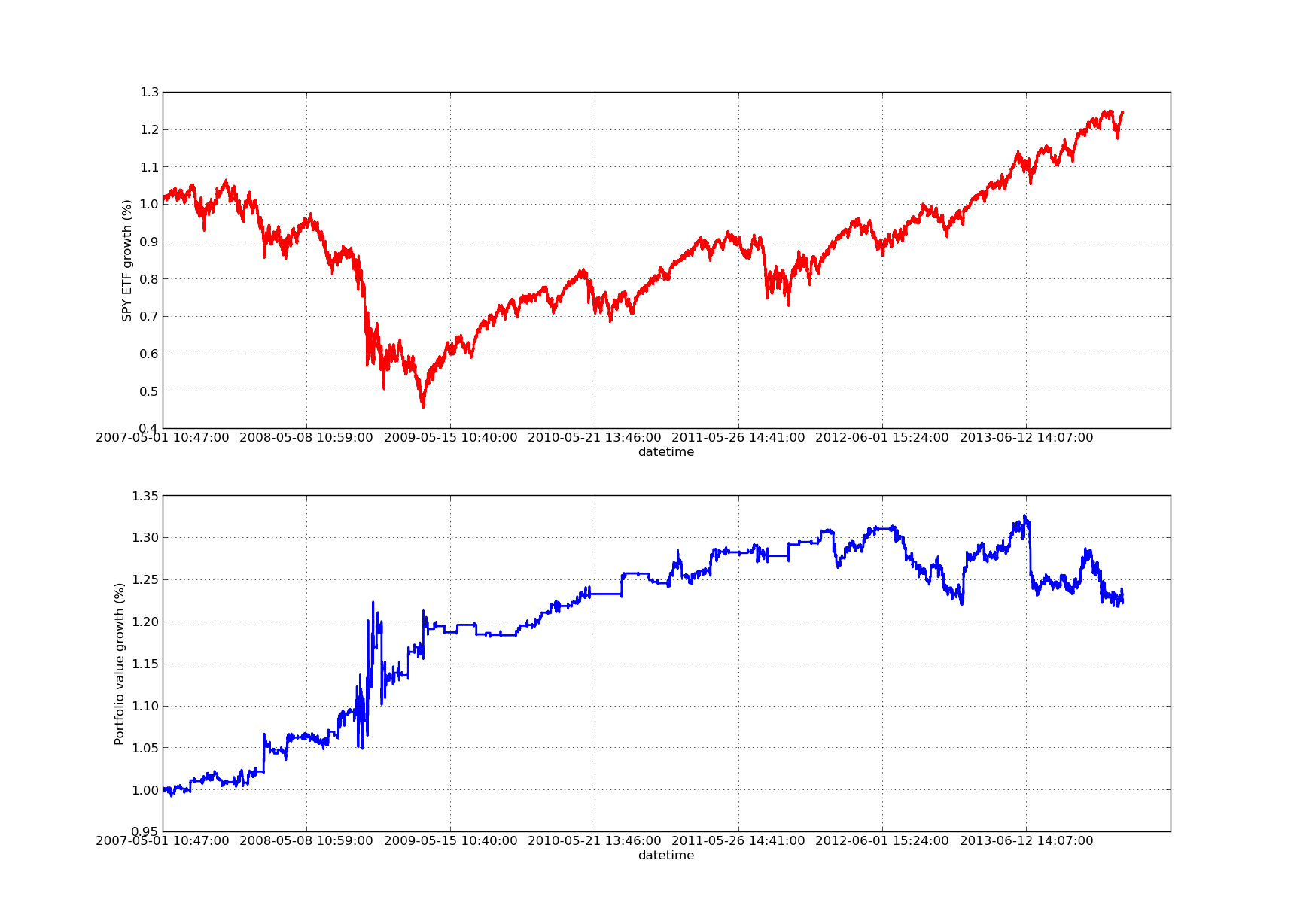
এসপিওয়াই-আইডব্লিউএম লিনিয়ার রিগ্রেশন হেজিং রেসিও রিপ্লেক্স পিরিয়ড সংবেদনশীলতা বিশ্লেষণ
নোট করুন যে ২০০৯ সালে আর্থিক সঙ্কটের সময় এসপিওয়াইয়ের ব্যবহার উল্লেখযোগ্য ছিল। এই পর্যায়ে কৌশলটিও একটি অস্থির সময়কাল ছিল। এছাড়াও নোট করুন যে এই সময়ে এসপিওয়াইয়ের প্রবল প্রবণতার প্রকৃতির কারণে গত বছরে পারফরম্যান্স কিছুটা খারাপ হয়েছে, যা এসএন্ডপি 500 সূচককে প্রতিফলিত করে।
লক্ষ্য করুন যে স্প্রেডের জেড-স্কোর গণনা করার সময় আমাদের এখনও লুকহেড পক্ষপাত বিবেচনা করতে হবে। তদতিরিক্ত, এই সমস্ত গণনা লেনদেনের ব্যয় ছাড়াই সম্পন্ন করা হয়েছে। এই কৌশলটি অবশ্যই এই কারণগুলি বিবেচনা করার পরে খুব খারাপভাবে সম্পাদন করবে। ফি, বিড / অ্যাসক স্প্রেড এবং স্লিপজ বর্তমানে সমস্ত অ্যাকাউন্ট করা হয় না। এছাড়াও কৌশলটি ইটিএফগুলির ভগ্নাংশ ইউনিটগুলিতে বাণিজ্য করছে, যা খুব অবাস্তব।
পরবর্তী প্রবন্ধে আমরা একটি আরো পরিশীলিত ইভেন্ট-চালিত ব্যাকটেস্টার তৈরি করব যা এই কারণগুলি বিবেচনা করবে এবং আমাদের ইক্যুইটি কার্ভ এবং পারফরম্যান্স মেট্রিকগুলিতে আমাদের উল্লেখযোগ্যভাবে বেশি আস্থা দেবে।
- বিটমেক্স এক্সচেঞ্জ এপিআই নোট
- ছোট্ট প্রশ্ন, কিভাবে ব্লকলি ভিজ্যুয়ালাইজেশন প্রোগ্রামিং দিয়ে বাজারের নিচে লেনদেনের তালিকা তৈরি করা যায়?
- উদ্ভাবক ডিজিটাল মুদ্রা পরিমাণিকরণ প্ল্যাটফর্ম websocket ব্যবহারের গাইড ((ডায়াল ফাংশন আপগ্রেড করার পরে বিস্তারিত)
- Robotdetail ইন্টারফেসের প্যারামিটার 3 পাওয়া অদ্ভুত।
- কিভাবে নতুনরা রাস্তা দিয়ে যেতে পারে, কিভাবে প্রবণতা ধরতে পারে এবং লাভ দীর্ঘস্থায়ী করতে পারে?
- টাইম সিরিজ বিশ্লেষণের জন্য শিক্ষানবিশদের গাইড
- পান্ডার সাথে পাইথনে এসএন্ডপি 500 এর জন্য পূর্বাভাস কৌশল ব্যাকটেস্টিং
কবে ছাড়বেন তা সবসময় বুঝুন ৬টি প্রস্থান কৌশল - এফএমজেড পাবলিক ইন্টারেক্টিভ
- কোয়ান্ট ফান্ডের বিভিন্ন প্রকার কি?
- পাণ্ডাসহ পাইথনে একটি চলমান গড় ক্রসওভার ব্যাকটেস্টিং
- অ্যালগরিদমিক ট্রেডিং কৌশলগুলি কীভাবে সনাক্ত করবেন
- পাইথনের সাথে ইভেন্ট-চালিত ব্যাকটেস্টিং - অংশ VIII
- ব্লকচেইন পরিমাণগত বিনিয়োগ সিরিজ - গতিশীল ভারসাম্য কৌশল
- পাইথনের সাথে ইভেন্ট-চালিত ব্যাকটেস্টিং - অংশ VII
- পাইথনের সাথে ইভেন্ট-চালিত ব্যাকটেস্টিং - অংশ VI
- পাইথনের সাথে ইভেন্ট-চালিত ব্যাকটেস্টিং - পার্ট V
- পাইথনের সাথে ইভেন্ট-চালিত ব্যাকটেস্টিং - অংশ IV
- পাইথনের সাথে ইভেন্ট-ড্রাইভড ব্যাকটেস্টিং - পার্ট III
- পাইথনের সাথে ইভেন্ট-ড্রাইভড ব্যাকটেস্টিং - পার্ট II