গণিত এবং জুয়া খেলা (১)

গণিত এবং জুয়া

• আমরা জানি যে জুয়া খেলাটি সম্ভাবনার খেলা, এবং কিছু অদ্ভুত জুয়া ফলাফল গণিতবিদ পাস্কাল এবং মহান গণিতবিদ ফর্ম্যাট এর আগ্রহকে জাগিয়ে তুলেছিল, যারা চিঠিপত্রের মাধ্যমে সম্ভাব্যতার তত্ত্বের কিছু নীতি প্রস্তাব করেছিল, যার ফলে সম্ভাব্যতার তত্ত্ব তৈরি হয়েছিল। আজ আমরা কয়েকটি জুয়া খেলার মধ্যে সম্ভাব্যতার কৌতূহল সম্পর্কে জানব।

• ১, নিখুঁত জুয়া খেলা

এনবিএ দল লেকার্স এবং বালকস একটি ম্যাচ আছে, উভয় দলের অনুগত অনুরাগীরা, তাদের ডেকে আনুন ময়ূর ময়ূর এবং বালকস বাউল। অবশ্যই অনুরাগীরা মনে করেন যে তাদের সমর্থিত দলটি জয়ের সম্ভাবনা বেশি, তাই তারা আপনার সাথে বাজি ধরতে ইচ্ছুক। ধরুন ময়ূর ময়ূর মনে করেন যে লেকারস জয়ের সম্ভাবনা p, বালকস ময়ূর মনে করেন যে বালকস জয়ের সম্ভাবনা q, p এবং q উভয়ই 50% এর চেয়ে বেশি হওয়া উচিত। পরবর্তী অংশটি আকর্ষণীয়, আমরা সর্বদা সহজেই একটি পদ্ধতি ডিজাইন করতে পারি, যথাক্রমে ময়ূর ময়ূর এবং বালকস ময়ূরদের সাথে বাজি ধরতে পারি, তবে ফলাফল যাই হোক না কেন, আমরা স্থিতিশীল।

পদ্ধতিটি হলঃ আমরা একে অপরের সাথে একই জুটি বাজি ধরছি, যদি আমরা জিতে থাকি তবে y, যদি আমরা হেরে যাই তবে x, যদি y > x হয় তবে আমরা জিতব। এবং x এবং y কেবলমাত্র নিম্নলিখিত দুটি সহজ অসমতা পূরণ করতে হবে, জুটি বাজি এবং জুটি বাজি প্রত্যাশিত আয় ইতিবাচক হবে, আমাদের সাথে বাজি ধরবেঃ

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

y>x এর সীমাবদ্ধতার সাথে, অঙ্কিত চিত্রটি তিনটি সোজা রেখা দ্বারা বেষ্টিত অঞ্চল, যার মধ্যে যে কোনও একটি বিন্দুর জন্য স্থানাঙ্ক মান ((x,y) একটি বিজয়ী সমাধান। যদি p>q হয় তবে সমাধানটি নীচের চিত্রের নীল অংশঃ

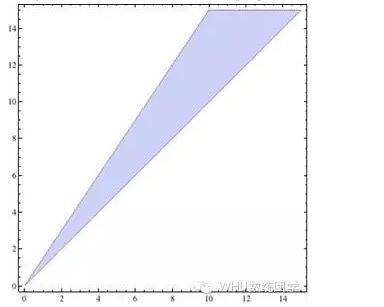
এই প্রশ্নটি নিখুঁতভাবে সমাধান করা হয়েছে বলে মনে হচ্ছে, কিন্তু একটি সন্দেহ আছে, যা আমি বিশ্বাস করি পাঠক শীঘ্রই এর হাস্যকরতা দেখতে পাবেনঃ ময়ূর বা ময়ূর ময়ূর উভয়েরই প্রত্যাশা সঠিক, অর্থাৎ দীর্ঘমেয়াদে তারা অর্থ উপার্জন করবে, এবং আমরা স্থিতিশীল, এত টাকা কোথা থেকে এসেছে, কিভাবে সবাই অর্থ উপার্জন করতে পারে?

• দুই, তিন কার্ডের জালিয়াতি

  

এটি আরেকটি চতুর প্যারাডক্স, যেখানে আমরা প্রথমে তিনটি কার্ড প্রস্তুত করি, যার মধ্যে একটি হল কালো, দ্বিতীয়টি হল লাল এবং তৃতীয়টি হল একপাশে কালো এবং দ্বিতীয়টি হল লাল। তারপর কার্ডটি একটি বাক্সে রাখুন, এটিকে ঝাঁকুনি দিন এবং আপনার প্রতিপক্ষকে টেবিলে একটি সমতল টেনে আনুন। তারপরে তার মুখোমুখি মুখটি একই রঙের এবং ইতিবাচক। এই প্যারাডক্সটি দেখতে ন্যায্য বলে মনে হচ্ছে, উদাহরণস্বরূপ, যদি একটি পৃষ্ঠটি কালো হয় তবে কার্ডটি 1 বা 3 নয়, এবং বিপরীতটি কালো বা লাল নয়, এবং স্বজ্ঞাতভাবে প্রতিটি সম্ভাবনা 1/2।

আসলে আমাদের জেতার সম্ভাবনা 1/2 নয়, বরং 2/3। এই প্যাকেজের সবচেয়ে বিভ্রান্তিকর অংশ হল কার্ডের ডাবল-সাইড ডাবল-সাইড। খেলোয়াড়রা 3 টি কার্ডের পরিবর্তে 6 টি মুখ, 3 টি কালো মুখ এবং 3 টি লাল মুখ টানছে। আমরা এই 6 টি মুখকে A, B, C, D, E, F:

যখন খেলোয়াড়রা কালো দিকে টানেন, তখন তিনটি সম্ভাব্য পরিস্থিতি A,C,D ইত্যাদি, তাদের পিছনে D,F,A, এবং কালো 2/3 পরিস্থিতি।

এই প্রশ্নটি প্রথম ১৮৮৯ সালে ফরাসি গণিতবিদ জোসেফ লুই ফ্রান্সিস বারট্র্যান্ডের দ্বারা উত্থাপিত হয়েছিল, এবং এটি বারট্র্যান্ডের বাক্সের বিদ্রূপ নামেও পরিচিত কারণ এর ফলাফলগুলি অপ্রত্যাশিত ছিল। ১৯৫০ সালে আমেরিকান গণিতবিদ ওয়ারেন ওয়েভার উপরের কার্ডের খেলাটি চালু করেছিলেন, যা মার্টিন গার্ডনার তিন কার্ডের জালিয়াতি বলে অভিহিত করেছিলেন।

• ৩, অসাধারণ একটি বার্গার A।

  

  কখনও কখনও আমরা জুয়া খেলার শুরুতে পানি ফেলি, প্রথমে অন্যকে কিছু টাকা দিতে বলি, লম্বা লাইন লাগিয়ে বড় মাছ ধরতে বলি, এবং শেষ পর্যন্ত একটি নেট শেষ হয়। নীচে একটি দুর্দান্ত উদাহরণ রয়েছে। চারজন লোক ব্রিজ খেলছে, আমি প্রথমে বলিঃ "আচ্ছা, একটি টুকরো খেলুন, আমার এখন একটি এ আছে, আপনি কি অনুমান করেন যে আমার আরও এ আছে?

  অনেকেরই মনে হয় যে, দুইটি মুরগি একে অপরের থেকে আলাদা নয় এবং একটি মরিচ যোগ করা ঠিক নয়। কিন্তু তাদের মধ্যে পার্থক্য অবিশ্বাস্য। আসুন প্রথমে প্রথম মুরগির সম্ভাব্যতা গণনা করিঃ

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：
  
  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%
  

  এই সময় আমি নিজেকে A দিয়ে বাজি ধরতে চেয়েছিলাম, এটি হারানো সহজ ছিল। তবে প্রথম জয়ের জয়ের পরে, সবাই বাজি ধরার ইচ্ছা প্রকাশ করেছিল, দ্বিতীয় জয়ের দিকে তাকিয়ে তারা পোশাক পরিবর্তন করেনি, তারা বাজি বাড়িয়েছিল, তারপরে আমি আর A পাইনি, আমরা এখনই হেরেছি। নীচে আমরা দেখতে পাব যে দ্বিতীয় জয়ের সম্ভাবনা অনেক আলাদাঃ

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：
  
  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。
  

WHU অ্যানিম্যাট্রিক্স থেকে পুনর্নির্দেশিত