৮টি মেশিন লার্নিং অ্যালগরিদমের তুলনা
 0
0
 6487
6487
৮টি মেশিন লার্নিং অ্যালগরিদমের তুলনা
এই নিবন্ধটি মূলত নিম্নলিখিত কয়েকটি সাধারণ অ্যালগরিদমের অভিযোজন পরিস্থিতি এবং তাদের সুবিধা এবং অসুবিধাগুলি পর্যালোচনা করে।
মেশিন লার্নিং এর অনেকগুলো অ্যালগরিদম আছে, যেমন শ্রেণীবিভাগ, রিগ্রেশন, ক্লাস্টারিং, সুপারিশ, ইমেজ রিকগনিশন ইত্যাদি, তাই একটি উপযুক্ত অ্যালগরিদম খুঁজে বের করা সত্যিই কঠিন, তাই আমরা সাধারণত অনুপ্রেরণামূলক লার্নিং পদ্ধতি ব্যবহার করি।
সাধারণত শুরুতে আমরা সাধারণভাবে স্বীকৃত অ্যালগরিদম যেমন এসভিএম, জিবিডিটি, অ্যাডাবুস্ট, ডিপ লার্নিং এবং নিউরাল নেটওয়ার্ক পছন্দ করি।
যদি আপনি সঠিকতা সম্পর্কে চিন্তা করেন, তাহলে সবচেয়ে ভালো উপায় হল ক্রস-ভ্যালিডেশন (cross-validation) এর মাধ্যমে প্রতিটি অ্যালগরিদমকে এক এক করে পরীক্ষা করা, তুলনা করা, তারপর প্যারামিটারগুলি সামঞ্জস্য করা যাতে প্রতিটি অ্যালগরিদম সর্বোত্তম সমাধান পায়, এবং শেষ পর্যন্ত সেরাটি বেছে নেওয়া।
কিন্তু যদি আপনি শুধু আপনার সমস্যার সমাধানের জন্য যথেষ্ট ভাল একটি অ্যালগরিদম খুঁজছেন, অথবা এখানে কিছু টিপস রয়েছে যা আপনি ব্যবহার করতে পারেন, তাহলে নিচে প্রতিটি অ্যালগরিদমের সুবিধা এবং অসুবিধাগুলি বিশ্লেষণ করা হল, যা আমাদের পক্ষে এটি বেছে নেওয়া সহজ করে তোলে।
- ## বিভেদ ও বৈষম্য
পরিসংখ্যানশাস্ত্রে, একটি মডেলের ভাল বা খারাপের পরিমাপ করা হয় বিভেদ এবং বৈষম্যের উপর ভিত্তি করে, তাই আসুন আমরা বিভেদ এবং বৈষম্যকে সাধারণীকরণ করিঃ
বিচ্যুতিঃ এটি পূর্বাভাস মানের (অনুমান মান) প্রত্যাশিত E এবং প্রকৃত মান Y এর মধ্যে পার্থক্য বর্ণনা করে। বিচ্যুতি যত বেশি, তত বেশি সত্য তথ্য থেকে বিচ্যুত হয়।
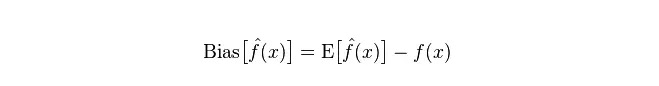
বিভাজক: বিভাজকটি হল পূর্বাভাস মান P-এর পরিবর্তনের পরিধি এবং বিভাজকটির মাত্রা, যা পূর্বাভাস মানের বিভাজক, অর্থাৎ তার প্রত্যাশিত মান E-র দূরত্ব। বিভাজকটি যত বড় হবে, তথ্যের বন্টন তত বেশি বিচ্ছিন্ন হবে।
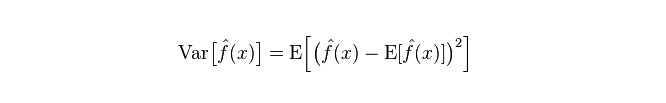
মডেলের প্রকৃত ত্রুটি হল এই দুইটির সমষ্টি, যেমন নিচে দেখানো হয়েছেঃ
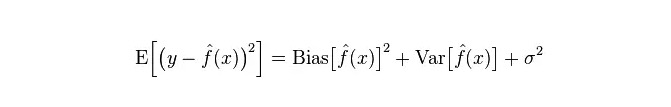
যদি ছোট প্রশিক্ষণ সেট হয়, উচ্চ বিচ্যুতি / নিম্ন বিচ্যুতি শ্রেণিবিন্যাসকারী (যেমন, সরল বেয়েজিয়ান এনবি) নিম্ন বিচ্যুতি / উচ্চ বিচ্যুতি বড় শ্রেণিবিন্যাসকারী (যেমন, কেএনএন) এর চেয়ে বেশি সুবিধাজনক হবে, কারণ পরেরটি অতিরিক্ত ফিট হবে।
তবে, আপনার প্রশিক্ষণ সেটটি বাড়ার সাথে সাথে মডেলটি মূল তথ্যের জন্য আরও ভাল ভবিষ্যদ্বাণী করতে সক্ষম হয়, বিভ্রান্তি হ্রাস পায়, এই মুহুর্তে কম বিভ্রান্তি / উচ্চতর বিভ্রান্তি শ্রেণিবিন্যাসকারীরা ধীরে ধীরে তাদের সুবিধা প্রদর্শন করে (কারণ তাদের কাছে কম ক্রমান্বয়ে বিভ্রান্তি রয়েছে), এই মুহুর্তে উচ্চতর বিভ্রান্তি শ্রেণিবিন্যাসকারীরা সঠিক মডেল সরবরাহ করতে যথেষ্ট নয়।
অবশ্যই, আপনি এটিকে জেনারেটর মডেল (NB) এবং ডিসক্রিপশন মডেল (KNN) এর মধ্যে পার্থক্য হিসাবেও বিবেচনা করতে পারেন।
- ## এই প্রশ্নের জবাবে, “কেন বেজোসকে উচ্চ-বিপরীত-নিম্ন-বিপরীত বলা হয়?
তিনি বলেনঃ
প্রথমত, ধরুন আপনি ট্রেনিং সেট এবং টেস্ট সেটের মধ্যে সম্পর্ক জানেন। সহজ কথায় বলতে গেলে, আমরা ট্রেনিং সেটে একটি মডেল শিখব এবং টেস্ট সেটটি ব্যবহার করব।
কিন্তু অনেক সময়, আমরা কেবলমাত্র অনুমান করতে পারি যে পরীক্ষার সেট এবং প্রশিক্ষণ সেট একই ডেটা বন্টনের সাথে সামঞ্জস্যপূর্ণ, কিন্তু আসল পরীক্ষার ডেটা পাওয়া যায় না। তাহলে প্রশিক্ষণের ত্রুটি হার দেখে পরীক্ষার ত্রুটি হারটি কীভাবে পরিমাপ করা যায়?
যেহেতু প্রশিক্ষণের নমুনা খুব কম (অন্তত পর্যাপ্ত নয়), তাই প্রশিক্ষণের মাধ্যমে প্রাপ্ত মডেলটি সর্বদা সত্য নয়। (এটি প্রশিক্ষণের উপর 100% সঠিক হলেও এটি সত্যিকারের ডেটা বন্টন আঁকতে পারে না। আমাদের লক্ষ্য সত্যিকারের ডেটা বন্টন আঁকতে হবে, কেবলমাত্র প্রশিক্ষণের সীমাবদ্ধ ডেটা পয়েন্টগুলি আঁকতে হবে না) ।
এবং, বাস্তবে, প্রশিক্ষণের নমুনাগুলি প্রায়শই কিছুটা গোলমালের ত্রুটি থাকে, তাই যদি প্রশিক্ষণ সেটের নিখুঁততার জন্য খুব জটিল মডেল ব্যবহার করা হয় তবে মডেলটি প্রশিক্ষণ সেটের মধ্যে থাকা ত্রুটিগুলিকে সত্যিকারের ডেটা বিতরণের বৈশিষ্ট্য হিসাবে বিবেচনা করতে পারে, যার ফলে ভুল ডেটা বিতরণ অনুমান করা হয়।
এই ক্ষেত্রে, সত্যিকারের পরীক্ষার সেটটি ভুল হয়ে যায় (এই ঘটনাটিকে ফিট বলা হয়) । তবে খুব সহজ মডেল ব্যবহার করা যাবে না, অন্যথায় যখন ডেটা বিতরণ আরও জটিল হয়, তখন মডেলটি ডেটা বিতরণ চিত্রিত করার পক্ষে যথেষ্ট নয় (এটি প্রশিক্ষণ সেটগুলিতেও উচ্চ ত্রুটি হার হিসাবে প্রতিফলিত হয়, এই ঘটনাটি কম ফিট) ।
ওভার-ফিট ইঙ্গিত দেয় যে মডেলটি সত্যিকারের ডেটা বন্টনের চেয়ে জটিল, এবং কম ফিট ইঙ্গিত দেয় যে মডেলটি সত্যিকারের ডেটা বন্টনের চেয়ে সহজ।
পরিসংখ্যান শিক্ষার কাঠামোর মধ্যে, যখন আমরা মডেলের জটিলতা চিত্রিত করি, তখন এই মতামতটি রয়েছে যে ত্রুটি = পক্ষপাত + বৈচিত্র্য। এখানে ত্রুটিটি সম্ভবত মডেলের পূর্বাভাস ত্রুটি হিসাবে বোঝা যায়, এটি দুটি অংশে গঠিত, একটি অংশটি মডেলটি খুব সহজ বলে অনুমান করা অযৌক্তিক অংশ (দ্বিতীয় অংশটি খুব জটিল কারণ মডেলটি আরও বড় পরিবর্তনের স্থান এবং অনিশ্চয়তা (দ্বিতীয় অংশ) ।
সুতরাং, এটা সহজেই সহজ বেয়েজ বিশ্লেষণ করা যায়। এটির সহজ অনুমান যে প্রতিটি তথ্যের মধ্যে সম্পর্কহীনতা রয়েছে, একটি মারাত্মকভাবে সরলীকৃত মডেল। সুতরাং, এই ধরনের একটি সহজ মডেলের জন্য, বেশিরভাগ ক্ষেত্রে, বিয়াস অংশটি ভেরিয়েন্স অংশের চেয়ে বড় হবে, অর্থাৎ উচ্চ বিচ্যুতি এবং কম বৈচিত্র্য।
বাস্তবে, ত্রুটিকে যতটা সম্ভব ছোট করার জন্য, আমাদের মডেল নির্বাচন করার সময় বায়াস এবং বৈচিত্র্যের অনুপাতের ভারসাম্য বজায় রাখতে হবে, অর্থাৎ ওভার-ফিটিং এবং আন্ডার-ফিটিংয়ের ভারসাম্য বজায় রাখতে হবে।
নিম্নলিখিত চিত্রটি বিশ্লেষণ করে বোঝা যায় যে বিভেদ এবং বর্গক্ষেত্রের পার্থক্য মডেলের জটিলতার সাথে সম্পর্কিতঃ
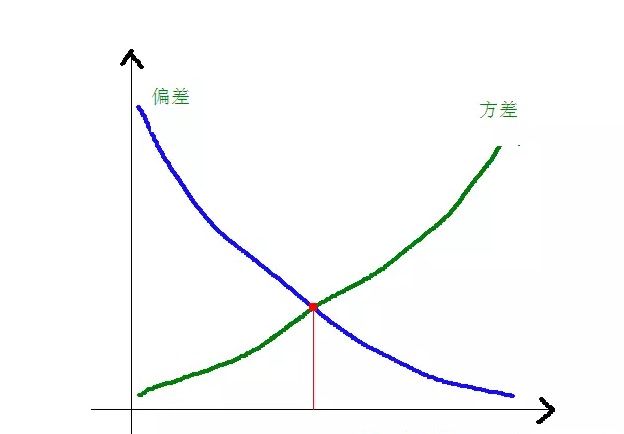
মডেলের জটিলতা বাড়ার সাথে সাথে, বিভেদটি ছোট হয়ে যায় এবং পার্থক্যটি বড় হয়।
-
সাধারণ অ্যালগরিদমের সুবিধা এবং অসুবিধা
- ### ১. প্রক্সি বেয়েস
সরল বেয়েজিয়ানদের মধ্যে একটি হল জেনারেটর মডেল (যদিও জেনারেটর মডেল এবং ডিসিশনাল মডেলের ক্ষেত্রে, এটি মূলত জয়েন্ট ডিস্ট্রিবিউশনের জন্য অনুরোধ করা হয় কিনা), খুব সহজ, আপনি কেবল গণনার একটি গুচ্ছ করেন।
যদি শর্তসাপেক্ষ স্বাধীনতার অনুমান করা হয় (একটি আরও কঠোর শর্ত), সহজ Bayesian শ্রেণীবিভাগের ঘূর্ণন গতি বিচারক মডেলের চেয়ে দ্রুত হবে, যেমন লজিক্যাল রিগ্রেশন, তাই আপনি শুধুমাত্র কম প্রশিক্ষণ ডেটা প্রয়োজন। এমনকি যদি NB শর্তসাপেক্ষ স্বাধীনতার অনুমানটি সত্য না হয়, NB শ্রেণীবিভাগ বাস্তবে এখনও ভাল কাজ করে।
এর প্রধান ত্রুটি হচ্ছে এটি চরিত্রের মধ্যে পারস্পরিক ক্রিয়াশীলতা শিখতে পারে না। mRMR এর R হল চরিত্রের অপ্রয়োজনীয়তা। উদাহরণস্বরূপ, আপনি ব্র্যাড পিট এবং টম ক্রুজ এর সিনেমা পছন্দ করেন, কিন্তু আপনি তাদের সিনেমা পছন্দ করেন না তা শিখতে পারে না।
সুবিধাসমূহঃ
সরল বেয়েজ মডেলটি ধ্রুপদী গাণিতিক তত্ত্ব থেকে উদ্ভূত, এর একটি শক্ত গাণিতিক ভিত্তি এবং একটি স্থিতিশীল শ্রেণিবদ্ধকরণ দক্ষতা রয়েছে। ছোট আকারের ডেটাতে ভাল পারফরম্যান্স, বহু-শ্রেণীর কাজগুলি একসাথে পরিচালনা করতে পারে, ইনক্রিমেটিভ প্রশিক্ষণের জন্য উপযুক্ত; অনুপস্থিত তথ্যের প্রতি কম সংবেদনশীল, এবং অ্যালগরিদমটি সহজ, যা প্রায়শই পাঠ্য শ্রেণিবিন্যাসে ব্যবহৃত হয়। ত্রুটিঃ
এই ক্ষেত্রে, একটি প্রাক-সম্ভাব্যতা গণনা করা প্রয়োজন। শ্রেণিবিন্যাসের সিদ্ধান্তে ত্রুটির হার; ইনপুট ডেটা এক্সপ্রেশন ফর্ম্যাটে সংবেদনশীল।
- ### ২. লজিক্যাল রিগ্রেশন
এখানে অনেকগুলো পদ্ধতি আছে যেগুলোকে আপনি নিয়মীয়াকরণ করতে পারেন (L0, L1, L2, ইত্যাদি) এবং আপনাকে আপনার বৈশিষ্ট্যগুলো প্রাসঙ্গিক কিনা তা নিয়ে চিন্তিত হতে হবে না, যেমনটি আপনি সহজ বেয়েজ মডেলের ক্ষেত্রে করেন।
সিদ্ধান্ত গাছ এবং এসভিএম মেশিনের তুলনায় আপনি একটি ভাল সম্ভাব্যতা ব্যাখ্যা পাবেন এবং আপনি সহজেই নতুন ডেটা ব্যবহার করে মডেলটি আপডেট করতে পারেন (অনলাইন গ্রেডিয়েন্ট অবতরণ অ্যালগরিদম ব্যবহার করে) ।
যদি আপনার একটি সম্ভাব্যতা আর্কিটেকচার প্রয়োজন হয় (যেমন, সহজেই শ্রেণীবিন্যাসের থ্রেশহোল্ডগুলি নিয়ন্ত্রণ করা, অনিশ্চয়তা নির্দেশ করা, বা আস্থা ব্যবধান অর্জন করা), অথবা আপনি যদি পরে মডেলটিতে আরও প্রশিক্ষণ ডেটা দ্রুত সংহত করতে চান তবে এটি ব্যবহার করুন।
সিগময়েড ফাংশনঃ
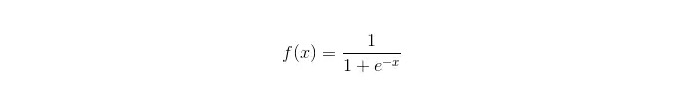
সুবিধাসমূহঃ এটি সহজ এবং ব্যাপকভাবে শিল্পের ক্ষেত্রে প্রয়োগ করা হয়; এই ধরনের শ্রেণিবিন্যাসের জন্য কম্পিউটারের পরিমাণ খুবই কম, গতি অনেক বেশি এবং সংরক্ষণের ক্ষমতা কম। সহজেই পরিদর্শন করা নমুনার সম্ভাব্যতা স্কোর; লজিক্যাল রিগ্রেশন এর ক্ষেত্রে, মাল্টিপল কমনোলিওনিটি সমস্যা নয়, এটি L2 রীতিমতো করার সাথে একত্রে সমাধান করা যেতে পারে; ত্রুটিঃ যখন বৈশিষ্ট্য স্পেস বড়, লজিকাল রিগ্রেশন খুব ভাল কাজ করে না; প্রায়শই ভুল মিলিত হয়, সাধারণত সঠিকতা খুব বেশি নয় অনেকগুলি বৈশিষ্ট্য বা ভেরিয়েবলের সাথে ভালভাবে কাজ করতে না পারা; শুধুমাত্র দুটি শ্রেণীবিভাগের সমস্যা সমাধান করা যায় (এই ভিত্তিতে প্রাপ্ত সফটম্যাক্স একাধিক শ্রেণিবদ্ধকরণের জন্য ব্যবহার করা যেতে পারে) এবং এটি অবশ্যই লিনিয়ার বিভাজক হতে হবে; অ-রৈখিক বৈশিষ্ট্যগুলির জন্য, রূপান্তর প্রয়োজন;
- ### ৩. লিনিয়ার রিগ্রেশন
লিনিয়ার রিগ্রেশন হল রিগ্রেশনের জন্য, লজিস্টিক রিগ্রেশনের মত নয়, যা শ্রেণিবদ্ধকরণের জন্য ব্যবহৃত হয়। এর মূল ধারণা হল, গ্রেডিয়েন্ট অবনমন পদ্ধতির মাধ্যমে সর্বনিম্ন দ্বিগুণের ফর্মের ত্রুটি ফাংশনকে অপ্টিমাইজ করা। অবশ্যই, এটি স্বাভাবিক সমীকরণ দ্বারা সরাসরি প্যারামিটারের সমাধান পেতে পারে, যার ফলেঃ
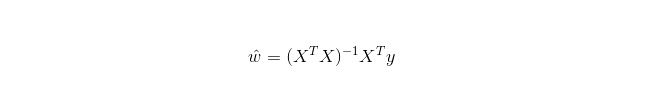
এলডব্লিউএলআর (LWLR) -এর ক্ষেত্রে, পরামিতিটির গণনা করা এক্সপ্রেশন হলঃ
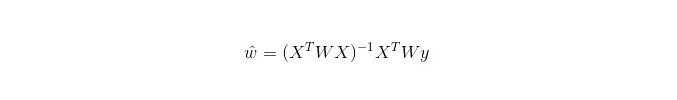
LWLR একটি নন-প্যারামিটার মডেল, কারণ প্রতিবার রিগ্রেশন গণনা করার জন্য প্রশিক্ষণের নমুনাটি কমপক্ষে একবার অতিক্রম করতে হবে।
সুবিধাসমূহঃ সহজ বাস্তবায়ন, সহজ হিসাব;
অসুবিধাঃ অ-রৈখিক তথ্যের সাথে মিলিত হতে পারে না।
- ### ৪. নিকটতম প্রতিবেশী অ্যালগরিদম কেএনএন
কেএনএন হল নিকটতম প্রতিবেশী অ্যালগরিদম, যার প্রধান প্রক্রিয়া হলঃ
প্রশিক্ষণ নমুনা এবং পরীক্ষার নমুনার প্রতিটি নমুনা পয়েন্টের দূরত্ব গণনা করুন (সাধারণ দূরত্বের পরিমাপ ইউরোপীয় দূরত্ব, মার্টিন দূরত্ব ইত্যাদি);
এবং তারপরে, আপনি আপনার দূরত্বের মানটি দেখতে পাবেন।
k টি নমুনার মধ্যে সর্বনিম্ন দূরত্ব নির্বাচন করুন;
এই k টি নমুনার ট্যাগের উপর ভিত্তি করে একটি ভোট দেওয়া হয়, যা চূড়ান্ত শ্রেণিবিন্যাসের জন্য ব্যবহার করা হয়।
কিভাবে একটি সর্বোত্তম K-মান নির্বাচন করা যায় তা ডেটার উপর নির্ভর করে। সাধারণভাবে, শ্রেণিবদ্ধকরণের সময় বৃহত্তর K-মানের ফলে গোলমালের প্রভাব হ্রাস পায়। তবে শ্রেণীর মধ্যে সীমানা অস্পষ্ট হয়ে যায়।
একটি ভাল K-এর মান প্রাপ্ত করা যায় বিভিন্ন প্রতিলিপি প্রযুক্তির মাধ্যমে, যেমন, ক্রস-ভ্যালিডেশন। এছাড়াও, গোলমাল এবং অসংগত বৈশিষ্ট্য ভেক্টরগুলির উপস্থিতি K-এর নিকটবর্তী অ্যালগরিদমের নির্ভুলতা হ্রাস করে।
কাছাকাছি-প্রতিবেশী অ্যালগরিদমের একটি শক্তিশালী সামঞ্জস্যপূর্ণ ফলাফল রয়েছে। তথ্য অসীম হওয়ার সাথে সাথে, অ্যালগরিদমের ত্রুটি হার বেয়েজীয় অ্যালগরিদমের ত্রুটি হারের দ্বিগুণের বেশি হবে না। কিছু ভাল K মানের জন্য, K কাছাকাছি-প্রতিবেশী ত্রুটি হার বেয়েজীয় তত্ত্বগত ত্রুটি হার অতিক্রম করবে না।
কেএনএন অ্যালগরিদমের সুবিধা
তত্ত্বের পরিপক্কতা, সহজ চিন্তাধারা, যা শ্রেণিবদ্ধকরণ বা পুনরাবৃত্তি করার জন্য ব্যবহার করা যেতে পারে; অ-রৈখিক শ্রেণিবিন্যাসের জন্য ব্যবহার করা যেতে পারে; প্রশিক্ষণের সময় জটিলতা হল O (n); তথ্যের উপর কোন অনুমান নেই, উচ্চ নির্ভুলতা এবং বহিরাগতদের প্রতি সংবেদনশীলতা নেই; অভাব
অনেক বেশি গণনা; নমুনা ভারসাম্যহীনতা (অর্থাৎ, কিছু শ্রেণীর নমুনার সংখ্যা বেশি, অন্যদের নমুনার সংখ্যা কম); অনেক বেশি মেমোরির প্রয়োজন।
- ### ৫. সিদ্ধান্ত গাছ
সহজেই ব্যাখ্যা করা যায় ৷ এটি বৈশিষ্ট্যগুলির মধ্যে মিথস্ক্রিয়াগুলিকে চাপমুক্তভাবে পরিচালনা করতে পারে এবং এটি প্যারামিটারহীন, সুতরাং আপনাকে উদ্বেগ করতে হবে না যে অস্বাভাবিক মান বা ডেটাটি লিনিয়ারভাবে পৃথক হতে পারে কিনা ৷ (উদাহরণস্বরূপ, সিদ্ধান্ত গাছটি সহজেই একটি বৈশিষ্ট্য মাত্রা এক্স এর শেষে ক্যাটাগরি এ, মধ্যবর্তী বিভাগে ক্যাটাগরি বি, এবং তারপরে ক্যাটাগরি এ বৈশিষ্ট্য মাত্রা এক্স এর সামনে উপস্থিত হয়) ৷
এর মধ্যে একটি ত্রুটি হল এটি অনলাইন শিক্ষা সমর্থন করে না, তাই নতুন নমুনা আসার পর সিদ্ধান্ত গাছের সম্পূর্ণ পুনর্নির্মাণ প্রয়োজন।
আরেকটি অসুবিধা হল যে এটি খুব সহজেই ওভারফিট হতে পারে, কিন্তু এটি এমন এক সমন্বয় পদ্ধতির প্রবেশদ্বার যেমন র্যান্ডম ফরেস্ট আরএফ (Random Forest RF) বা বুস্টড ট্রি (Boosted Tree) ।
এছাড়াও, র্যান্ডম বন প্রায়শই অনেকগুলি শ্রেণিবদ্ধকরণের সমস্যাগুলির বিজয়ী হয় (সাধারণত ভেক্টর মেশিনের চেয়ে কিছুটা ভাল), এটি দ্রুত এবং সামঞ্জস্যপূর্ণ প্রশিক্ষিত হয়, এবং আপনাকে ভেক্টর মেশিনের মতো অনেকগুলি প্যারামিটার সামঞ্জস্য করার বিষয়ে চিন্তা করতে হবে না, তাই এটি অতীতে জনপ্রিয় ছিল।
সিদ্ধান্ত গাছের একটি গুরুত্বপূর্ণ অংশ হল একটি বৈশিষ্ট্যকে শাখা করার জন্য নির্বাচন করা, তাই তথ্য বৃদ্ধির জন্য গণনা সূত্রটি লক্ষ্য করুন এবং এটি গভীরভাবে বুঝতে চেষ্টা করুন।
ইনফরমেশন বক্সের গণনা সূত্রটি নিম্নরূপঃ
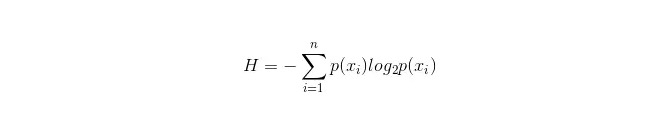
যেখানে n প্রতিনিধিত্ব করে n শ্রেণিবদ্ধকরণ বিভাগ রয়েছে ((যেমন ধরুন এটি একটি 2 শ্রেণীর প্রশ্ন, তাহলে n = 2) । এই 2 শ্রেণীর নমুনার সম্ভাব্যতা p1 এবং p2 গণনা করুন, যা মোট নমুনায় উপস্থিত হয়, যাতে নির্বাচিত বৈশিষ্ট্যগুলির শাখাগুলির আগে তথ্য প্যাকেজ গণনা করা যায়।
এখন একটি অ্যাট্রিবিউট xxi বেছে নিন যা শাখা করার জন্য ব্যবহৃত হবে, এই সময়ে শাখা নিয়মটি হলঃ যদি x = vxi = v হয় তবে নমুনাটি গাছের একটি শাখায় বিভক্ত করা হবে; যদি এটি সমান না হয় তবে অন্য শাখায় প্রবেশ করা হবে।
স্পষ্টতই, শাখাগুলির মধ্যে নমুনা দুটি শ্রেণীর অন্তর্ভুক্ত হওয়ার সম্ভাবনা রয়েছে, এই দুটি শাখাগুলির জন্য H1 এবং H2 গণনা করা হয়, শাখাগুলির পরে মোট তথ্যের জন্য H1 = p1 H1 + p2 H2 গণনা করা হয়, এই মুহুর্তে তথ্য বৃদ্ধি ΔH = H - H2। তথ্য বৃদ্ধি নীতি হিসাবে, সমস্ত বৈশিষ্ট্য একসাথে পরীক্ষা করা হয়, এইবার শাখাগুলির বৈশিষ্ট্য হিসাবে সর্বাধিক বৃদ্ধি প্রাপ্ত একটি বৈশিষ্ট্য বেছে নেওয়া হয়।
সিদ্ধান্তের গাছের সুবিধা
গণনা সহজ, সহজে বোঝা যায় এবং ব্যাখ্যাযোগ্য; অনুপস্থিত বৈশিষ্ট্যযুক্ত নমুনাগুলির তুলনা করা; এটি একটি নতুন পদ্ধতি, যা ব্যবহারকারীদের জন্য একটি নতুন ধারণা তৈরি করে। এই ধরনের তথ্যের জন্য, আপনি একটি বড় ডেটা উত্সের উপর একটি কার্যকর এবং কার্যকর ফলাফল তুলনামূলকভাবে স্বল্প সময়ের মধ্যে তৈরি করতে পারেন। অভাব
(অবৈতনিক বনাঞ্চল ওভারফ্যাটিমেশনের সম্ভাবনা অনেকটাই কমিয়ে দেয়) তথ্যের মধ্যে সম্পর্ককে উপেক্ষা করা; যে সকল শ্রেণীর নমুনার সংখ্যা অসঙ্গতিপূর্ণ, সিদ্ধান্ত গাছের মধ্যে, তথ্য বৃদ্ধির ফলাফলগুলি আরও বেশি সংখ্যক বৈশিষ্ট্যযুক্ত বৈশিষ্ট্যগুলির দিকে ঝুঁকছে (যেমন RF) ।
- ### 5.1 Adaboosting
অ্যাডাবুস্ট একটি সংযোজন মডেল, প্রতিটি মডেল পূর্ববর্তী মডেলের ত্রুটি হারের উপর ভিত্তি করে তৈরি করা হয়, ভুলের নমুনার উপর অতিরিক্ত মনোযোগ দেওয়া হয় এবং সঠিকভাবে শ্রেণিবদ্ধ নমুনার উপর কম মনোযোগ দেওয়া হয়, ধাপে ধাপে পুনরাবৃত্তি করার পরে, একটি তুলনামূলকভাবে ভাল মডেল পাওয়া যায়। এটি একটি আদর্শ বুস্টিং অ্যালগরিদম। নীচে এর সুবিধা এবং অসুবিধাগুলি সংক্ষিপ্ত করা হয়েছে।
সুবিধা
adaboost একটি উচ্চ নির্ভুলতা শ্রেণিবিন্যাসকারী। বিভিন্ন পদ্ধতি ব্যবহার করে একটি উপশ্রেণীকরণ তৈরি করা যেতে পারে। Adaboost অ্যালগরিদম একটি কাঠামো প্রদান করে। সহজ শ্রেণিবিন্যাসক ব্যবহার করার সময়, গণনা করা ফলাফলগুলি বোঝা যায় এবং দুর্বল শ্রেণিবিন্যাসকের গঠন অত্যন্ত সহজ। এটি সহজ, বৈশিষ্ট্য বাছাইয়ের প্রয়োজন নেই। ওভারফিটিংয়ের সম্ভাবনা কম। র্যান্ডম ফরেস্ট এবং GBDT এর মতো সমন্বয় অ্যালগরিদম সম্পর্কে, এই নিবন্ধটি দেখুনঃ মেশিন লার্নিং - সমন্বয় অ্যালগরিদমের সংক্ষিপ্তসার
অসুবিধাঃ আউটলিয়ারের প্রতি সংবেদনশীল
- ### ৬. এসভিএম ভেক্টর মেশিন সমর্থন করে
উচ্চ নির্ভুলতা ওভারফিট এড়ানোর জন্য একটি ভাল তাত্ত্বিক গ্যারান্টি প্রদান করে, এবং এটি একটি উপযুক্ত কোর ফাংশন দিয়ে ভাল কাজ করে, এমনকি যদি ডেটা মূল বৈশিষ্ট্য স্পেসে লিনিয়ারভাবে অবিচ্ছেদ্য হয়।
অ্যানিমেটেড ফরেস্ট (অ্যানিমেটেড ফরেস্ট) বিশেষ করে উচ্চ মাত্রার টেক্সট শ্রেণিবিন্যাস সমস্যার ক্ষেত্রে বেশ জনপ্রিয়। দুর্ভাগ্যবশত, এটি মেমরি খরচ করে, ব্যাখ্যা করা কঠিন, এবং এটি চালানো এবং প্যারামিটারিংয়ের জন্য কিছুটা বিরক্তিকর, যখন র্যান্ডম ফরেস্ট এই ত্রুটিগুলি এড়িয়ে চলে এবং তুলনামূলকভাবে কার্যকর।
সুবিধা এটি একটি উচ্চ মাত্রার সমস্যা সমাধান করে, যা একটি বড় বৈশিষ্ট্যযুক্ত স্থান। অ-রৈখিক বৈশিষ্ট্যগুলির সাথে ইন্টারঅ্যাকশন পরিচালনা করতে সক্ষম; এই তথ্যের উপর নির্ভর না করে; এটি আমাদেরকে আরও শক্তিশালী করে তোলে।
অভাব “অনেক নমুনা পর্যবেক্ষণের ফলে কার্যকারিতা খুব বেশি হয় না। অ-রৈখিক সমস্যার কোন সার্বজনীন সমাধান নেই, এবং মাঝে মাঝে একটি উপযুক্ত কোর ফাংশন খুঁজে পাওয়া কঠিন; তথ্যের অভাবের প্রতি সংবেদনশীলতা; কার্নের ক্ষেত্রেও চ্যালেঞ্জিং (libsvm-এ চারটি কার্নিয়াল ফাংশন রয়েছেঃ লিনিয়ার কার্নিয়াল, মাল্টিপল কার্নিয়াল, আরবিএফ এবং সিগময়েড কার্নিয়াল):
প্রথমত, যদি নমুনার সংখ্যা বৈশিষ্ট্য সংখ্যার চেয়ে কম হয়, তাহলে অ-রৈখিক কোর বেছে নেওয়ার দরকার নেই, কেবলমাত্র রৈখিক কোর ব্যবহার করা যেতে পারে;
দ্বিতীয়ত, যদি নমুনার সংখ্যা বৈশিষ্ট্যের সংখ্যার চেয়ে বেশি হয়, তাহলে নমুনাকে উচ্চতর মাত্রায় ম্যাপ করার জন্য অ-রৈখিক কোর ব্যবহার করা যেতে পারে, যা সাধারণত আরও ভাল ফলাফল দেয়।
তৃতীয়ত, যদি নমুনার সংখ্যা এবং বৈশিষ্ট্যের সংখ্যা সমান হয়, তবে এই ক্ষেত্রে অ-রৈখিক কোর ব্যবহার করা যেতে পারে, নীতিটি দ্বিতীয়টির মতোই।
প্রথম ক্ষেত্রে, আপনি প্রথমে ডেটা হ্রাস করতে পারেন এবং তারপরে নন-লাইনিয়ার কোর ব্যবহার করতে পারেন, এটিও একটি পদ্ধতি।
- ### ৭. কৃত্রিম নিউরাল নেটওয়ার্কের সুবিধা ও অসুবিধা
এফএনএন এর সুবিধাগুলোঃ শ্রেণিবিন্যাসের উচ্চ নির্ভুলতা; এটি একটি শক্তিশালী সমান্তরাল বিতরণ প্রসেসিং, বিতরণ স্টোরেজ এবং শেখার ক্ষমতা। নয়েজ স্নায়ুর জন্য শক্তিশালী রুক্ষতা এবং ত্রুটি-সহনশীলতা, যা জটিল অ-রৈখিক সম্পর্কের জন্য যথেষ্ট; এটি একটি স্মৃতিশক্তির সাথে যুক্ত।
এপিএন এর অসুবিধাঃ নিউরাল নেটওয়ার্কের জন্য প্রচুর পরিমাণে প্যারামিটার প্রয়োজন, যেমন নেটওয়ার্ক টপোগ্রাফিকাল কাঠামো, প্রাথমিক মান এবং থ্রেশহোল্ড। যেহেতু শিক্ষার প্রক্রিয়া পর্যবেক্ষণের মধ্যে সীমাবদ্ধ, তাই ফলাফলের বিশ্বাসযোগ্যতা এবং গ্রহণযোগ্যতাকে প্রভাবিত করে এমন ফলাফলের ব্যাখ্যা করা কঠিন; আপনি আপনার লক্ষ্যে পৌঁছতে না পেরেও পড়তে পারেন।
- ### ৮, কে-মিস ক্লাস্টার
K-Means ক্লাস্টার সম্পর্কে আগে একটি নিবন্ধ লিখেছি। এটি একটি মেশিন লার্নিং অ্যালগরিদম- K-means ক্লাস্টার।
সুবিধা অ্যালগরিদম সহজ এবং বাস্তবায়ন করা সহজ; বড় ডেটাসেটগুলির সাথে কাজ করার জন্য, এই অ্যালগরিদমটি তুলনামূলকভাবে স্কেলযোগ্য এবং দক্ষ, কারণ এর জটিলতা প্রায় O ((nkt) হয়, যেখানে n হল সমস্ত বস্তুর সংখ্যা, k হল ক্রমের সংখ্যা, এবং t হল পুনরাবৃত্তির সংখ্যা। সাধারণত k < < n। এই অ্যালগরিদমটি সাধারণত স্থানীয়ভাবে সংযুক্ত হয়। < p=”“> অ্যালগরিদমটি এমন k টি বিভাজন খুঁজে বের করার চেষ্টা করে যা বর্গক্ষেত্রের ত্রুটি ফাংশনের মানকে সর্বনিম্ন করে দেয়। যখন সিলিন্ডারগুলি ঘন, গোলাকার বা কুণ্ডলীযুক্ত হয় এবং সিলিন্ডার এবং সিলিন্ডারগুলির মধ্যে পার্থক্য স্পষ্ট হয়, তখন ক্লাস্টারিংয়ের প্রভাব ভাল হয়।
অভাব সংখ্যাসূচক ডেটার জন্য ডেটা টাইপের উচ্চতর প্রয়োজনীয়তা; স্থানীয় ন্যূনতম সংযোজন হতে পারে, বড় আকারের ডেটাতে সংযোজন ধীর K এর মান নির্বাচন করা কঠিন; প্রাথমিক মানের কেন্দ্রীয় মান সংবেদনশীল, যা বিভিন্ন প্রাথমিক মানের জন্য বিভিন্ন ক্লাস্টারিং ফলাফলের দিকে পরিচালিত করতে পারে; এটি এমন একটি পাত্রের জন্য উপযুক্ত নয় যেটি একটি অ-উল্লেখযোগ্য আকৃতির পাত্র বা আকারের একটি বড় পার্থক্য খুঁজে পায়। অল্প পরিমাণে এই ধরনের ডেটা গড়ের উপর ব্যাপক প্রভাব ফেলতে পারে।
আলগোরিদিম নির্বাচন রেফারেন্স
এর আগে আমি বিদেশে কিছু নিবন্ধ অনুবাদ করেছি এবং একটি নিবন্ধে একটি সহজ অ্যালগরিদম নির্বাচন কৌশল দেওয়া হয়েছেঃ
প্রথমত, লজিক্যাল রিগ্রেশন বেছে নেওয়া উচিত, যদি এর কার্যকারিতা খুব ভাল না হয়, তবে এর ফলাফলগুলি একটি বেঞ্চমার্ক হিসাবে উল্লেখ করা যেতে পারে, যা অন্য অ্যালগরিদমের সাথে তুলনা করা যেতে পারে;
তারপর সিদ্ধান্ত গাছ (random forest) পরীক্ষা করে দেখুন আপনার মডেলের পারফরম্যান্সকে অনেকটা উন্নত করা যায় কিনা। এমনকি যদি আপনি এটিকে আপনার চূড়ান্ত মডেল হিসেবে না বিবেচনা করেন, আপনি র্যান্ডম বন ব্যবহার করে শব্দ পরিবর্তনশীল অপসারণ করতে পারেন এবং বৈশিষ্ট্য নির্বাচন করতে পারেন।
যদি বৈশিষ্ট্যগুলির সংখ্যা এবং পর্যবেক্ষণের নমুনাগুলি বিশেষভাবে বেশি হয়, তবে যখন পর্যাপ্ত সংস্থান এবং সময় থাকে (এটি গুরুত্বপূর্ণ), এসভিএম ব্যবহার করা একটি বিকল্প।
সাধারণতঃ GBDT>=SVM>=RF>=Adaboost>=Other…, এখন গভীরতা শেখার খুব জনপ্রিয়, অনেক ক্ষেত্রেই ব্যবহৃত হয়, এটি নিউরাল নেটওয়ার্কের উপর ভিত্তি করে, বর্তমানে আমি নিজেও শিখছি, কেবল তাত্ত্বিক জ্ঞান খুব ঘন নয়, বোঝার জন্য যথেষ্ট গভীর নয়, এখানে পরিচয় করিয়ে দেওয়া হবে না।
অ্যালগরিদম গুরুত্বপূর্ণ, কিন্তু ভাল ডেটা ভাল অ্যালগরিদমের চেয়ে ভাল, এবং ভাল ডিজাইনের বৈশিষ্ট্যগুলি উপকারী। যদি আপনার কাছে একটি বিশাল ডেটা সেট থাকে তবে আপনি যে অ্যালগরিদম ব্যবহার করেন তা শ্রেণিবদ্ধকরণের কার্যকারিতার উপর খুব বেশি প্রভাব ফেলতে পারে না (এই মুহুর্তে আপনি গতি এবং ব্যবহারের সহজতার ভিত্তিতে সিদ্ধান্ত নিতে পারেন) ।
-
তথ্যসূত্র