ঝুঁকিপূর্ণ ছোট স্টিফেন (৪) মোভার এবং দেবতার বক্ররেখা

গত সংখ্যায় বলা হয়েছিল যে, জ্যাকব বার্নুলি মৃত্যুর সময় তার সম্ভাব্যতা তত্ত্বের বইয়ের অনুমানমূলক তত্ত্ব প্রকাশিত হয়নি। তার পাণ্ডুলিপিগুলি সংকলনের কাজটি তার চাচাতো ভাই নিকোলাস দ্বিতীয় বার্নুলির হাতে দেওয়া হয়েছিল (এটি ছিল সেই প্রাতঃরাশের প্রতিভা) । চাচার ইচ্ছার পরে নিকোলাস সত্যিকারের সম্ভাব্যতার বিপরীতে বিচ্যুতির স্তরটি পরীক্ষা করতে শুরু করেছিলেন। সম্ভবত প্রতিভাধররাও ধ্যান-ধ্যানের মধ্যে নিজেকে নিরুৎসাহিত বোধ করেছিলেন, তাই ডন মর্ফকে গবেষণায় যোগদানের জন্য আমন্ত্রণ জানিয়েছিলেন। মোইভর (Abraham de Moivre) অনেক জায়গায় মেভর হিসেবে অনুবাদ করা হয়, কিন্তু তার প্রতিকৃতি দেখে আমি এই অনুবাদটির পক্ষে নই। এই আমন্ত্রণটি পরকালের জন্য একটি প্রশংসিত সংখ্যা (ji) তত্ত্ব (you) জগতে একটি চমৎকার বক্তব্য অর্জন করতে পারে, কিন্তু মোইভর তা প্রত্যাখ্যান করেছিলেন। এবং তিনি এই কারণেই প্রত্যাখ্যান করেছিলেন যে তিনি অনুভব করেছিলেন যে তিনি যথেষ্ট শক্তিশালী নন।

• ডেমোফার জ্যাকব বার্নুলির থেকে মাত্র এক বছর ছোট, এবং তার পুরো জীবনকে একটি উপন্যাসের আওতায় আনা যায়, দ্য ম্যারিটরিয়াল ওয়ার্ল্ড ওয়ার্ল্ড ওয়ার্ল্ড ওয়ার্ল্ড ওয়ার্ল্ড ওয়ার্ল্ড। ফ্রান্স তখন একটি ক্যাথলিক দেশ ছিল, এবং দ্য মর্ফ সম্ভবত একজন প্রোটেস্ট্যান্ট ছিলেন। পরে, ফ্রান্সের রাজা লুই চতুর্দশ একটি আইন জারি করে ঘোষণা করেছিলেন যে দেশটির প্রোটেস্ট্যান্টরা নিম্নমানের নাগরিক এবং শিশুদের অবশ্যই প্রোটেস্ট্যান্ট ধর্মে রূপান্তরিত করতে হবে। এই পদ্ধতিটি মূলত ফ্রান্সে প্রোটেস্ট্যান্টকে একটি ধর্মীয় ধর্মীয় সম্প্রদায় হিসাবে চিহ্নিত করেছিল, এবং দ্য মর্ফ এর জন্য দু’বছর জেল খাটানো হয়েছিল। কারাগার থেকে বেরিয়ে আসা দ্য মর্ফ ইংল্যান্ডে পালিয়ে যাওয়ার চেষ্টা করেছিল, তবে তিনি একাডেমিক জগতে কোনও পদ পাননি, যদিও তিনি নিউটনের বন্ধু ছিলেন এবং ৩০ বছর বয়সে তিনি ব্রিটিশ রাজপরিবারের সদস্য ছিলেন।

কিন্তু আমরা এখানে চিৎকার করে বলতে চাই যে, বেন মর্ফ চিরকাল বেঁচে থাকুক! ১৭১১ সালে বেন মর্ফ একটি বই প্রকাশ করেন যা ভাগ্যকে পরিমাপ করার জন্য ব্যবহৃত হয়, এবং যদি সেই সময়ে কোন বইয়ের কভার থাকত, তবে নিউটনের পরামর্শটি অবশ্যই কভারে লেখা হতঃ বেন মর্ফকে জিজ্ঞাসা করুন, তিনি এই বিষয়ে আমার চেয়ে বেশি জানেন।

কিন্তু সেই সময়ে তা ছিল না, তাই ডন মোভরও খুব বেশি ট্যাক্স নিতে পারেননি।

আপনি হয়তো মনে রাখবেন যে, আমাদের আগের প্রশ্নের (ঝুঁকিপূর্ণ গল্প (৩): কমরেড বার্নুলি) উত্তরটি হল, একটি বাক্সের মধ্যে ৫,০০০ টুকরো পাথরের জন্য, আমরা মোট পাথরের অনুপাত অনুমান করতে ২৫,৫০০ বার ধরে ফেলতে পারি। কিন্তু আপনি হয়তো দেখতে পাবেন যে, ২৫,৫০০ বার ধরে ফেলা অনেক বেশি, বরং পাথরটি এক এক করে ফেলে দেওয়া ভালো।

মোফর বিমূর্ততা এবং পাস্কার ত্রিভুজ পদ্ধতি ব্যবহার করে একটি গ্রুপিং স্যাম্পলিং পদ্ধতি অবলম্বন করেছেন। তিনি ধরে নিয়েছেন যে, প্রতিবার 100 টি গোলাকার পাথর বের করে, কালো এবং সাদা গোলাকার পাথরগুলির অনুপাত রেকর্ড করে এবং তারপরে পাথরগুলি আবার ফিরিয়ে দেয়, এবং একইভাবে পুনরায় স্যাম্পলিং করে। এই পদ্ধতির মাধ্যমে, মোফর আপনাকে আপনার রেকর্ড করা অনুপাতের প্রকৃত অনুপাতের কাছাকাছি বিচ্যুতি এবং কীভাবে এই অনুপাতগুলি তাদের গড়ের চারপাশে বিতরণ করা হয়েছে তা আপনাকে আগেই বলতে পারে।

এই কথাটি কি আপনার কাছে পরিচিত মনে হচ্ছে, নাকি আপনার কাছেই আছে, অথবা আপনি কি তাৎক্ষণিকভাবে এটির নাম বলতে চান? হ্যাঁ, এটি হ’ল সাধারণ সাধারণ বন্টন। সাধারণ সাধারণ বন্টনের কার্ভটি একটি ঘন্টাধ্বনিযুক্ত কার্ভের মতো, বেশিরভাগ পর্যবেক্ষণের মানগুলি মাঝখানে, সমস্ত পর্যবেক্ষণের গড়ের কাছাকাছি, এবং তারপরে সমান্তরাল থেকে সমান্তরালভাবে উভয় প্রান্তে ঝাঁকুনি দেওয়া হয়, এবং গড়ের উভয় প্রান্তের পর্যবেক্ষণের সংখ্যা সমান। শুরুতে কার্ভটি দ্রুত গতির নিচে ঝাঁকুনিযুক্ত ছিল, এবং উভয় প্রান্তে, এই প্রান্তটি সমতল হয়ে যায়, যার অর্থ হল যে পরিমাণ পর্যবেক্ষণের মানগুলি গড় থেকে দূরে থাকে তার সম্ভাবনা কম। অনেক বছর পরে, যে কোনও পরিসংখ্যানের পাঠ্যপুস্তকে এই কার্ভের একটি বিবরণ রয়েছে এবং এটিকে বলা হয় মর্ফিয়াল সীমাবদ্ধতার কেন্দ্র।

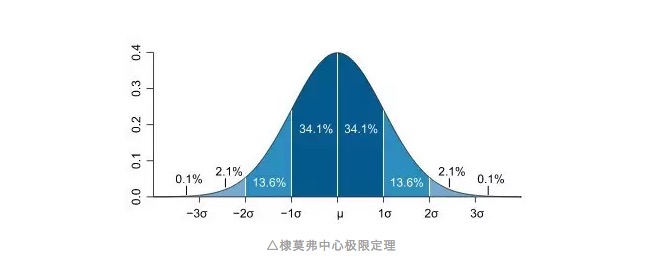
এইভাবে আমরা স্ট্যান্ডার্ড ডিভার্জেন্সের ধারণাটি প্রবর্তন করতে পারি, যা আমরা জনসাধারণের অন্যান্য নিবন্ধে উল্লেখ করেছি। স্ট্যান্ডার্ড ডিভার্জেন্সটি মূলত পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপ করে, বা আমরা এটিকে পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমাপের পরিমা

একজন ধার্মিক ধর্মাবলম্বী হিসাবে, ডনমোভার মনে করেন যে ঘন্টাধ্বনিযুক্ত বক্ররেখাটি ঈশ্বরের সৃষ্টি। তাঁর মতে, এই ধরনের পরিমাপের মাধ্যমে আমরা অনিশ্চয়তাকে পরাস্ত করতে পারি এবং তারপরে সমস্ত ঝুঁকিকে জয় করতে পারি, কারণ বক্ররেখায় সমস্ত সম্ভাব্য ঘটনা এবং তাদের সম্ভাব্যতা বর্ণনা করা হয়েছে, সম্ভবত দুর্ঘটনাজনিত কারণে তথাকথিত বিচ্যুতি ঘটবে, তবে সময়ের সাথে সাথে এই বিচ্যুতিগুলি আমাদের সংক্ষিপ্ত আইনকে প্রভাবিত করবে না।

আমরা সবাই খুব খুশি হয়েছি যে, আমাদের হতাশার কারণ হল যে আমরা মাঝে মাঝে ফোন নম্বর ডায়াল করতে পারি না, তাই আমরা বারবার চেষ্টা করি, কিন্তু আমরা উত্তর পাই না। উচ্চ মাধ্যমিক বিদ্যালয়ের একটি ক্লাসিক বিষয় (আরে, আমি কেন উচ্চ মাধ্যমিক বিদ্যালয়ের বিষয় ব্যবহার করি) হল পণ্যের উত্তীর্ণতার হার। যদি একটি পণ্যের জন্য, শিল্পের মানদণ্ড বলে যে বর্জ্যের হার 0.1% এর বেশি নয়, তবে এটি উত্তীর্ণ হওয়ার অর্থ হল আমরা 10,000 টি পণ্য বেছে নিয়েছি, যার মধ্যে যদি 10 টির বেশি বর্জ্য না থাকে তবে এটি উত্তীর্ণ হয়েছে। কিন্তু ফলাফলটি হল যে 10,000 টির মধ্যে 12 টি অবশেষে উপস্থিত হয়, যদি পণ্যের বর্জ্যের হার 0.1% হয় তবে আমরা আসলে আমাদের 12 টি বর্জ্যের সম্ভাবনা গণনা করার জন্য বেনমোর পদ্ধতি ব্যবহার করতে পারি।

কিন্তু এই প্রশ্নটি আমাদের কাছে প্রায়শই অর্থহীন। কারণ আমরা হয়তো জানি না যে পণ্যের গড় বর্জ্যের হার কত হবে, এবং যদি গড় বর্জ্যের হার পরীক্ষার মানের চেয়ে বেশি হয়, তাহলে আমাদের পণ্যগুলির একটি ব্যাচ পরীক্ষার মধ্য দিয়ে যাওয়ার সম্ভাবনা কত? যদি 20,000 পণ্য পরীক্ষা করা হয়, তাহলে 10,000 পণ্যের ফলাফল সরাসরি ব্যবহার করা যেতে পারে? এই প্রশ্নগুলি পনমোরের বক্ররেখা দিয়ে ব্যাখ্যা করা খুব বেশি ঝামেলা বলে মনে হচ্ছে। সুতরাং, একটি বেয়েস এর নামটি সমস্ত পরিসংখ্যানবিদ্যা এবং পনমোরোসিস পাঠ্যপুস্তকে উপস্থিত হবে, এবং এটি আমাদের পরবর্তী সংস্করণে থাকবে।

চীনের কোয়ান্টাম ইনভেস্টমেন্ট অ্যাসোসিয়েশনের সৌজন্যে