Backtesting einer Intraday Mean Reverssion Pairs Strategie zwischen SPY und IWM

In diesem Artikel werden wir unsere erste Intraday-Handelsstrategie betrachten. Es wird eine klassische Handelsidee, die von Handelspaaren, verwendet. In diesem Fall werden wir zwei Exchange Traded Funds (ETFs), SPY und IWM, verwenden, die an der New York Stock Exchange (NYSE) gehandelt werden und versuchen, die US-Börsenindizes, den S&P500 und den Russell 2000, zu repräsentieren.

Die Strategie erzeugt im Großen und Ganzen einen Spread zwischen dem ETF-Paar, indem man den einen Longing und den anderen Shorting vornimmt. Das Verhältnis von Long zu Short kann auf viele Arten definiert werden, z. B. durch Verwendung statistischer Cointegrationszeitreihen. In diesem Szenario werden wir ein Hedge-Verhältnis zwischen SPY und IWM über eine rollende lineare Regression berechnen. Dies ermöglicht es uns dann, einen Spread zwischen SPY und IWM zu erstellen, der auf einen z-Score normalisiert wird. Die Handelssignale werden generiert, wenn der z-Score bestimmte Schwellenwerte überschreitet, unter der Überzeugung, dass der Spread zum Mittel zurückkehrt.

Der Grund für die Strategie ist, dass SPY und IWM ungefähr die gleiche Situation charakterisieren, die der Wirtschaft einer Gruppe von US-Unternehmen mit hoher und geringer Kapitalkapitalisierung. Die Prämisse ist, dass, wenn man den Preisspread annimmt, dann der Durchschnittswert umgekehrt werden sollte, da, während lokale (zeitliche) Ereignisse entweder den S&P500 oder den Russell 2000-Index separat beeinflussen können (z. B. Differenzen zwischen kleinen und großen Kapitalkapitalisierungen, Re-Balancing-Daten oder Blocktrades), die langfristigen Preisreihen der beiden wahrscheinlich miteinander integriert werden.

Die Strategie

Die Strategie wird in folgenden Schritten durchgeführt:

1. Die Daten - 1-minütige Balken von SPY und IWM werden von April 2007 bis Februar 2014 gewonnen.
2. Verarbeitung - Die Daten sind korrekt ausgerichtet und fehlende Balken werden gegenseitig verworfen.
3. Spread - Die Absicherungsquote zwischen den beiden ETFs wird durch eine rollende lineare Regression berechnet. Dies wird als der β-Regressionskoeffizient definiert, der ein Rückblickfenster verwendet, das um 1 Bar nach vorne verschiebt und die Regressionskoeffizienten neu berechnet. So wird die Absicherungsquote βi für bar bi über die Punkte bi−1−k bis bi−1 für einen Rückblick von k Bars berechnet.
4. Z-Score - Der Standard-Score des Spreads wird in der üblichen Weise berechnet. Dies bedeutet, den (Stichproben-) Mittelwert des Spreads abzuziehen und durch die (Stichproben-) Standardabweichung des Spreads zu dividieren. Der Grund dafür ist, Schwellenparameter einfacher zu interpretieren, da der Z-Score eine dimensionlose Größe ist. Ich habe absichtlich eine Lookahead-Voreingenommenheit in die Berechnungen eingeführt, um zu zeigen, wie subtil es sein kann. Versuchen Sie und achten Sie darauf!
5. Trades - Lange Signale werden erzeugt, wenn der negative Z-Score unter eine vorgegebene (oder nachoptimierte) Schwelle fällt, während kurze Signale umgekehrt sind. Ausgangssignale werden erzeugt, wenn der absolute Z-Score unter eine zusätzliche Schwelle fällt. Für diese Strategie habe ich (etwas willkürlich) eine absolute Eintrittsschwelle von ┃z ┃z = 2 und eine Austrittsschwelle von ┃z ┃z ┃z = 1 gewählt.

Der nächste Abschnitt beschreibt einen vollständigen Python-Code (Single-File) zur Implementierung dieser Mean-Reverting-Strategie.

Implementierung von Python

Wie bei allen Python/Pandas-Tutorials ist es notwendig, eine Python-Forschungsumgebung wie in diesem Tutorial beschrieben einzurichten.

Die spezifischen Bibliotheksversionen, die ich benutze, sind wie folgt:

• Python - 2.7.3
• NumPy - 1.8.0
• Pandas - 0.12.0
• Matplotlib - 1.1.0 Lasst uns die Bibliotheken importieren:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Die folgende Funktion create_pairs_dataframe importiert zwei CSV-Dateien, die die Intraday-Bars von zwei Symbolen enthalten. In unserem Fall werden dies SPY und IWM sein. Es erstellt dann ein separates Dataframe-Paar, das die Indizes beider Originaldateien verwendet. Da ihre Zeitstempel aufgrund von verpassten Trades und Fehlern wahrscheinlich unterschiedlich sind, garantiert dies, dass wir passende Daten haben. Dies ist einer der Hauptvorteile der Verwendung einer Datenanalyse-Bibliothek wie Pandas. Der boilerplate-Code wird für uns sehr effizient verarbeitet.

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Der nächste Schritt besteht darin, die rollende lineare Regression zwischen SPY und IWM durchzuführen. In diesem Fall ist IWM der Prädiktor (x) und SPY ist die Antwort (y). Ich habe ein Standard-Lookback-Fenster von 100 Balken festgelegt. Wie oben beschrieben, ist dies ein Parameter der Strategie. Damit die Strategie als robust angesehen wird, möchten wir im Idealfall ein Renditeprofil (oder ein anderes Leistungsmaß) als konvexe Funktion der Lookback-Periode sehen.

Sobald der rollende Beta-Koeffizient im linearen Regressionsmodell für SPY-IWM berechnet wurde, fügen wir ihn den Paaren DataFrame hinzu und lassen die leeren Zeilen fallen. Dies bildet den ersten Satz von Balken, der der Größe des Lookbacks als Trimmmaß entspricht. Wir erstellen dann die Ausbreitung der beiden ETFs als Einheit von SPY und −βi Einheiten von IWM. Offensichtlich ist dies keine realistische Situation, da wir Bruchteile von IWM nehmen, was in einer realen Implementierung nicht möglich ist.

Schließlich erstellen wir den Z-Score des Spreads, der berechnet wird, indem wir den Mittelwert des Spreads subtrahieren und durch die Standardabweichung des Spreads normalisieren. Beachten Sie, dass hier eine ziemlich subtile Lookahead-Voreingenommenheit auftritt. Ich habe es absichtlich im Code gelassen, weil ich betonen wollte, wie einfach es ist, einen solchen Fehler in der Forschung zu machen. Der Mittelwert und die Standardabweichung werden für die gesamte Spread-Zeitserie berechnet. Wenn dies eine wahre historische Genauigkeit widerspiegelt, dann wären diese Informationen nicht verfügbar gewesen, da sie implizit zukünftige Informationen verwenden. Daher sollten wir einen rollenden Mittelwert und stdev verwenden, um den Z-Score zu berechnen.

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

In create_long_short_market_signals werden die Handelssignale erstellt. Diese werden berechnet, indem man den Spread lang geht, wenn der z-Score einen negativen z-Score negativ übersteigt, und den Spread kurz geht, wenn der z-Score einen positiven z-Score positiv übersteigt. Das Exit-Signal wird gegeben, wenn der absolute Wert des z-Score kleiner oder gleich einer anderen (kleinen Größenordnung) Schwelle ist.

Um diese Situation zu erreichen, ist es notwendig zu wissen, ob die Strategie für jeden Balken in oder out des Marktes ist. long_market und short_market sind zwei Variablen, die definiert werden, um die langen und kurzen Marktpositionen zu verfolgen. Leider ist dies viel einfacher, iterativ zu programmieren als ein vektorisierter Ansatz und somit ist es langsam zu berechnen. Trotz 1-minütiger Balken, die ~ 700.000 Datenpunkte pro CSV-Datei erfordern, ist es immer noch relativ schnell zu berechnen auf meiner älteren Desktop-Maschine!

Um über einen Panda DataFrame zu iterieren (was zugegebenermaßen KEINE übliche Operation ist), ist es notwendig, die Iterrows-Methode zu verwenden, die einen Generator zur Verfügung stellt, über den man iterieren kann:

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

In diesem Stadium haben wir Paare aktualisiert, um die tatsächlichen Long/Short-Signale zu enthalten, wodurch wir feststellen können, ob wir auf dem Markt sein müssen. Jetzt müssen wir ein Portfolio erstellen, um den Marktwert der Positionen zu verfolgen. Die erste Aufgabe besteht darin, eine Positionsspalte zu erstellen, die die langen und kurzen Signale kombiniert. Dies enthält eine Liste von Elementen von (1,0,−1), wobei 1 eine Long/Marktposition darstellt, 0 keine Position (ausgegangen werden sollte) und -1 eine Short/Marktposition darstellt. Die Sym1 und Sym2 Spalten stellen die Marktwerte der SPY- und IWM-Positionen am Ende jedes Balkens dar.

Sobald die ETF-Marktwerte erstellt wurden, summieren wir sie, um am Ende jedes Balkens einen Gesamtmarktwert zu erzeugen. Dies wird dann durch die pct_change-Methode für dieses Serieobjekt in einen Renditefluss umgewandelt. Nachfolgende Codezeilen klären die schlechten Einträge (NaN- und inf-Elemente) und berechnen schließlich die volle Eigenkapitalkurve.

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

DieHauptDie intraday CSV-Dateien befinden sich auf dem Datadir-Pfad.

Um festzustellen, wie empfindlich die Strategie für die Lookback-Periode ist, ist es notwendig, eine Leistungsmetrik für eine Reihe von Lookbacks zu berechnen. Ich habe die endgültige Gesamtprozentsatzrendite des Portfolios als Leistungsmaßnahme und den Lookback-Bereich in [50,200] mit Schritten von 10 ausgewählt.

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

Das Diagramm der Lookback-Periode gegenüber den Renditen kann nun gesehen werden. Beachten Sie, dass es ein 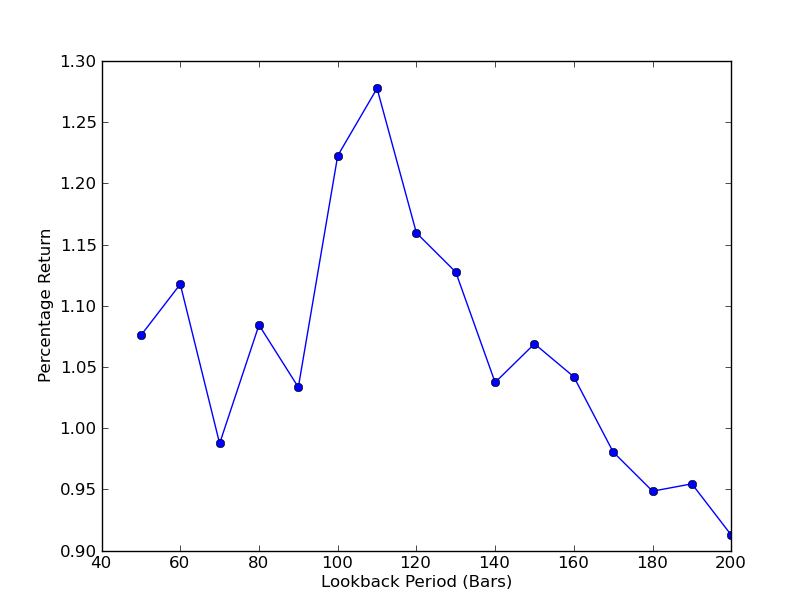global Maximum um einen Lookback gibt, das 110 Balken entspricht. Wenn wir eine Situation gesehen hätten, in der Lookback unabhängig von Renditen war, wäre dies Anlass zur Sorge gewesen:SPY-IWM-Linearregressions-Hedge-Ratio Rückblick-Periodenempfindlichkeitsanalyse

Ein Backtesting-Artikel wäre ohne eine nach oben geneigte Eigenkapitalkurve nicht vollständig! Wenn Sie also eine Kurve der kumulierten Renditen gegenüber der Zeit zeichnen möchten, können Sie den folgenden Code verwenden. Es wird das aus der Lookback-Parameterstudie generierte Endportfolio zeichnen. Daher ist es notwendig, den Lookback zu wählen, je nachdem, welches Chart Sie visualisieren möchten. Das Chart zeichnet auch die Renditen von SPY in demselben Zeitraum aus, um den Vergleich zu erleichtern:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

Die folgende Aktienkurve zeigt einen Rückblick auf einen Zeitraum von 100 Tagen: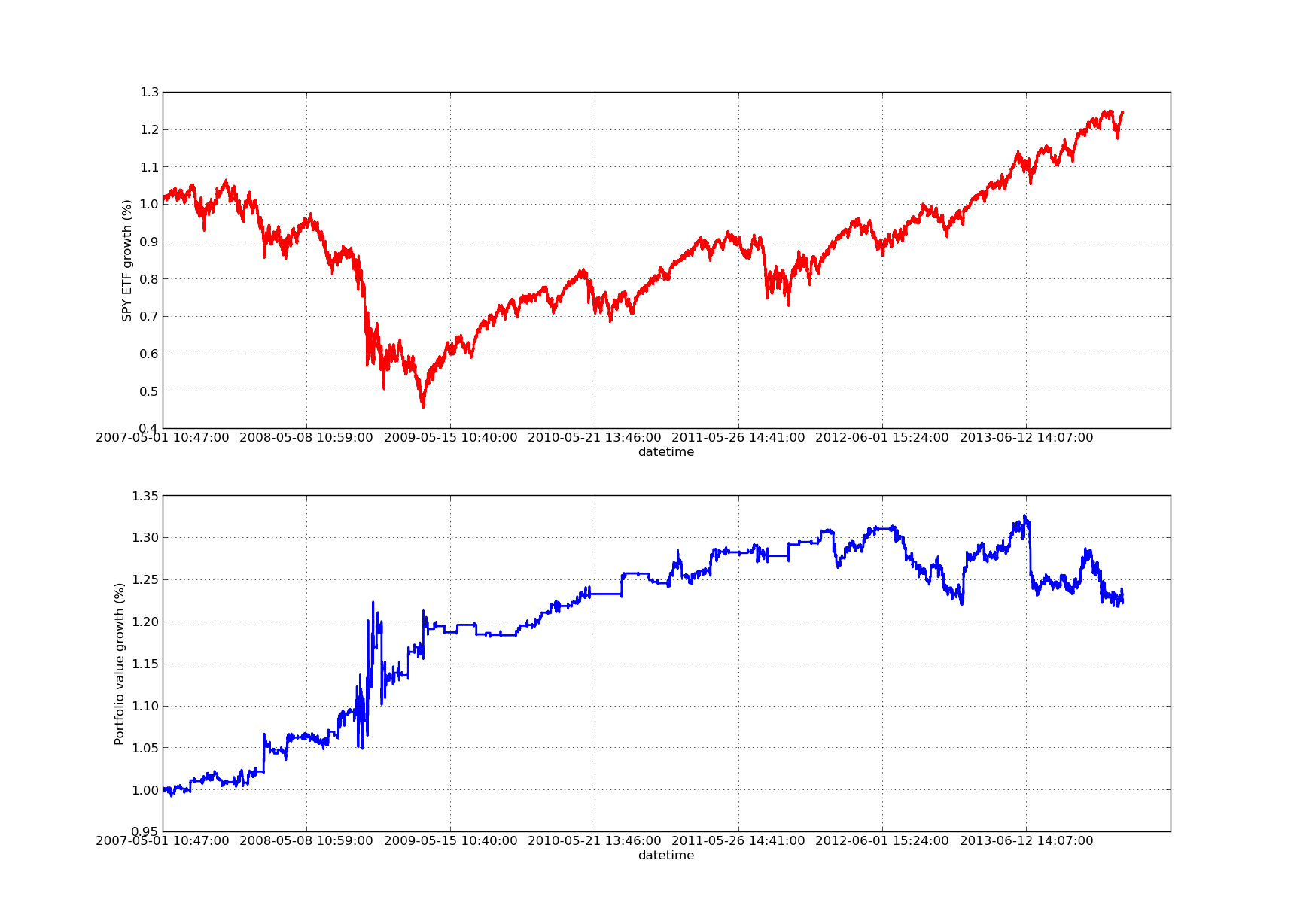SPY-IWM-Linearregressions-Hedge-Ratio Rückblick-Periodenempfindlichkeitsanalyse

Es sei darauf hingewiesen, dass der Rückzug von SPY im Jahr 2009 während der Finanzkrise erheblich war. Die Strategie hatte in diesem Stadium auch eine volatile Periode. Es sei auch darauf hingewiesen, dass sich die Performance im letzten Jahr aufgrund der stark tendenziellen Natur von SPY in diesem Zeitraum, der den S&P500-Index widerspiegelt, etwas verschlechtert hat.

Beachten Sie, dass wir bei der Berechnung des Z-Scores des Spreads immer noch die Lookahead-Voreingenommenheit berücksichtigen müssen. Darüber hinaus wurden alle diese Berechnungen ohne Transaktionskosten durchgeführt. Diese Strategie würde sicherlich sehr schlecht abschneiden, sobald diese Faktoren berücksichtigt werden. Gebühren, Bid/Ask-Spread und Slippage werden derzeit nicht berücksichtigt. Darüber hinaus handelt die Strategie in Bruchteilen von ETFs, was auch sehr unrealistisch ist.

In späteren Artikeln werden wir einen viel komplexeren ereignisgesteuerten Backtester erstellen, der diese Faktoren berücksichtigt und uns deutlich mehr Vertrauen in unsere Eigenkapitalkurve und Leistungsmetriken gibt.