Können Sie Gorillas entkommen, indem Sie mit SVM-Vektormaschinen wetten (handeln)?

Meine Damen und Herren, setzen Sie Ihre Einsätze. Heute werden wir alles tun, um einen Orang-Unsch zu besiegen, der als einer der grössten Gegner in der Finanzwelt gilt. Wir werden versuchen, die Übertagsergebnisse der Währungsvarianten zu prognostizieren. Ich versichere Ihnen: Es ist schwierig, sogar einen Orang-Uan zu schlagen, der zufällig gewettet hat und eine Gewinnrate von 50% hat. Wir verwenden einen vorhandenen Algorithmus, der Vektorklassifikatoren unterstützt. Die SVM-Vektormaschine ist eine unglaublich leistungsfähige Methode zur Lösung von Regressions- und Klassifikationsproblemen.

• SVM unterstützt Vektormaschinen

Die SVM-Vektormaschine basiert auf der Idee, dass wir mit Hilfe einer Überfläche die Eigenschaftsräume von p-Präparaten klassifizieren können. Die SVM-Vektormaschinen-Algorithmen verwenden eine Überfläche und eine Erkennungsmarge, um die Klassifizierungsentscheidungsgrenzen zu erzeugen, wie in der folgenden Abbildung gezeigt.

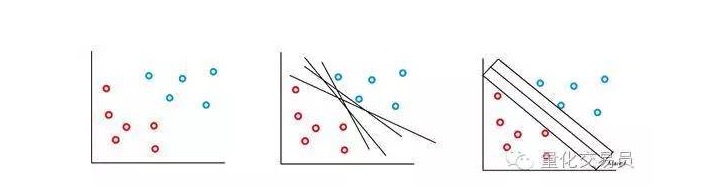
In den einfachsten Fällen ist eine lineare Klassifizierung möglich. Der Algorithmus wählt die Entscheidungsgrenze, die den Abstand zwischen den Klassen maximiert.

In den meisten Finanz-Zeitfolgen, mit denen Sie konfrontiert sind, werden Sie nicht oft einfache, linear trennbare, sondern untrennbare Gruppen finden. Die SVM-Vektormaschine löst dieses Problem durch die Implementierung einer Methode, die als “soft margin method” bezeichnet wird.

In diesem Fall sind einige falsche Klassifizierungen erlaubt, aber sie führen selbst die Funktion aus, um die Faktoren und die Entfernung von den Fehlern zur Grenze zu minimieren, die mit C ((Kosten- oder Budgetfehler sind erlaubt) proportional sind).

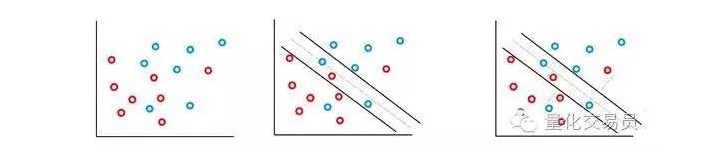
Grundsätzlich maximiert die Maschine den Abstand zwischen den Klassifikationen und reduziert gleichzeitig ihre C-gewichteten Strafen.

Ein tolles Merkmal des SVM-Klassifikators ist, dass die Position und die Größe der Klassifizierungsentscheidungsgrenze nur von Teilen der Daten bestimmt wird, die in der Nähe der Entscheidungsgrenze liegen. Die Eigenschaften dieses Algorithmus ermöglichen ihm, Abweichungen von weit entfernten Abweichungen zu bekämpfen.

Ist das zu kompliziert? Nun, ich denke, der Spaß hat gerade erst begonnen.

Berücksichtigen Sie folgende Situationen (siehe rote Punkte getrennt von Punkten anderer Farben):

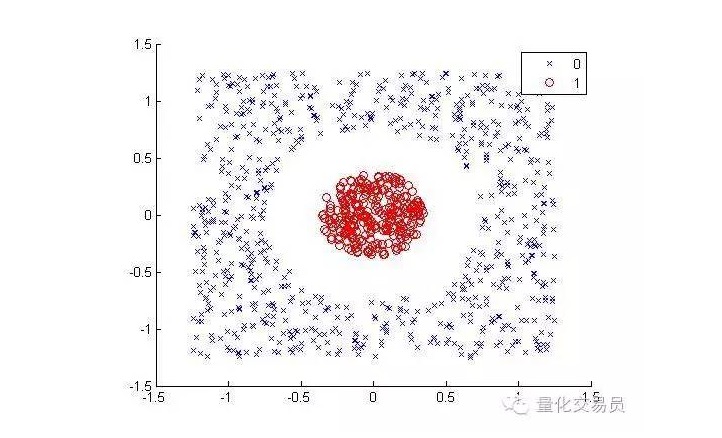
Für den Menschen ist es sehr einfach, es zu klassifizieren. Aber für die Maschine ist es anders. Es ist offensichtlich, dass es nicht zu einer geraden Linie werden kann.

Die Kerntechnik ist eine sehr schlaue mathematische Technik, die es uns ermöglicht, lineare Klassifikationsprobleme in einem hochdimensionalen Raum zu lösen.

Wir werden die zweidimensionale Eigenschaftssphäre in eine dreidimensionale umwandeln, indem wir sie in eine Erhöhungsdimension abbilden, und nach der Klassifizierung in die zweidimensionale zurückkehren.

Die folgenden Grafiken wurden nach der Vergrößerung und nach der Klassifizierung angezeigt:

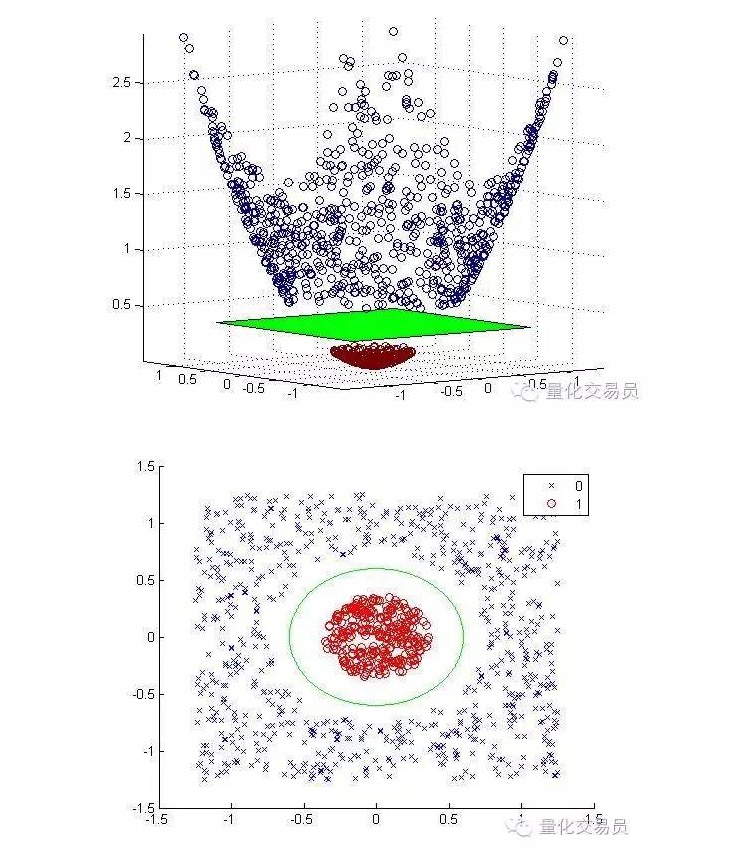
Im Allgemeinen kann man mit einer Karte von einem d-dimensionalen Inputraum in einen p-dimensionalen Feature-Space mit einer D-Inputkarte von einem d-dimensionalen Inputraum in einen p-dimensionalen Feature-Space mit einer D-Inputkarte von einem d-dimensionalen Inputraum mit einer p-dimensionalen Feature-Space abbilden.

Eine wichtige Voraussetzung für diese mathematische Lösung ist, wie man gute Punktesamplesätze im Featurespace erzeugt.

Sie benötigen lediglich diese Punkte-Sample-Sets, um die Grenzoptimierung durchzuführen, die Kartierung muss nicht eindeutig sein, und die Punkte des Eingangsraums in einem hochdimensionalen Featurespace können sicher durch die Kernfunktion ((und ein wenig die Hilfe des Mercer-Theorems)) berechnet werden.

Zum Beispiel, wenn du deine Klassifizierungs-Problematik in einem riesigen Featurespace lösen möchtest, sagen wir 100.000 Dimensionen. Kannst du dir die Rechenleistung vorstellen, die du benötigst? Ich bezweifle sehr, dass du es schaffen wirst.

• Die Herausforderung und der Gorilla

Jetzt sind wir bereit, uns der Herausforderung zu stellen, Jeffs Vorhersagekraft zu besiegen.

Jeff, ein Experte für Geldmärkte, konnte durch Zufallswetten eine Prognose-Genauigkeit von 50% erzielen, die ein Signal für die Vorhersage der Rendite für den nächsten Handelstag ist.

Wir werden verschiedene grundlegende Zeitreihen verwenden, darunter die Zeitreihen für die Preise für die Lieferung, wobei die Zeitreihen jeweils bis zu 10 Lages Gewinne erzielen, insgesamt 55 Features.

Die SVM-Vektormaschine, die wir bauen werden, verwendet einen 3-Deg-Kern. Sie können sich vorstellen, dass die Auswahl eines geeigneten Kerns eine andere sehr schwierige Aufgabe ist. Um die C- und Γ-Parameter zu kalibrieren, wird die 3-fache Kreuzprüfung auf einem Raster möglicher Kombinationen von Parametern ausgeführt, und die beste Gruppe wird ausgewählt.

Die Ergebnisse sind nicht sehr ermutigend:

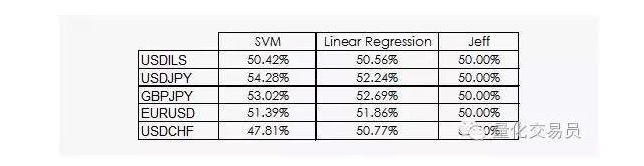
Wir können sehen, dass sowohl die lineare Regression als auch die SVM-Vektormaschine Jeff besiegen können. Obwohl die Ergebnisse nicht optimistisch sind, können wir auch etwas aus den Daten ziehen, was schon gute Nachrichten sind, da in der Datenwissenschaft die finanziellen Zeitreihen nicht die nützlichsten sind

Nach der Cross-Verifizierung werden die Datensätze trainiert und getestet, und wir erfassen die Vorhersagefähigkeit der trainierten SVM. Um eine stabile Leistung zu erzielen, wiederholen wir die 1000-fache zufällige Spaltung jeder Währung.

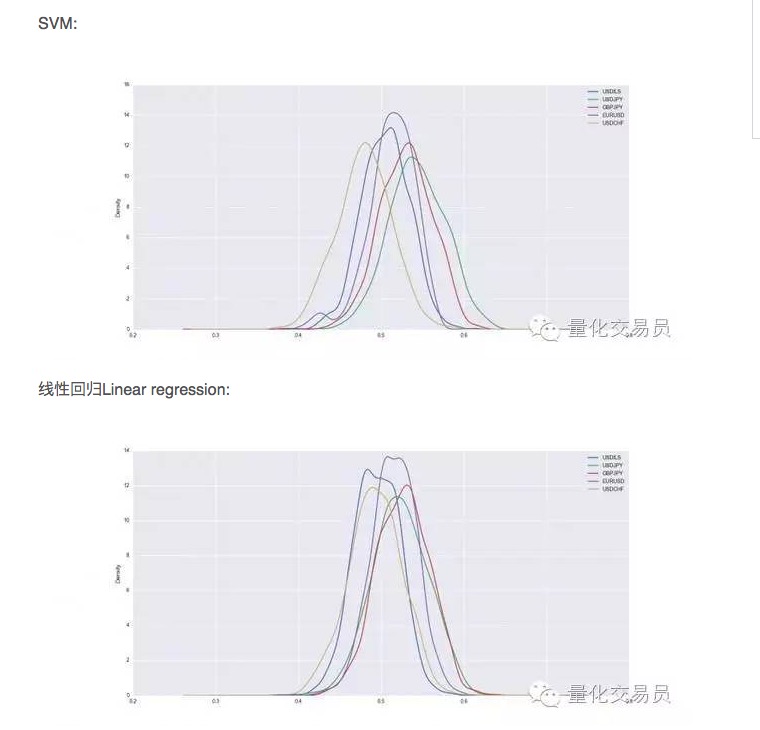
Es scheint, dass die SVM in einigen Fällen besser als einfache lineare Regression ist, aber die Leistungsdifferenz ist auch etwas höher. Bei USD/JPY, zum Beispiel, machen wir durchschnittlich 54% der Gesamtsituationen aus, die wir vorhersagen können. Das ist ein ziemlich gutes Ergebnis, aber lassen Sie es uns genauer betrachten!

Ted ist Jeffs Cousin, der natürlich auch ein Gorilla ist, aber er ist viel intelligenter als Jeff. Ted schaut auf die Trainings-Samplesätze und nicht auf die Zufallswette.

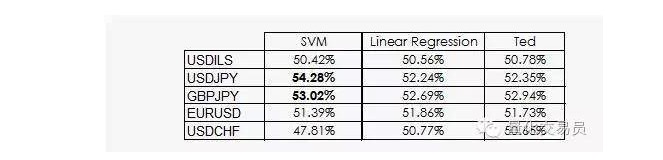
Wie wir gesehen haben, beruht die Leistung der meisten SVMs nur auf der Tatsache, dass die Klassifizierung durch maschinelles Lernen unwahrscheinlich mit der Vorherrschaft gleichzusetzen ist. In der Tat kann die lineare Regression keine Informationen aus dem Merkmalraum erhalten, aber der Intercept ((intercept)) ist in der Regression sinnvoll und die Tatsache, dass der Intercept und die Klassifizierung besser funktionieren, ist relevant.

Ein bisschen gute Nachricht: Die SVM-Vektormaschine ist in der Lage, einige zusätzliche, nicht-lineare Informationen aus den Daten zu gewinnen, die uns eine Prognose-Genauigkeit von 2% geben können.

Unglücklicherweise wissen wir noch nicht, was das für eine Information sein könnte, so wie die SVM-Vektormaschine ihre Hauptnachteile hat, die wir nicht genau erklären können.

Autor: P. López, veröffentlicht in quantdare Übertragung von WeChat Public