Eine Intraday-Strategie, die die Ebenwert-Rückkehr zwischen SPY und IWM verwendet

In diesem Artikel werden wir eine Intraday-Handelsstrategie schreiben. Sie wird die klassische Handlungskonzeption der gleichwertigen Rückkehr von Pfund-Paaren verwenden. In diesem Beispiel werden wir zwei traded-open-end-index-Fonds (ETFs), SPY und IWM, die an der NYSE gehandelt werden, nutzen und versuchen, die US-amerikanischen Aktienindizes zu repräsentieren, die Pfund S&P 500 und Pfund Russell 2000 sind.

Diese Strategie erzeugt eine Gewinndifferenz, indem man mehrere ETFs macht und eine andere ETF leert. Mehrfachverhältnisse können in vielerlei Hinsicht definiert werden, z. B. mit Hilfe einer Methode der statistischen Synchronisierung von Zeitreihen. In diesem Fall berechnen wir durch rollende lineare Regression das Hedge-Ratio zwischen SPY und IWM. Dies wird uns erlauben, eine Gewinndifferenz zwischen SPY und IWM zu erzeugen, die als z-Score standardisiert wird.

Der Grundsatz der Strategie ist, dass SPY und IWM in etwa die gleiche Marktlage repräsentieren, nämlich die Aktienentwicklung einer Gruppe von großen und kleinen US-amerikanischen Unternehmen. Die Voraussetzung ist, dass es immer Rückgänge gibt, wenn man an die regressive Hypothese der Erhöhung der Erhöhung der Preise glaubt, da die Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöhung der Erhöh

Die Strategie

Die Strategie wird in folgenden Schritten umgesetzt:

Daten - von April 2007 bis Februar 2014 erhalten Sie ein 1-minütiges k-String-Diagramm von SPY und IWM.

Verarbeitung - Richtige Ausrichtung der Daten und Löschung von fehlenden k-Strängen.

Differenz - Der Hedging-Verhältnis zwischen den beiden ETFs wird mit einer rollenden linearen Regressionsberechnung berechnet. Es wird definiert als der Regressionskoeffizient β, der mit einem Regressionsfenster verwendet wird, das die K-String 1 nach vorne bewegt und den Regressionskoeffizient neu berechnet. Daher wird der Hedging-Verhältnis βi, der K-String bi-, verwendet, um die K-String zurückzugreifen, indem man den Überschreitungspunkt von bi-1-k bis bi-1 berechnet.

Z-Score - Der Wert der Standarddifferenz wird in der üblichen Weise berechnet. Das bedeutet, dass der Mittelwert der Differenz subtrahiert wird und die Standarddifferenz mit der Differenz subtrahiert wird. Der Grund dafür ist, dass die Schwellenparameter leichter zu verstehen sind, da die Z-Score eine dimensionlose Quantität ist.

Handel - Wenn der negative z-Score unter den vorgeschlagenen (oder nachoptimierten) Threshold fällt, wird ein Mehr- und ein Leersignal erzeugt. Wenn der absolute Wert des z-Scores unter den zusätzlichen Threshold fällt, wird ein Ausgleichssignal erzeugt. Für diese Strategie habe ich (ein bisschen zufällig) die Ausgleichswerte z = 2 als Eröffnungs- und z = 1 als Ausgleichswerte gewählt.

Vielleicht ist es am besten, die Strategie zu verstehen, wenn man sie tatsächlich umsetzt. Im folgenden Abschnitt wird der vollständige Python-Code (ein einzelnes Dokument) für die Implementierung dieser Ebenwert-Rückkehr-Strategie detailliert beschrieben. Ich habe eine detaillierte Code-Anmerkung hinzugefügt, um Ihnen ein besseres Verständnis zu geben.

Implementierung von Python

Wie bei allen Python/pandas-Tutorials muss die Python-Umgebung wie in diesem Tutorial beschrieben eingerichtet werden. Nachdem die Einrichtung abgeschlossen ist, ist die erste Aufgabe, die notwendige Python-Bibliothek zu importieren. Dies ist für die Verwendung von matplotlib und pandas erforderlich.

Die spezifischen Versionen, die ich benutze, sind:

Python - 2.7.3 NumPy - 1.8.0 Pandas - 0.12.0 Matplotlib - 1.1.0

Wir wollen weitermachen und diese Bibliotheken importieren:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Die folgende Funktion create_pairs_dataframe importiert zwei CSV-Dateien mit zwei innerk-Linien, die zwei Symbole enthalten. In unserem Beispiel wird dies SPY und IWM sein. Dann erstellt sie ein separates Data-Pair-Pair, das die Indizes der beiden ursprünglichen Dateien verwendet. Ihre Zeitrahmen können aufgrund von verpassten Transaktionen und Fehlern unterschiedlich sein.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Der nächste Schritt ist eine rollende lineare Regression zwischen SPY und IWM. In diesem Szenario ist IWM der Prognostiker (x) und SPY die Antwort (y). Ich habe ein Default-Regressionsfenster mit 100 k-Zügen eingerichtet. Wie oben erwähnt, ist dies ein Parameter der Strategie. Damit die Strategie als stabil angesehen wird, möchten wir idealerweise sehen, dass ein zurückgegebener Bericht in der Regressionsphase die Kondensfunktion (x) oder andere Leistungsmetriken darstellt.

Nach der Berechnung der Roll-β-Koeffizienten im linearen Regressionsmodell von SPY-IWM wird das zu den DataFrame-Paaren hinzugefügt und die Leerzeilen entfernt. Das bildet die erste Gruppe von K-Linien, die einem Schnittmaß für die Rücklauflänge entspricht. Dann erstellen wir zwei ETF-Gewinndifferenzen in Einheiten von SPY und Einheiten von -βi von IWM. Offensichtlich ist dies nicht realistisch, da wir eine geringe Anzahl von IWM verwenden, was in einer realen Implementierung nicht möglich ist.

Zu guter Letzt erstellen wir den Z-Score der Zinsspanne, der durch Subtrahieren der Mittelwerte der Zinsspanne und Berechnung der Standardsspanne der Standardsspanne berechnet wird. Es ist zu beachten, dass hier eine ziemlich subtile Vorwegnahme-Zinsspanne vorhanden ist. Ich habe sie absichtlich im Code gelassen, weil ich betonen wollte, wie leicht es ist, solche Fehler in der Forschung zu machen.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

In create_long_short_market_signals werden Handelssignale erstellt. Diese werden berechnet, indem der Wert der z-Score die Schwelle übersteigt. Ein Ausgleichssignal wird gegeben, wenn der absolute Wert der z-Score kleiner als oder gleich einer anderen (kleinen) Schwelle ist.

Um dies zu erreichen, ist es notwendig, für jede k-String eine Handelsstrategie festzulegen, ob es sich um einen offenen oder einen flachen Lagerstück handelt. Long_market und short_market sind die beiden definierten Variablen, die für die Verfolgung von Multi- und Leerstandpositionen verwendet werden. Leider ist die Programmierung in iterativer Weise einfacher und daher langsamer als bei der Quantifizierungsmethode. Obwohl ein 1-minütiger k-String-Diagramm etwa 700.000 Datenpunkte pro CSV-Datei benötigt, wird er auf meinem alten Desktop immer noch relativ schnell berechnet!

Um einen pandas DataFrame zu iterieren (was sicherlich eine ungewöhnliche Operation ist), ist es notwendig, die iterrows-Methode zu verwenden, die einen iterativen Generator bietet:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

In dieser Phase haben wir die Paare aktualisiert, um tatsächliche Mehr, leere Signale zu enthalten, die uns in die Lage versetzen, festzustellen, ob wir eine Position einnehmen müssen. Jetzt müssen wir ein Portfolio erstellen, um den Marktwert der Position zu verfolgen. Die erste Aufgabe besteht darin, eine Position zu erstellen, die mehrere Signale und leere Signale kombiniert.

Sobald der Marktwert des ETFs erstellt wurde, haben wir sie zusammengefasst, um den Gesamtmarktwert am Ende jeder k-Zeile zu ergeben. Dann wurde dieser durch die pct_change-Methode des Objekts in einen Rückwert umgewandelt. Die folgenden Codezeilen haben die falschen Elemente (NaN und inf-Elemente) beseitigt und schließlich die vollständige Anspruchskurve berechnet.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Die Hauptfunktion verbindet sie miteinander. Die CSV-Dateien innerhalb des Tages befinden sich im Datadir-Pfad. Bitte ändern Sie den folgenden Code, um auf Ihren spezifischen Verzeichnis zu verweisen.

Um zu bestimmen, wie empfindlich die Strategie für die Lookback-Zyklen ist, ist es notwendig, eine Reihe von Lookback-Leistungsindikatoren zu berechnen. Ich habe die endgültige Gesamtrendite des Portfolios als Performance-Anzeige und den Lookback-Bereich[50,200] gewählt, der mit einer Inkrementalzahl von 10 ist.

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

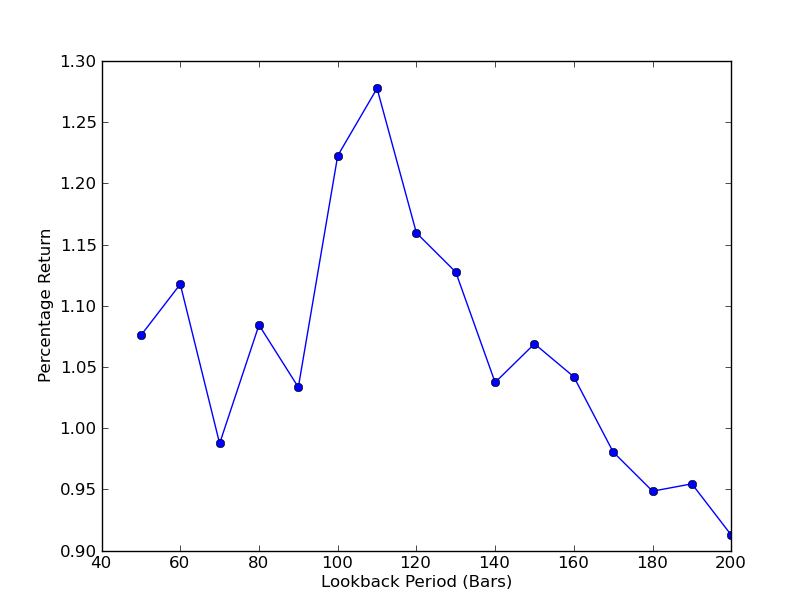
Sie können nun ein Diagramm von Lookbacks und Returns sehen. Bitte beachten Sie, dass Lookbacks eine maximale Panoramaschwelle haben, die 110 k-Zeichen entspricht.

SPY-IWM-Lineare Regressions-Hedging gegenüber Lookback-Perioden-Sensitivitätsanalyse

Ohne eine nach oben gerichtete Gewinnkurve ist jeder Rückblick Artikel unvollständig! Wenn Sie also eine Kurve der kumulierten Gewinnrendite und der Zeit ziehen möchten, können Sie den folgenden Code verwenden. Es wird das endgültige Portfolio, das aus der Untersuchung der Lookback-Parameter erzeugt wurde, darstellen. Daher ist es notwendig, einen Lookback auszuwählen, je nachdem, wie Sie es visualisieren möchten.

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

Die Lookback-Periode für die folgenden Vermögens- und Nutzenkurven ist 100 Tage:

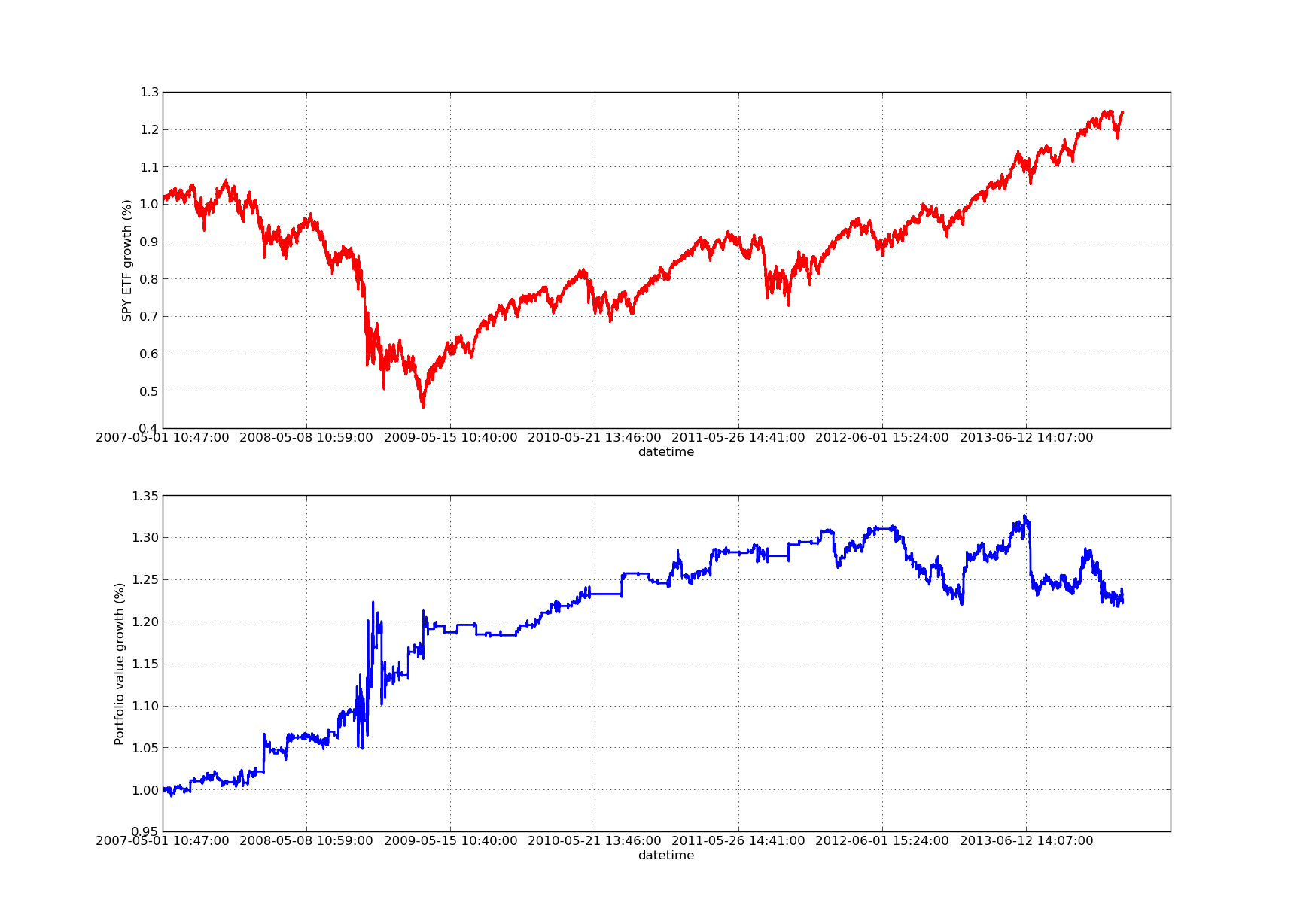
SPY-IWM-Lineare Regressions-Hedging gegenüber Lookback-Perioden-Sensitivitätsanalyse

Bitte beachten Sie, dass die SPY 2009 während der Finanzkrise stark zurückgegangen ist. Die Strategie befindet sich auch in dieser Phase in einer unruhigen Phase. Bitte beachten Sie auch, dass sich die Ergebnisse im vergangenen Jahr verschlechtert haben, da die SPY in dieser Zeit eine stark trendorientierte Natur hatte, die den S&P 500 widerspiegelte.

Bitte beachten Sie, dass wir bei der Berechnung der Z-Score-Gewinnspanne immer noch die Prognose-Abweichung berücksichtigen müssen. Außerdem wurden alle diese Berechnungen ohne Transaktionskosten durchgeführt. Diese Strategie wird sicherlich schlecht abschneiden, wenn man diese Faktoren berücksichtigt.

In einem späteren Artikel werden wir einen komplexeren, ereignisgetriebenen Backtester erstellen, der diese Faktoren berücksichtigt, um uns mehr Vertrauen in die Kapitalkurve und die Performance-Indikatoren zu geben.