Can you run over a gorilla with an SVM vector machine?

Can you run over a gorilla with an SVM vector machine?

Ladies and gentlemen, place your bets. Today, we will do our best to defeat an orange, which is considered one of the most fearsome opponents in the financial world. We're going to try to predict the next day's returns of the currency trading varieties. I assure you: even trying to beat a random bet and get a 50% chance of winning is a difficult task. We will use a ready-made machine learning algorithm that supports vector classifiers. SVM vector machines are an incredibly powerful method for solving regression and classification tasks.

• SVM support for vector machines

The SVM vector machine is based on the idea that we can classify the characteristic space in p-dimensional versus hyperplanes. The SVM vector machine algorithm uses a hyperplane and a resolution margin to create a classification decision boundary, as shown below.

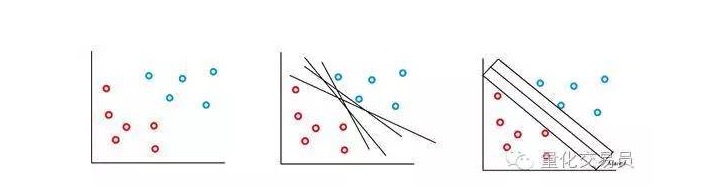
In the simplest case, linear classification is possible. The algorithm selects the decision boundary, which maximizes the distance between classes.

In most financial time series you will not encounter simple, linear separable sets, and inseparable ones will often occur. The SVM vector solves this problem by implementing a method known as the soft margin method.

In this case, some error classification situations are allowed, but they themselves perform functions to minimize the distance between the factors and errors to the boundary of the ratio with C (an error in the cost or budget can be allowed).

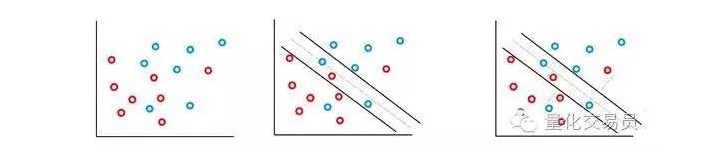
Basically, the machine will try to maximize the interval between classifications while minimizing its C-weighted penalty items.

An excellent feature of the SVM classifier is that the location and size of the decision boundary is determined only by a fraction of the data, i.e. the part of the data that is closest to the decision boundary. The characteristics of this algorithm allow it to withstand interference from abnormal values at distant intervals.

Is it too complicated? Well, I think the fun is just beginning.

Consider the following situation (separate red dots from other colored dots):

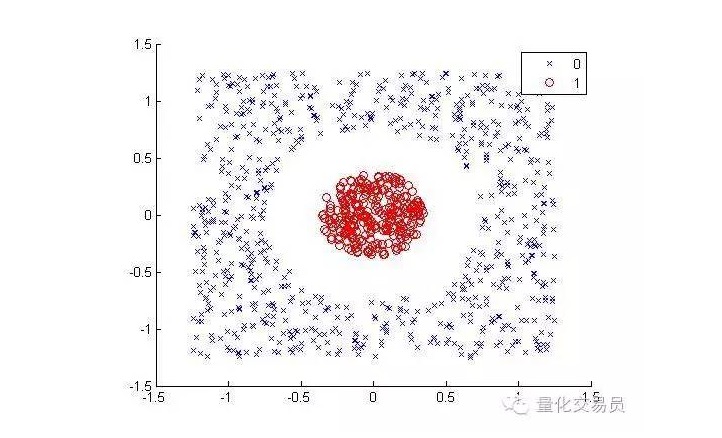
From a human point of view, it is very simple to classify (even an elliptical line); but it is not the same for a machine. Obviously, it cannot be made into a straight line (a straight line cannot separate the red dots). Here we can try the kernel trick.

The kernel technique is a very clever mathematical technique that allows us to solve linear classification problems in high-dimensional space. Now let's see how it's done.

We will convert the two-dimensional feature space into three dimensions by elevation mapping, and return to two dimensions after the classification is complete.

Below is a graph of the elevated-dimensional mapping and after-classification:

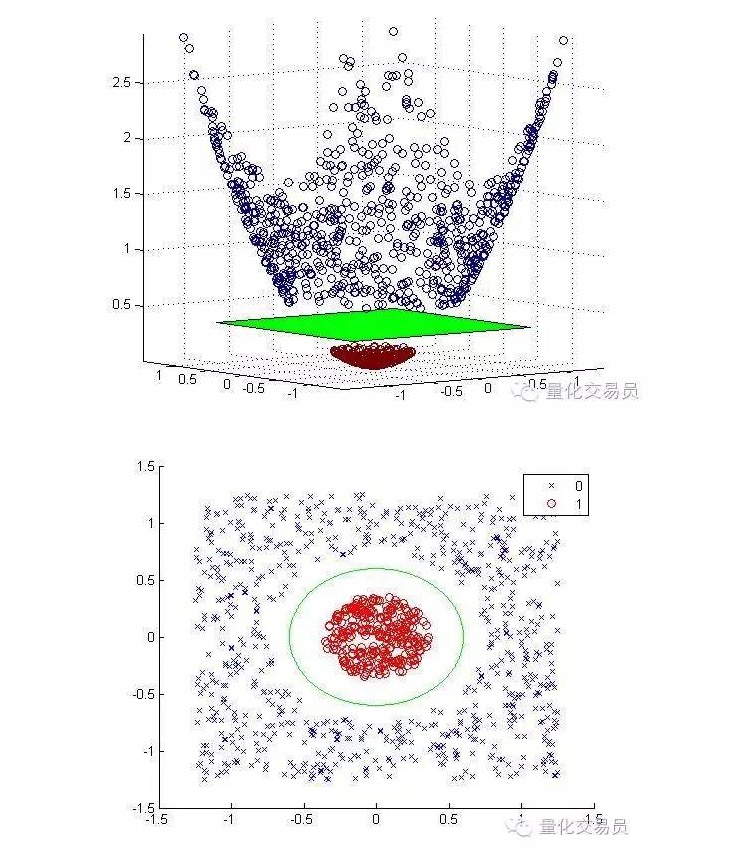
In general, if there is d input, you can use a mapping from the d-dimensional input space to the p-dimensional feature space. Run the solution that the above minimization algorithm will generate, and then map back to your original p-dimensional superplane of the input space.

An important premise of the above mathematical solution is that it depends on how to generate a good set of point samples in the feature space.

You only need these point sample sets to perform boundary optimization, the mapping does not need to be explicit, and the points of the input space in the high-dimensional feature space can be safely calculated with the help of the kernel function ((and a bit of Mercer's theorem)).

For example, you want to solve your classification problem in a super-large feature space, say 100,000 dimensions. Can you imagine the computational power you need? I'm very skeptical that you can do it. Well, the kernel now lets you compute these point samples, so this edge is from your comfortable low-density input space.

• Challenges and gorillas

Now we are ready to face the challenge of defeating Jeff's predictive abilities.

Jeff is an expert in the money market, and he is able to get a 50% prediction accuracy by betting randomly, which is a signal to predict the next trading day's yield.

We will use different basic time sequences, including the spot price time sequence, with up to 10 lags of gain for each time sequence, for a total of 55 features.

The SVM vector machine we are about to build uses a 3-degree kernel. You can imagine that selecting a suitable kernel is another very difficult task, in order to calibrate the C and Γ parameters, 3-fold cross-validation runs on a grid of possible parameter combinations, and the best set will be selected.

The results are not very encouraging:

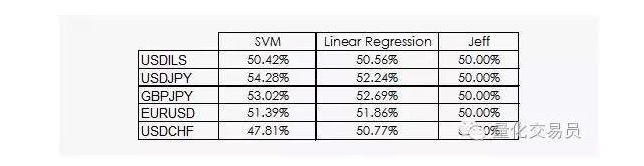
We can see that both linear regression and SVM vector machines can beat Jeff. Although the results are not optimistic, we can also extract some information from the data, which is already good news, because in the data science, the daily gains of financial time series are not the most useful.

After cross-validation, the dataset will be trained and tested, and we record the predictive power of the trained SVM, repeating the random split of each currency 1000 times in order to have a stable performance.

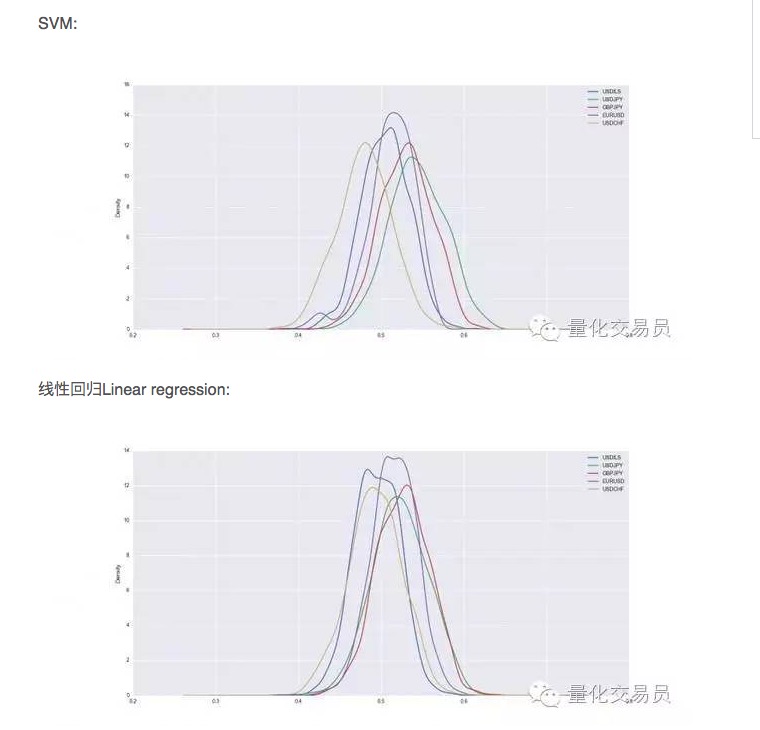
So it looks like SVM is better than simple linear regression in some cases, but the performance difference is also slightly higher. In USD/JPY, for example, we can predict an average of 54% of the total number of signals.

Ted is Jeff's cousin, which is of course also a gorilla, but it's smarter than Jeff.

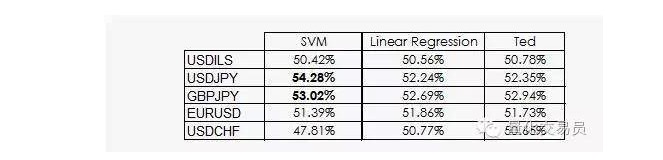
As we have seen, the performance of most SVMs comes from the simple fact that machine learning to classification is unlikely to be equal to precedent. In fact, linear regression cannot get any information from the feature space, but intercepts are meaningful in regression, and intercepts are related to the fact that one classification performs better than another.

The slightly better news is that the SVM vector is able to extract some extra non-linear information from the data, which allows us to suggest a prediction accuracy of 2%.

Unfortunately, we don't yet know what kind of information this might be, as the SVM vector machine has its own major disadvantages that we can't explain clearly.

Author: P. López, published in Quantdare Translated from WeChat