Math and gambling (1)

Math and gambling

• We know that gambling is a game of probability, and it is some strange gambling results that attracted the interest of the mathematician Pascal and the great mathematician Fermat, who, through correspondence, proposed some principles of probability theory, thus creating the theory of probability.

• The perfect gambler.

The NBA team Lakers and Cowboys have a game, and both teams have loyal fans, so call them Monkey Monkeys and Monkey Monkeys. The fans of course feel that the team they support is more likely to win, so they are willing to bet with you. Suppose that Monkey Monkeys think that the probability of the Lakers winning is p, and Monkey Monkeys think that the probability of the Cowboys winning is q, p and q should be greater than 50%.

The method is as follows: we bet the same pot with the monkey monkey and the monkey monkey, respectively, and if we win we get y, if we lose we lose x, as long as y > x we win. And x and y only need to satisfy the following two simple inequalities, and the expected return of the monkey monkey and the monkey monkey will be positive:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

Adding the constraint of y>x, the drawn image is the area surrounded by three straight lines, and the coordinate value ((x,y) for any point in it is a win-win solution. If p>q, the solution is the blue part of the diagram below:

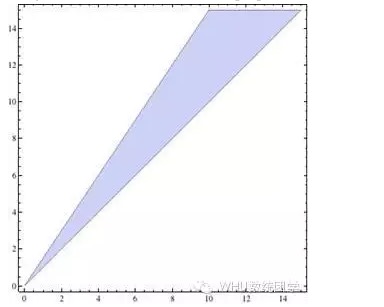
The problem seems to be solved perfectly, but there is a doubt, which I believe the reader will soon discover to be absurd: whether it's the ape or the ape, their expectations of returns are positive, that is, in the long run they will make money, and we are stable, where does the money come from, how can everyone make money?

• Two or three card scams

  

This is another clever conundrum, where we have three cards, one of which is black on the face, two of which are red on the face, and three of which are black on one side and red on the other. Then we put the cards in a box, shake them, and have the opponent draw a square on the table. Then he and his opponent draw the same color as the face. This conundrum seems fair, for example, if one surface is black, then the card is not 1 or 3, and the opposite color is not black or red, with an intuitive probability of 1/2.

In fact, the odds of us winning are not 1/2, but 2/3, and the most confusing part of this stalemate is the two-sided deck of cards. The player draws not three cards, but six faces: three black faces, three red faces.

When the player draws the black side, the three possible situations are A, C, D, and so on, and their backs are D, F, and A respectively, with black accounting for 2/3 of the situation.

The problem was first posed in 1889 by French mathematician Joseph Louis François Bertrand, and is also known as Bertrand's box paradox because of its surprising results. In 1950, American mathematician Warren Weaver introduced the above card game, which Martin Gardner called the three-card swindle.

• Three, such an unusual black peach A.

  

  Sometimes we start the game with a little water, and then we let someone else make a little money, and then we stretch the line, and then we get a net. This is a great example. Four people are playing bridge, and I say, "Hey, let's play a net, I have an A now, guess I have more A's?"

  Many people will probably think that the two eggs are no different, and that adding a black peach doesn't matter. But the difference between them is unbelievable. Let's start with the probability of the first egg:

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：
  
  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%
  

  At this time I was going to bet on myself and A, which is easier to lose. But after the first bet, everyone's willingness to bet was mobilized, at first glance the second bet was not changed clothes, they increased the bet, then I did not have more A, right in the middle of us. Below we will find that the probability of the second bet is very different:

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：
  
  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。
  

Translated from WHU Arithmetic