How the Bitcoin protocol works

How the Bitcoin protocol works

I wrote five thoughts about Bitcoin last year, which seems to be the first article on Bitcoin here, and today I'm going to talk about the Bitcoin protocol here.

This article is a translation of Michael Nielsen's article on the Bitcoin protocol, which the translator feels is the clearest article about Bitcoin ever written. Michael Nielsen is a pioneering scientist, writer and programmer in the field of quantum computing. The details of this article are to be found in his own introduction. This article is translated because the translator believes that there are many, many supportive objections to the article and discussion about Bitcoin. But most of them stay on the concept, price and subjective thinking.

It would help to condense the article and make it less promotional sounding as soon as possible. Just letting people know what it is, where it fits into the electronic money space, not trying to convince them that it's good.

• Here is the full text:

  Thousands of articles have attempted to explain Bitcoin, an online, peer-to-peer currency. Most of the articles are full of details about the underlying protocol, omitting many details. Even the in-depth articles are stuck in key places. The purpose of this article is to explain the basics behind the Bitcoin protocol in the clearest, most understandable way possible.

  Deep understanding of the protocol is difficult because it's easy to take Bitcoin for granted and think about how to use it to speculate on how to make money, think about whether it's a bubble, think about whether Bitcoin means the end of taxation, etc. These are interesting to think about, but these ideas seriously limit your understanding. Understanding the protocol itself will open up other avenues that are not accessible. For example, the protocol is the basis of the scripting language built into Bitcoin, which allows you to create new financial instruments with Bitcoin, such as smart contracts.

  I'll explain Bitcoin scripts and smart contracts in a later article. This article will focus on the specifics of the Bitcoin protocol. To understand this article, you'll probably need to be familiar with public key passwords and their associated digital signatures. You'll also need to be familiar with hash functions (converting input of arbitrary length into output of fixed length).

  Bitcoin is based on cryptography, which may surprise you, but is it not a currency? Is it a way of sending secret messages? In fact, the problem that Bitcoin wants to solve is mostly about protecting transactions by ensuring that people cannot steal things from others or impersonate others, etc. In the physical world of atoms, we ensure security through locks, signatures, bank insurance boxes, etc. In the information world, we ensure security through cryptography. That's why Bitcoin is the core cryptographic protocol.

  The strategy of this article is to build Bitcoin layer by layer. We'll start with a very simple digital currency, which we'll temporarily call the Infocoin chip, to distinguish it from Bitcoin. Of course, our first version of Infocoin will have many drawbacks, so we'll go through several iterations, each introducing one or two new concepts. After several iterations, we'll have a complete bitcoin protocol.

  This approach is a bit slower than explaining Bitcoin directly from the beginning. But even if you can understand the principle of Bitcoin, it is difficult to understand why Bitcoin is designed this way. The advantage of a slow step-by-step iterative explanation is that it allows you to have a clearer understanding of every element of Bitcoin.

  Finally, I should say that I am a relative newcomer to the Bitcoin world. I had a rough focus in 2011, but I really looked into the details in early 2013.

• Step 1: Sign the letter of intent

  • How do you design a currency?

    On the surface, a digital currency sounds impossible. Suppose a person we call Alice has some digital currency that she wants to spend. If Alice can use a string of characters as money, how can we stop her from using the same string repeatedly?

    These are just two of the many problems to be solved with information as currency. In the first version of Infocoin, we tried to get Alice to provide a string as money, and to think of a way to protect it from being counterfeited. Suppose Alice was going to give an infocoin to another person, Bob.

    This method is not very popular, but it still has some advantages. Anyone in the world can use Alice's public key to verify that Alice is indeed the person who signed it. No one else can produce the result of that signature. (This signature can only be generated from the private key that Alice has, see the digital signature mentioned above), so Alice can't go back and say no. I didn't give Bob the infocoin.

    I haven't told you what the money in the protocol is. What is clear is that the money is the message itself. That is to say, the number of signatures represents the number of characters that Alice is going to give Bob. The future protocol will be similar in that all digital currencies are just increasingly detailed message characters.

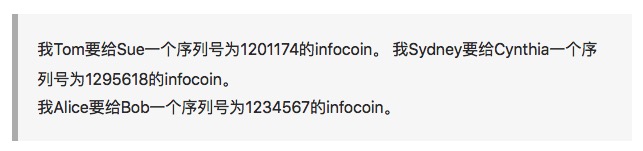
• A serial number is used to uniquely identify the currency.

  The problem with our first version of Infocoin was that Alice could repeatedly send the same signed message to Bob. Suppose Bob received 10 such messages: "Give me, Alice, one infocoin". Is it that Alice gave Bob 10 different infocoins? Or did Alice give Bob one infocoin and just repeat the message carelessly?

  We want the infocoin to have a unique identifier. It needs a tag or a serial number. Alice can sign the infocoin tag with the serial number 8740348 in the message box. Then, if Alice signs the infocoin tag with the serial number 8770431 in another message, Alice can sign the infocoin tag with the serial number 8770431 in the message box, so that Bob and everyone else will know that there are two different infocoins.

  For this scheme to work, we need a credible source of serial numbers. One way to generate a serial number is to set up an institution like a bank. This bank will generate a serial number for the infocoin, record who owns which infocoin, and verify the authenticity of the transaction.

  In more detail, let's say Alice goes to a bank and says, "Hey, I'm going to take an infocoin out of my account". The bank subtracts an infocoin from her account, and then gives her a new, never-used serial number, let's say 1234567. Then, when Alice wants to send an infocoin to Bob, she signs this new message to me, "Hey, Alice is going to give Bob an infocoin with the serial number 1234567.

• Let everyone be a bank

  The above solution seems to have a lot of potential. However, we can do something more ambitious. We can remove banks from the agreement. This drastically changes the properties of the currency itself. This means that there will be no separate organization in charge of the currency.

  The method is to have everyone cooperate to become a bank. In particular, we assume that every person who uses an infocoin keeps a complete record, including which infocoin belongs to which person. You can think of it as a shared public ledger, which records the transaction records of all the infocoins.

  Now let's say that Alice is going to give Bob an infocoin. She's going to send me a message saying that Alice is going to give Bob a signed infocoin string with the serial number 1234567. And she's going to send the signed message out to Bob, and Bob can check it with his own blockchain. OK, that's the infocoin that Alice gave me.

  We still have the issue of where the infocoin sequence number came from, but this is actually easy to solve, so I'll explain later. The more difficult problem is that this protocol allows Alice to repeatedly spend her infocoin. She can publish a signed message saying that Alice is going to give Bob an infocoin sequence number 1234567. She can also publish a signed message saying that Alice is going to give Charlie an infocoin sequence number 1234567. Bob and Charlie both use their own blockchain to check that the infocoin is indeed from Alice.

  We call this problem the double spending dilemma, and at first glance, it seems difficult to succeed. After all, if Alice sends the message to Bob first, and then Bob sends the message to everyone else, including Charlie, the others update their blockchain. At this point, Charlie is not fooled by Alice. So it seems that double spending is only possible in a short period of time. However, even if this time is short, this problem is also undesirable.

  The easiest way to solve this problem is that when Alice sends infocoin to Bob, Bob should not check the transaction alone. Instead, he should publish the pending transaction to the entire infocoin network, and let others help judge whether the transaction is legitimate. If they jointly decide that the transaction is legitimate, then Bob can accept the infocoin, and then everyone updates their blockchain.

  More specifically, let's say Alice wants to give Bob an infocoin. As before, she signs a message, and then Alice will give Bob an infocoin token with the serial number 1234567, and sign the message to Bob. Also, as before, Bob uses his own blockchain to make a check, and the coin does indeed belong to Alice. But the protocol is different, Bob does not accept this directly, but publishes Alice's message to the entire network.

  There are still many uncertainties about the protocol; for example, what does it mean when enough people publish the message, how many people are enough? It can't be the entire infocoin network because we don't know who is on the infocoin network in advance. Also, it can't be a fixed part of the user base.

• Proof of work

  Suppose Alice wants to double-click on the above protocol, he needs to take control of the entire infocoin network. Suppose she uses an automated system to create many accounts with different identities on the infocoin network, let's say a billion. As before, she tries to double-click, giving the same infocoin to Bob and Charlie, but when Bob and Charlie ask the infocoin network to verify the transaction, Alice's donkeys flood the entire network, telling Bob and Charlie they can go through the transaction, and may deceive either one of them or both of them to accept the transaction.

  There's a clever way to do this, using a method called Proof-of-work checking. The method is not intuitive and requires a combination of two concepts: 1) making the process of checking a transaction cost a lot of computational overhead; 2) rewarding them for helping to verify the transaction.

  That's the point of the job description. But to really understand the job description, we need to go into more detail.

  Let's say that Alice is going to give Bob an infocoin with the serial number 1234567. When everyone else on the network hears this message, everyone adds it to a list of pending transactions, none of which have yet been approved by the entire network.

  

  David checks his own blockchain and sees that the above transactions are legitimate. He wants to help spread this verification message throughout the network. However, before that, the verification transaction protocol requires David to solve a computational conundrum called a proof of work. If he does not get the solution to the conundrum, the other members of the network will not accept his verification.

  To explain this, we include it in the protocol itself with a fixed hash function known to everyone on the network, the hash function string. Bitcoin uses a well-known SHA-256 hash function, but any cryptographic hash function can be used here. We give this group of pending transactions a tag, a L tag, for later reference. This group of pending transactions is also equivalent to a block in the blockchain.

  

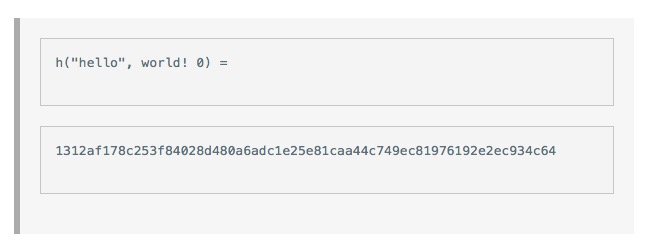
  The problem that David will solve is to find a random number x, and when we add this x to the L and hash this combination, the result starts with a few 0s. The difficulty of this problem can be adjusted by adjusting the number of zeroes that start. A simple hash function needs only 3 or 4 zero-started hashes, while a difficult hash function may require more zero-started hashes, say 15 consecutive zeros.

  And you can see that this doesn't work when x equals 1.

  

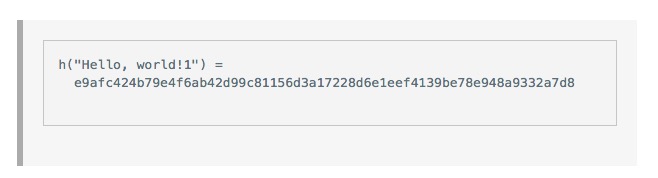
  And then we try x is equal to 2, and then x is equal to 3, 4, 5, and finally, when we find x is equal to 4350, we get

  

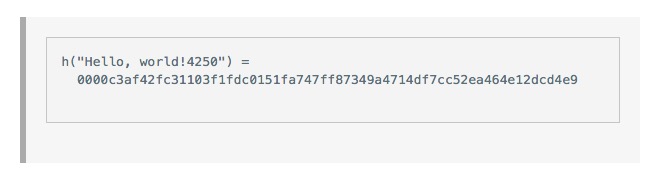
  This random number x gives us a result of four zero-beginning hashes. This is enough to solve a simple hash function to prove hash.

  What makes this problem difficult to solve is that the result of the hash function is always random, and any slight change to the input value will completely change the output of the entire hash function, so it is difficult to predict. So if we need to output a result that has to start with 10 zeros, then David would need on average 1610 ≈ 1012 different x's to find the right value. This is a very challenging task that requires a lot of computational power.

  Obviously, we can control the difficulty of the proof-of-work problem by specifying how many zeros are needed. In fact, the Bitcoin protocol has a better control over the difficulty of the problem by slightly modifying the above proof-of-work. It is no longer a requirement to specify how many starting zeros are needed, but rather to specify that the hash output of the block is less than or equal to a target value, which is automatically adjusted to ensure that each block of Bitcoin takes an average of 10 minutes to solve.

  Well, let's assume David is lucky enough to find a suitable x (nonce), congratulate him! (he will be rewarded for finding this answer). He will publish that he has proven the transactions in this block to be valid, and at the same time publish the value of the x that she has found, so that other participants in the infocoin can prove that the proof of work of x is valid.

  In order for this scheme to work, network participants should need an incentive mechanism to help verify the transaction. Without an incentive mechanism, no one would be willing to spend their computer computing power to help verify the transaction. If network participants are unwilling to spend computing power, the whole system will not work. Therefore, we can reward anyone who successfully verifies the transaction by giving them some infocoin.

  In Bitcoin's protocol, this verification process is known as a "mining" process. The successful verifier of each transaction block receives a Bitcoin as a reward. Initially, it is a reward of 50 Bitcoins per 210,000 verified blocks (that is, approximately every 4 years), but the reward is halved. So far, this has only happened once, i.e. now the verification of a block receives a reward of 25 Bitcoins. The halving process will continue until about 2140 when the mining reward will be reduced to 10-8 Bitcoins.

  You can think of proof-of-work as a process of competitive verification of a transaction. Each participant spends a fraction of the computing power. A miner's chance of winning is roughly equal to the ratio of the computing power they control to the computing power of the entire network. For example, if a miner controls one percent of the computing power of the entire network, then his probability of winning is roughly one percent.

  Of course, even if dishonest miners have a small chance of breaking the entire blockchain, we are not confident enough to use it as currency.

  I'm going to analyze the problem of double flowering right away, but before that, I want to add an important detail to the concept of Infocoin. Ideally, we want the Infocoin network to be able to unify the order in which transactions occur. If we don't have a unified order, it's not clear who has which infocoin at any given time. To help solve this, we require that the new block must contain a pointer to the top of a block, which is actually the hash result of a block.

  

  In a random event, a blockchain will branch out. This is because sometimes two miners verify a transaction in a block almost simultaneously. They publish it to the network at the same time. Some people update their blockchain in one way, others update their blockchain in another.

  

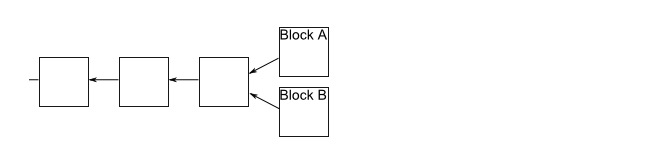
  This creates a situation that we want to avoid, where the order of transactions is not clear, and who has which infocoin is not clear. Fortunately, there is a simple way to move branches. The rule is this: if a branch situation occurs, then people on the network continue to keep two branches, and in any case, miners only work on the longest blockchain.

  Let's say we have a branch and some miners get to block A first, and other miners get to block B first. Those miners who get to block A will continue to mine along their branch, and others will mine along the branch of block B. Let's say that the miners on branch B successfully mine the next block first:

  

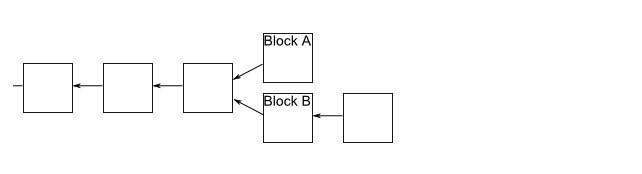
  When they receive this message, the people in Branch A will notice that Branch B is the longest now, so they will switch to Branch B. Work on Branch A will stop quickly, so everyone will be working on the same sequence of blockchains. Then block A will be ignored. Of course, all pending transactions in block A will remain pending, and then will be placed in a new block on Branch B, so that all transactions will eventually be verified.

  Similarly, if the miner on Branch A digs the next block first, then the person working on Branch B stops and moves to Branch A.

  Regardless of the outcome, this process ensures that the blockchain has a unified order. In Bitcoin, a transaction does not count as confirmed until 1) it exists in the block in the longest branch, and 2) at least 5 verified blocks are verified behind it. In this case, we say that the transaction has 6 confirmed blocks.

  Now that we understand the time sequence, let's go back to thinking about what would happen if a dishonest person wanted to double-spend. Suppose Alice was to give Bob and Charlie the same transaction at the same time. One possibility is to have her verify a block with two transactions at the same time. Suppose she had one percent of the computational ability, then she might have been more fortunate to verify this one block. Unfortunately, this double-spending would be immediately discovered and rejected by others, although she solved the difficult problem in the proof of work. So we don't have to worry about that possibility.

  But another possibility is that she is trying to publish two transactions separately. She may publish one transaction to one miner and another to another miner, and she wants both transactions to be verified. Fortunately, in this case, as we just said, the network will end up confirming only one of the transactions. So, this is not a problem either.

  Another possibility is that Alice = Bob, which means that Alice tries to give a coin to Charlie, and she also tries to give that coin to herself, since she can have multiple accounts herself. In this case, Alice's strategy is to wait until Charlie accepts the Infocoin, which is probably after the transaction has been confirmed six times on the longest blockchain.

  

  Unfortunately, by this time, Alice is already six steps behind the longest blockchain. She has a hard time keeping up with the longest branch. The other miners won't help her because they all need to work on the longest branch to be rewarded. Unless Alice is able to combine faster than others on the network when it comes to solving proof-of-work problems (i.e. she probably has more than 50% of the computational power of the entire network).

  Of course, this is not very strictly to say that Alice can't be double-crossed. This is just a reasonable inference. The original Bitcoin white paper did not conduct a rigorous security analysis, but only an informal inference similar to mine.

  This is the first half, and the second half, where author Michael leaves the concept of Infocoin aside to explain the Bitcoin protocol in more detail through the eyes of Bitcoin traders.

  Also, if you find it helpful, I suggest you tip the author of this article, Michael Nielsen, at 17ukkKt1bNLAqdJ1QQv8v9Askr6vy3MzTZ, or follow him on Twitter.

This article is adapted from the booklet Young People Ask.