The rules of trading are detailed in the scientific principles of stable profitability
Author: iyth888, Created: 2021-07-16 19:36:02, Updated: 2021-07-17 10:25:36PS: This article is quite long, it is not a big deal, I recommend you to read it patiently, it will be helpful for you.
Net trading is essentially a method of trading that involves the mechanical manipulation of price fluctuations by means of repetitive low buy high sell. When prices fall, segmented buying is done, and when prices rise, segmented selling is done. Net trading is not dependent on artificial thinking, it is a purely procedural behavior, like a fishing net, using the market's fluctuations to buy low and sell high within the grid area, and to make a profit by repeatedly cycling price differences.
The network trading method can be programmatically operated, without spending time on long-term speculation, and is safe and secure. The network trading method is therefore the most suitable way to participate in stable profits for ordinary people, because this method requires low skills and experience, is very versatile, and is especially suitable for friends who cannot make money in the stock market.
The rules of the grid trading law are detailed
A simple analogy is to divide your money into two equal parts: one part immediately bought into your preferred stock or fund, and the other part put in your pocket as a reserve. If the stock or fund you buy keeps going down, you take the money out of your pocket and put it into the stock market; on the contrary, if the stock or fund you buy runs out, you sell a part of it and put the money in your pocket. Many trading software are built-in with specific rules, and users can automate the operation with a simple setup. The articles in the Grid Trading Law Universe column series have setup tutorials, and interested friends can search for the content of the column and directly learn the software setup tutorial.
There are many variations of the network trading method, but here is one of the most famous, the scientific principles of how to make money on a stable basis and explain why you will have more and more money in your account.
Every idiot has had this experience, a stock is not easy to go up, then fall back to its original price, a hard time, secretly regret, sell early. In fact, without regrets, one of the world's greatest scientists information about the inventor Shannon helped us figure out the solution.
In his later years, Shannon focused on investing research and gave a series of lectures on how to make money. One year, Shannon gave a talk in the largest auditorium at MIT on how to make money in these circumstances.
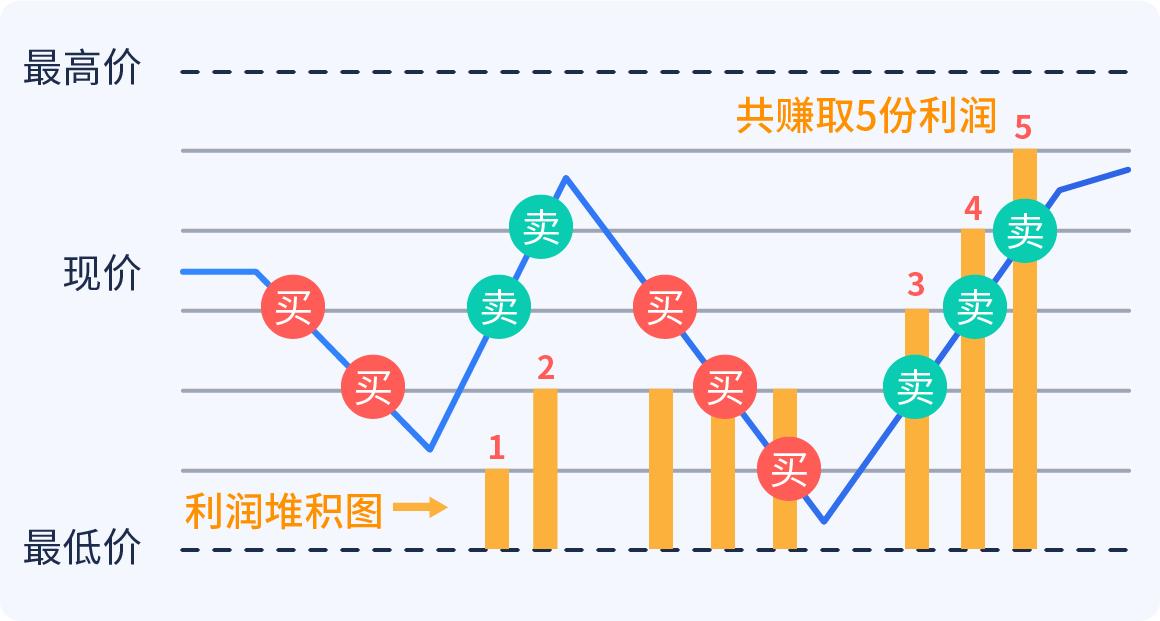
The people behind this recipe call it Shannon's Devil, which is a commonly used form of grid trading.
Shannon's secret is as follows:
What if a stock went up from one to two and then down from two to one?
If you're willing to invest $200, Shannon's secret is, you buy 100 shares, you have another 100 unfilled, and then all you have to do is maintain the market value of the stock and the total amount of cash.
For example, if you wait until 100 stocks hit 200, you have 200 stocks plus 100 cash, total assets 300, then you sell 50 stocks, so you have 150 stocks, 150 cash, and wait until the stock drops by one, the market value is only 75 stocks, but you have 225 total assets!
If the stock goes down and then comes back up, the result is the same, you've all made $25 right!
This sounds impossible, the stock rises twice and drops half a tonne is equal to: 2 x 0.5-1 = 0, and the price is back to where it was, but Shannon's strategy is actually making money.
The secret of Shannon's money is that he uses the Kelly formula, the most powerful forks in the universe.
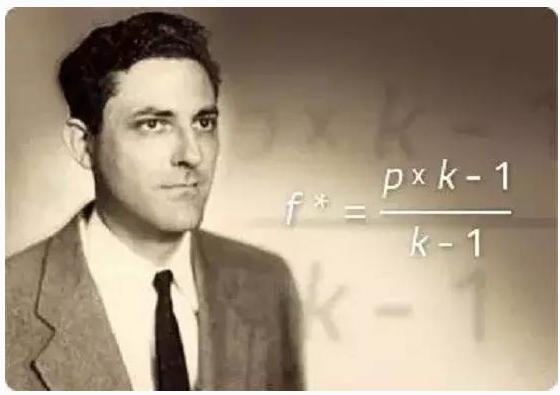
This formula was cited by Shannon's colleague Kelly at Bell Labs, who cited the investment in applications for processing communication signals based on Shannon's information theory, and Shannon's strategy was to exploit this formula.
Kelly's formula is a well-known investment formula in the investment world, known as the "Rich Fortune Formula", which deals with the question of how to calculate the optimal investment percentage in a gamble or investment based on the probability of loss.
The general formula for the Kelly equation is: f=(pb-q) /b
For example, if you throw a coin, P is the probability that you win (for example, positive), q is the probability that you lose, and in the game of coin toss, both of these values happen to be equal to 0.5, what is b? b is your winning probability, which is how much money you can win minus the money.
For example, every time you bet 1 piece, the dealer comes out and gives you 6 pieces, then this b is equal to 5 ((6 pieces minus 1 piece of your money), in which case the amount you should bet per bet is f = ((5 x 0.5-0.5) / 5 = 40%, and in this deadlock, you bet 40% of your money each time, and your future geometric return will be the maximum expected value!
In the case of the Kelley formula, no investment ratio arrangement is better than the Kelley formula!
The Kelly formula is actually very simple, for the total future value of your asset: C=(1+fb) ^Np*(1-fa) ^Nq (f: investment ratio, b winning odds, a losing odds, Np winning odds, Nq losing odds), to derive the best f from C as f, the formula is: f=p/a-q/b
This formula looks different from the previous one f=(pb-q) /b, but it's the same, if you lose and you lose all (for example, you throw a coin in the opposite direction and you lose your bet) then a is equal to 0, and when a is equal to 0, it's the same as the previous formula.
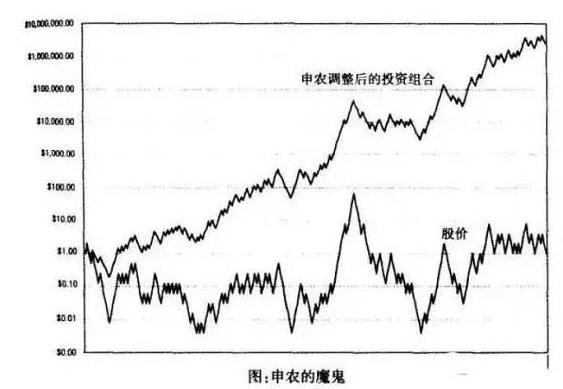
Using Kelly's formula to examine Shannon's devil again, doubling up is equivalent to you betting 1 piece, the house wins and gives you 2 pieces, and falling is half the discount, which is equivalent to you betting 1 piece, losing, the house withdraws 5 pieces. Based on this information, using Kelly's formula above, you can calculate Shannon's devil's best stake: f = p / a-q / b = 0.5⁄0.5-0.5⁄1=0.5
This is the secret of Shannon's devil, the Kelly formula calculates the optimal investment ratio is to put in half the money, which is why the principle behind each Shannon needs to be adjusted to the same market value.
If Shannon keeps playing this strategy, how much money does he make in total?
Based on the above deduction of the Kelley formula, C= ((1+0.5×1) ^ Np* ((1-0.5×0.5) ^ Nq, assuming the probability of long-term ups and downs is equal, Np = Nq = n, the result is ((1.5×0.75) ^ n = 1.125^n).
In other words, Shannon's assets will increase by 1.125 to the n-th power.
But this is counterintuitive, isn't it?
You're going up, you're going down, you're going down, you're going up, you're going down, you're going back up, you're going down, you're going to give me money?
If we look more closely, we will find a loophole: when you invest 1 buck in a bull market, you invest 1 buck in a bull market, but when you invest 1 buck in a bear market, you lose 0.5, according to the probability expectation calculation: 1 x 0.5-0.5 x 0.5 = 0.25, this impasse is clearly a positive expected return.
But if it's a game that exists and is expected to make a profit, why is it that if you own the whole stock, it's still empty in the end and you don't get a hair?
It's a very interesting phenomenon, and your bottom line has a very important relationship to your stock ratio!
You may still not get a penny in a game where you expect to make a profit.
If we measure Shannon's demon with the concept of payoff, we find that the payoff is 2×0.5=1 (2: double, 0.5: counterclockwise), which is a game that never makes a profit, and payoff never exists.
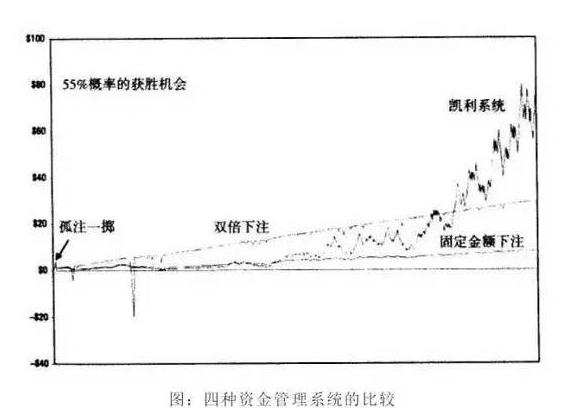
Kelly's formula is a magic formula that can make a geometric yield of zero but create infinite wealth.
If we think more deeply about Shannon's devil, we might think that the upside is zero after the downside, and that we can still make money, which is not scientific, the problem is definitely on the upside of 1 piece and the downside is only 0.5 probability.
In reality, perhaps due to the illusion that these two probabilities are not equal, the probability of a doubling down is likely to be less than half that of a fall, so the probability in the above formula is modified and you don't make any money.
Shannon's demon implies that the probabilities are equal. It makes sense to think that the two probabilities must be different, or else money would be made out of nothing.
So what we're going to look at now is whether the probability of going up twice and going down half is the same thing.
One is up 100 percent, the other is down 50 percent, and it looks completely different, obviously the number of up 100 percent is less than the number of down 50 percent.
100% and 50% are only a scale, not a probability. In terms of stock market returns, academics and practice use logarithmic returns. Although practice shows that logarithmic returns are not perfectly consistent with the normal distribution, the approximation is very high.
Before we have a better model, why don't we look at the return of the logarithm of the normal distribution first and get straight to the answer: The logarithmic yield of 100% = ln (((2⁄1) = 0.6931, the logarithmic yield of the 50% decrease = ln ((2⁄1The probability of a 100% rise and a 50% fall in the normal distribution of the logarithmic yield is the same as the probability of a 100% rise and a 50% fall in the normal distribution of the logarithmic yield.
In a situation of even probability, assuming a long-term yield of zero, you can make money with Shannon's demon, which is not strong!
So how much money can 50 cash and 50 positions in a grid trade make?
The logarithmic yield = ln (−1.1) = 0.09531, which is equal to 10% of the logarithmic yield. Now we want to calculate the logarithmic yield of the equivalent: e^ (−0.0953) = 0.909. So the probability that we're going to say 10% is going to go down is actually going to be -9.09%.
Using Kelly's formula to calculate the optimal holding ratio, then we just need to go to Shannon's devil of a stock in the future and sell some, buy some, and maintain a fixed holding ratio, and then we can achieve Shannon's devil of a profit!
So let's take the probability and the probability that we just calculated, based on the Kelly formula above: f=p/a-q/b.5⁄0.0909-0.5⁄0.1 is equal to 5.5005-5 is equal to 0.5005, which is almost equal to 0.5.
So the optimal holding ratio calculated by Kelly's formula is 50% (if you change 10% to 30%, the holding ratio becomes 200%, double the leverage).
In my introduction to Kelly's formula above, I said:
C=(1+fb)^Np(1-fa) to the nq, we're going to substitute the numbers that we just figured out: C is equal to 1 plus 0.5 times 0.1.(1-0.5×0.0909)^n=(1.05×0.95455)^n=1.0022^n
Designed according to the Kelly formula for the perfect investment ratio, a machine that makes perfect trades in a 19.09% amplitude space can earn a net profit of 0.22% per trade from the market, excluding transaction costs, assuming a normal distribution of the logarithmic returns of the stock market.
Within the rules, this rate of profit is the fastest rate of growth of account funds, which is the essential principle that grid trading can stabilize profitability by using position management under zero expectations.
In summary, grid trading is a good trading method, but there are also some disadvantages, such as fear of breaking the rules, fear of one-sidedness, etc., if you want to be comfortable using grid trading, you need to solve these disadvantages.
Some of the ideas from the network trading law:https://www.fmz.cn/bbs-topic/7567The rules of trading are detailed in the scientific principles of stable profitabilityhttps://www.fmz.cn/bbs-topic/7568Advantages and disadvantages of grid trading and strategies for optimizinghttps://www.fmz.cn/bbs-topic/7569Optimizing your trading strategy - how to choose the right investment varietieshttps://www.fmz.cn/bbs-topic/7570Optimized grid trading strategies - solving the problem of one-sided decline, reducing the network breakdown ratehttps://www.fmz.cn/bbs-topic/7571Optimization of grid trading strategies - how to use position management to quickly unlockhttps://www.fmz.cn/bbs-topic/7572Net trading is ultimately optimized - net trading yields five times higherhttps://www.fmz.cn/bbs-topic/7524The idea of a grid strategy for high-frequency brushing
- The k-line seems to have a problem.
- Please tell me how to save the data for daily voting.
- It's not fair.
- How do I get the current account, the number of coins and the current value of the coins?
- Why is the balance negative?
- Net trading is ultimately optimized - net trading yields five times higher
- Optimization of grid trading strategies - how to use position management to quickly unlock
- Optimized grid trading strategies - solving the problem of one-sided decline, reducing the network breakdown rate
- Optimizing your trading strategy - how to choose the right investment varieties
- Advantages and disadvantages of grid trading and strategies for optimizing
- A bug in the digital accuracy of the currency's disks
- How many times do you open a position for ten?
- If you want to see if there's a bull market in the review, the cycle gains and losses on the yield curve should not be visible.
- Upstream testing
- Traceback (most recent call last): File "<stdin>", line 13, in <module> File "<string>", line 23, in <module> ValueError: bad marshal data (unknown type code)
- Ask for a brushed script/code
- Please, is the accuracy of this trading variety not worth 2?Huobi/XRP_BTC
- What's the maximum length of support for k-line feedback in 1 minute?
- The problem of simulating the reassessment of the long-term contract of the yuan, the calculation of the burst
- How to brush a grid strategy to change the high-frequency brushing strategy