Quant Strategy Based on Linear Regression Intercept
Author: ChaoZhang, Date: 2023-12-29 11:45:20Tags:
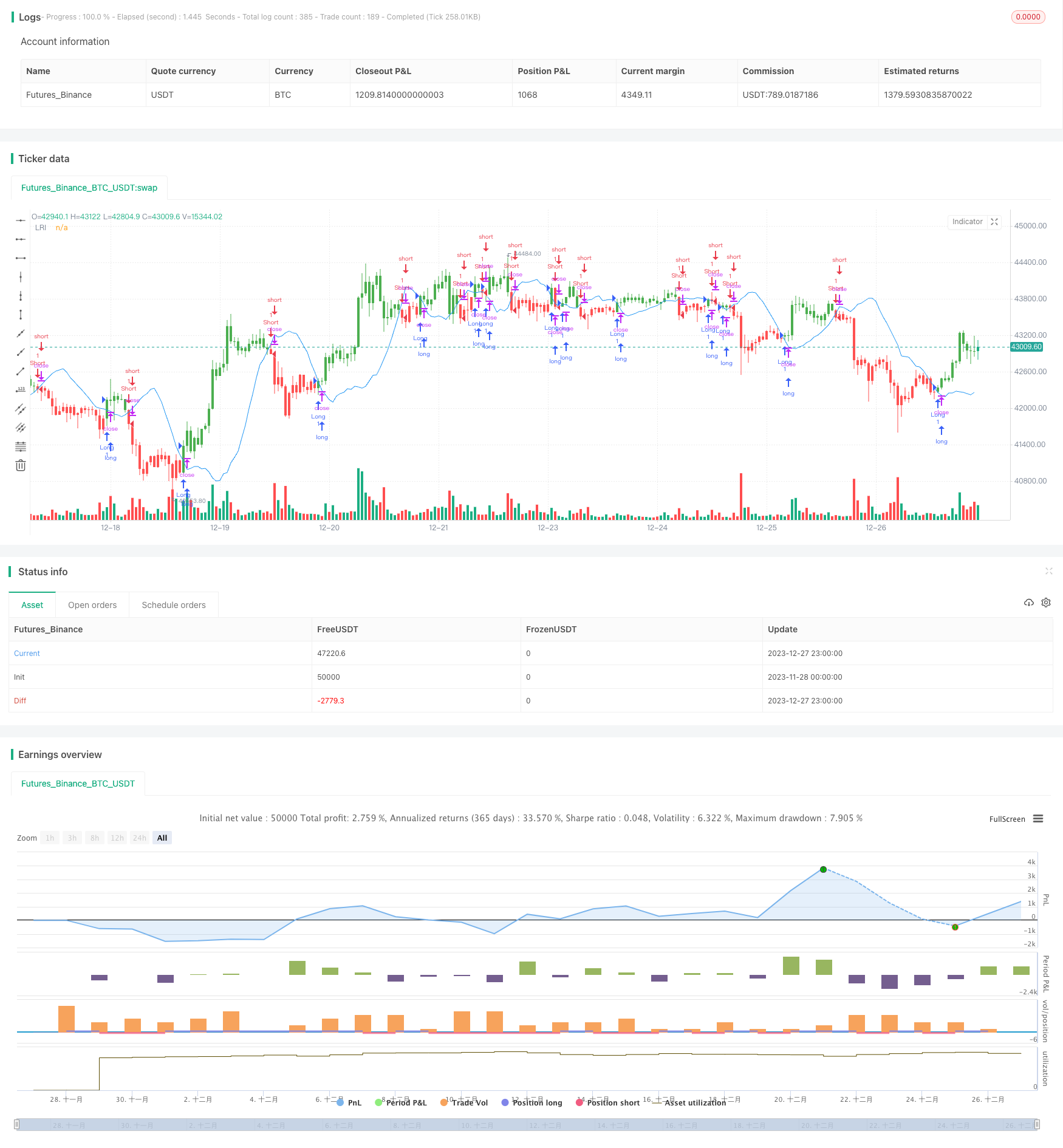
Overview
This strategy uses linear regression techniques to calculate the linear regression intercept and uses it as a trading signal to construct a quantitative trading strategy. By analyzing the price time series of stocks, this strategy fits a linear regression trend line and uses the linear regression intercept to judge whether prices are overestimated or underestimated, thereby generating trading signals.
Strategy Principle
The linear regression intercept indicates the predicted value of Y (usually the price) when the time series value X is 0. This strategy presets the parameter Length, takes the closing price as the source sequence, and calculates the linear regression intercept (xLRI) of the most recent Length days. When the closing price is higher than xLRI, go long; when the closing price is lower than xLRI, go short.
The specific calculation formula is as follows:
xX = Length *(Length - 1)* 0.5
xDivisor = xX *xX - Length* Length *(Length - 1) *(2 * Length - 1) / 6
xXY = Σ(i *Closing Price[i]), i from 0 to Length-1
xSlope = (Length *xXY - xX* Σ(Closing Price, Length))/ xDivisor
xLRI = (Σ(Closing Price, Length) - xSlope * xX) / Length
Through such calculations, the linear regression intercept xLRI for the most recent Length days can be obtained. The strategy judges the price highs and lows based on it to generate trading signals.
Advantages
This strategy has the following advantages:
- Using linear regression techniques, it has certain predictive and trend judgment capabilities for prices.
- Fewer parameters, simpler model, easy to understand and implement.
- Customizable parameter Length to adjust strategy flexibility.
Risks and Solutions
This strategy also has some risks:
- Linear regression fitting is merely a statistical fitting based on historical data, with limited ability to predict future price trends.
- If the company’s fundamentals undergo major changes, the results of linear regression fitting may become invalid.
- Improper setting of the parameter Length may lead to overfitting.
Countermeasures:
- Appropriately shorten the parameter Length to prevent overfitting.
- Pay attention to changes in the company’s fundamentals and intervene manually to close positions when necessary.
- Adopt adaptive parameter Length to dynamically adjust according to market conditions.
Optimization Directions
This strategy can also be optimized in the following aspects:
- Add a stop loss mechanism to control single loss.
- Combine with other indicators to form a combination strategy to improve stability.
- Add parameter self-adaptive optimization module to make Length parameter change dynamically.
- Add a position control module to prevent over-trading.
Summary
This strategy constructs a simple quantitative trading strategy based on the linear regression intercept. Overall, the strategy has some economic value, but there are also some risks to note. Through continuous optimization, it is expected to further improve the stability and profitability of the strategy.
/*backtest
start: 2023-11-28 00:00:00
end: 2023-12-28 00:00:00
period: 1h
basePeriod: 15m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=2
////////////////////////////////////////////////////////////
// Copyright by HPotter v1.0 21/03/2018
// Linear Regression Intercept is one of the indicators calculated by using the
// Linear Regression technique. Linear regression indicates the value of the Y
// (generally the price) when the value of X (the time series) is 0. Linear
// Regression Intercept is used along with the Linear Regression Slope to create
// the Linear Regression Line. The Linear Regression Intercept along with the Slope
// creates the Regression line.
//
// You can change long to short in the Input Settings
// WARNING:
// - For purpose educate only
// - This script to change bars colors.
////////////////////////////////////////////////////////////
strategy(title="Line Regression Intercept Backtest", overlay = true)
Length = input(14, minval=1)
xSeria = input(title="Source", defval=close)
reverse = input(false, title="Trade reverse")
xX = Length * (Length - 1) * 0.5
xDivisor = xX * xX - Length * Length * (Length - 1) * (2 * Length - 1) / 6
xXY = 0
for i = 0 to Length-1
xXY := xXY + (i * xSeria[i])
xSlope = (Length * xXY - xX * sum(xSeria, Length)) / xDivisor
xLRI = (sum(xSeria, Length) - xSlope * xX) / Length
pos = iff(close > xLRI, 1,
iff(close < xLRI, -1, nz(pos[1], 0)))
possig = iff(reverse and pos == 1, -1,
iff(reverse and pos == -1, 1, pos))
if (possig == 1)
strategy.entry("Long", strategy.long)
if (possig == -1)
strategy.entry("Short", strategy.short)
barcolor(possig == -1 ? red: possig == 1 ? green : blue )
plot(xLRI, color=blue, title="LRI")
- Dynamic Take Profit Following Trend Strategy
- 10EMA Double Cross Trend Tracking Strategy
- Dynamic Pivot Point Backtest Strategy
- Dual EMA Crossover Trend Strategy
- Anchored Rolling CVDVWAP Signal Strategy
- RSI Fibonacci Retracement Strategy
- Bollinger Bands + RSI + EMA Double Trading Strategy
- Dynamic Trailing Stop Optimization Strategy Based on Ichimoku Cloud
- High/Low Cryptocurrency Strategy Based on Multiple Indicators
- VWAP-RSI Oversold Crossunder BTC Short Strategy
- Mean Reversion Line Strategy
- Fibonacci HMA AI Buy Sell Signal Strategy
- Three Inside Down Reversal Strategy
- Quantitative Trading Dual Moving Average Strategy
- Leveraged RSI Strategy in Pine Script
- Quantitative Trading Reversal Trend Combo T3-CCI Strategy
- Dynamic Trailing Stop Loss Strategy
- Slow RSI OB/OS Strategy
- Multi-indicator Adaptive Trend Trading Strategy
- Relative Volume Price Strategy