Prueba de una estrategia de pares de inversión de la media intradiaria entre SPY e IWM

En este artículo vamos a considerar nuestra primera estrategia de negociación intradiaria. Usará una idea de negociación clásica, la de pares de negociación. En este caso vamos a hacer uso de dos fondos negociados en bolsa (ETF), SPY e IWM, que se negocian en la Bolsa de Valores de Nueva York (NYSE) e intentan representar los índices del mercado de valores de los Estados Unidos, el S&P500 y el Russell 2000, respectivamente.

La estrategia generalmente crea un spread entre el par de ETFs al anhelar uno y a cortocircuitar una cantidad del otro. La proporción de largo a corto puede definirse de muchas maneras, como utilizando técnicas de series de tiempo de cointegración estadística. En este escenario vamos a calcular una proporción de cobertura entre SPY e IWM a través de una regresión lineal rodante. Esto luego nos permitirá crear un spread entre SPY e IWM que se normaliza a un puntaje z. Las señales comerciales se generarán cuando el puntaje z exceda ciertos umbrales bajo la creencia de que el spread volverá a la media.

La lógica de la estrategia es que SPY e IWM caracterizan aproximadamente la misma situación, la de la economía de un grupo de corporaciones estadounidenses de gran capitalización y de pequeña capitalización. La premisa es que si uno toma el diferencial de los precios, entonces debería ser la inversión media, ya que mientras que los eventos local (en el tiempo) pueden afectar los índices S&P500 o Russell 2000 por separado (como diferencias de pequeña capitalización / gran capitalización, fechas de reequilibrio o operaciones en bloque), es probable que las series de precios a largo plazo de los dos se cointegren.

La estrategia

La estrategia se lleva a cabo en las siguientes fases:

1. Los datos - barras de 1 minuto de SPY e IWM se obtienen desde abril de 2007 hasta febrero de 2014.
2. Procesamiento: los datos se alinean correctamente y las barras faltantes se descartan mutuamente.
3. Spread - La relación de cobertura entre los dos ETFs se calcula tomando una regresión lineal en movimiento. Esto se define como el coeficiente de regresión β utilizando una ventana de retroceso que se desplaza hacia adelante en 1 bar y recalcula los coeficientes de regresión. Por lo tanto, la relación de cobertura βi, para bar bi se calcula a través de los puntos bi−1−k a bi−1 para una retroceso de k bares.
4. Z-Score - La puntuación estándar del spread se calcula de la manera habitual. Esto significa restar la media (muestra) del spread y dividir por la desviación estándar (muestra) del spread. La razón de esto es hacer que los parámetros de umbral sean más sencillos de interpretar ya que el z-score es una cantidad sin dimensiones. He introducido deliberadamente un sesgo de lookahead en los cálculos para mostrar lo sutil que puede ser.
5. Las operaciones - Las señales largas se generan cuando el puntaje negativo de z cae por debajo de un umbral predeterminado (o post-optimizado), mientras que las señales cortas son lo contrario. Las señales de salida se generan cuando el puntaje absoluto de z cae por debajo de un umbral adicional. Para esta estrategia he elegido (algo arbitrariamente) un umbral de entrada absoluto de 10.000z=2 y un umbral de salida de 10.000z=1.

Tal vez la mejor manera de entender la estrategia en profundidad es implementarla. La siguiente sección describe un código completo de Python (archivo único) para implementar esta estrategia de reversión de la media. He comentado libremente el código para ayudar a la comprensión.

Implementación de Python

Al igual que con todos los tutoriales de Python / pandas, es necesario tener configurado un entorno de investigación de Python como se describe en este tutorial. Una vez configurado, la primera tarea es importar las bibliotecas de Python necesarias. Para esta prueba posterior se requieren matplotlib y pandas.

Las versiones específicas de la biblioteca que estoy usando son las siguientes:

• Python - 2.7.3
• NumPy - 1.8.0
• Los pandas - 0.12.0
• - el número de personas que han sido objeto de una investigación Vamos a importar las bibliotecas:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

La siguiente función create_pairs_dataframe importa dos archivos CSV que contienen las barras intradiarias de dos símbolos. En nuestro caso serán SPY e IWM. Luego crea un par de marcos de datos separado, que utiliza los índices de ambos archivos originales. Dado que sus marcas de tiempo probablemente sean diferentes debido a operaciones y errores perdidos, esto garantiza que tendremos datos coincidentes. Este es uno de los principales beneficios de usar una biblioteca de análisis de datos como pandas.

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

El siguiente paso es llevar a cabo la regresión lineal rodante entre SPY e IWM. En este caso IWM es el predictor (x) y SPY es la respuesta (y). He establecido una ventana de retroceso predeterminada de 100 barras. Como se discutió anteriormente, este es un parámetro de la estrategia. Para que la estrategia sea considerada robusta, lo ideal es ver un perfil de retornos (u otra medida de rendimiento) como una función convexa del período de retroceso. Por lo tanto, en una etapa posterior del código llevaremos a cabo un análisis de sensibilidad variando el período de retroceso en un rango.

Una vez que se calcula el coeficiente de beta rodante en el modelo de regresión lineal para SPY-IWM, lo agregamos a los pares DataFrame y eliminamos las filas vacías. Esto constituye el primer conjunto de barras iguales al tamaño de la vista como medida de recorte. Luego creamos la propagación de los dos ETF como una unidad de unidades SPY y −βi de IWM. Claramente esta no es una situación realista ya que estamos tomando cantidades fraccionarias de IWM, lo que no es posible en una implementación real.

Finalmente, creamos la puntuación z de la propagación, que se calcula restando la media de la propagación y normalizando por la desviación estándar de la propagación. Tenga en cuenta que hay un sesgo de la cabeza de mirador bastante sutil que ocurre aquí. Lo dejé deliberadamente en el código porque quería enfatizar lo fácil que es cometer tal error en la investigación. La media y la desviación estándar se calculan para toda la serie de tiempo de propagación. Si esto es para reflejar la verdadera precisión histórica, entonces esta información no habría estado disponible ya que implícitamente utiliza información futura. Por lo tanto, debemos usar una media de rodaje y stdev para calcular la puntuación z.

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

En create_long_short_market_signals se crean las señales comerciales. Estas se calculan al ir largo el spread cuando el z-score excede negativamente un z-score negativo y al ir corto el spread cuando el z-score excede positivamente un z-score positivo. La señal de salida se da cuando el valor absoluto del z-score es menor o igual a otro umbral (menor en magnitud).

Para lograr esta situación, es necesario saber, para cada barra, si la estrategia es in o out del mercado. long_market y short_market son dos variables definidas para realizar un seguimiento de las posiciones largas y cortas del mercado. Desafortunadamente, esto es mucho más simple de codificar de manera iterativa en lugar de un enfoque vectorizado y, por lo tanto, es lento de calcular. A pesar de las barras de 1 minuto que requieren ~ 700,000 puntos de datos por archivo CSV, todavía es relativamente rápido de calcular en mi máquina de escritorio más antigua!

Para iterar sobre un DataFrame panda (que, sin duda, NO es una operación común) es necesario utilizar el método iterrows, que proporciona un generador sobre el que iterar:

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

En esta etapa, hemos actualizado los pares para contener las señales reales largo / corto, lo que nos permite determinar si necesitamos estar en el mercado. Ahora necesitamos crear una cartera para realizar un seguimiento del valor de mercado de las posiciones. La primera tarea es crear una columna de posiciones que combina las señales largas y cortas. Esto contendrá una lista de elementos de (1,0,−1), con 1 que representa una posición larga / mercado, 0 que representa ninguna posición (debería salir) y -1 que representa una posición corta / mercado. Las columnas sym1 y sym2 representan los valores de mercado de las posiciones SPY e IWM al cierre de cada barra.

Una vez que se han creado los valores de mercado del ETF, los sumamos para producir un valor total de mercado al final de cada barra. Esto se convierte luego en un flujo de retornos por el método pct_change para ese objeto Serie. Las líneas posteriores de código eliminan las entradas malas (elementos NaN e inf) y finalmente calculan la curva de equidad completa.

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Elel principalLos archivos CSV intradiarios se encuentran en la ruta datadir. Asegúrese de modificar el código a continuación para apuntar a su directorio particular.

Para determinar qué tan sensible es la estrategia al período de retroceso, es necesario calcular una métrica de rendimiento para un rango de retrocesos. He elegido el rendimiento porcentual total final de la cartera como medida de rendimiento y el rango de retroceso en [50,200] con incrementos de 10.

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

El gráfico del período de retroceso frente a los retornos ahora se puede ver. Nótese que hay un máximo 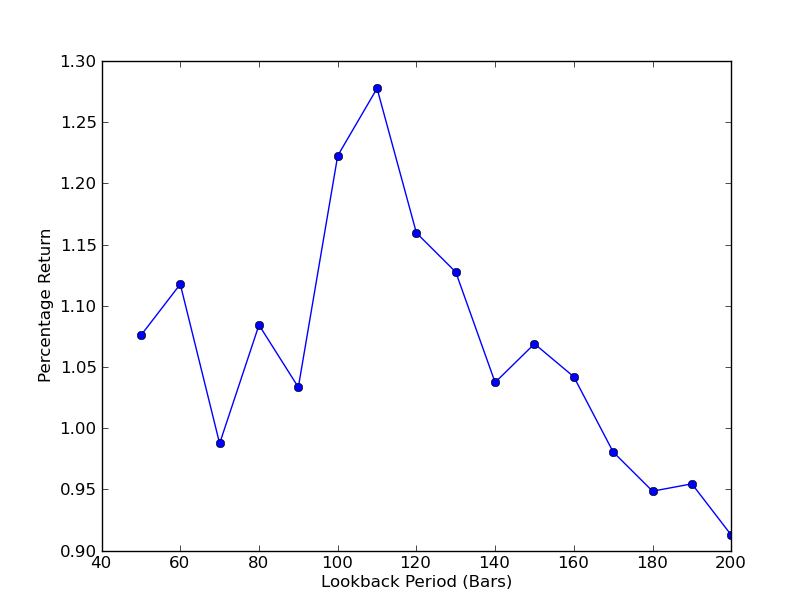global alrededor de un retroceso igual a 110 bares. Si hubiéramos visto una situación en la que el retroceso era independiente de los retornos, esto habría sido motivo de preocupación:Análisis de la sensibilidad del período de retroalimentación del coeficiente de cobertura de regresión lineal SPY-IWM

Ningún artículo de backtesting estaría completo sin una curva de equidad con pendiente ascendente! Por lo tanto, si desea trazar una curva de los rendimientos acumulados frente al tiempo, puede usar el siguiente código. Trazará la cartera final generada a partir del estudio de parámetros de retroceso. Por lo tanto, será necesario elegir el retroceso dependiendo del gráfico que desee visualizar. El gráfico también traza los rendimientos de SPY en el mismo período para facilitar la comparación:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

El siguiente gráfico de la curva de renta variable es para un período de observación de 100 días: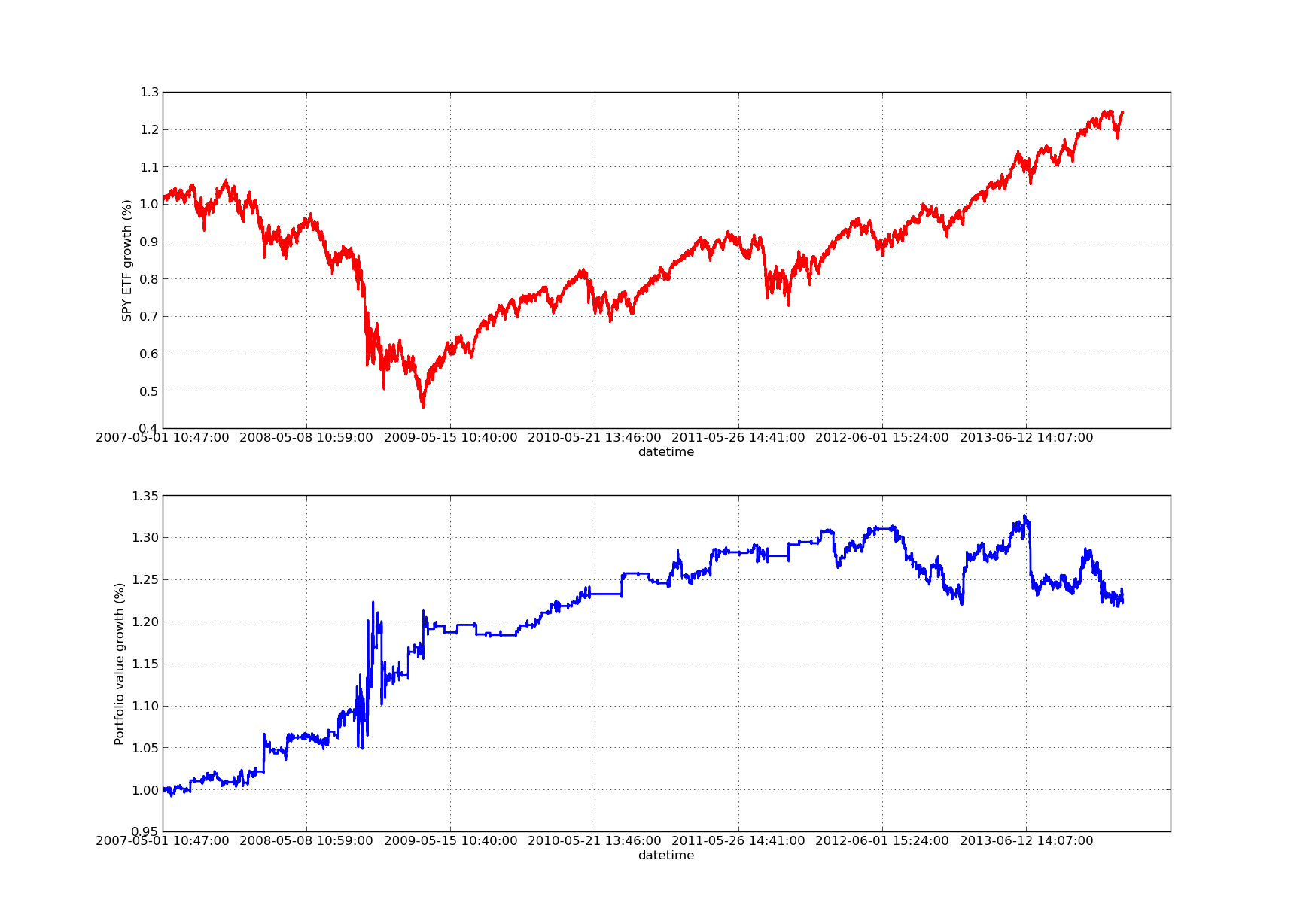Análisis de la sensibilidad del período de retroalimentación del coeficiente de cobertura de regresión lineal SPY-IWM

Se debe tener en cuenta que la reducción de SPY es significativa en 2009 durante el período de la crisis financiera. La estrategia también tuvo un período volátil en esta etapa. También hay que tener en cuenta que el rendimiento se ha deteriorado algo en el último año debido a la fuerte tendencia de SPY en este período, que refleja el índice S&P500.

Tenga en cuenta que todavía tenemos que tener en cuenta el sesgo de la mirada al calcular la puntuación z del spread. Además, todos estos cálculos se han llevado a cabo sin costos de transacción. Esta estrategia ciertamente funcionaría muy mal una vez que se toman en cuenta estos factores. Las tarifas, el spread bid / ask y el deslizamiento no se tienen en cuenta actualmente. Además, la estrategia se negocia en unidades fraccionarias de ETF, lo que también es muy poco realista.

En artículos posteriores crearemos un backtester mucho más sofisticado basado en eventos que tomará estos factores en consideración y nos dará una confianza significativamente mayor en nuestra curva de equidad y métricas de rendimiento.