Una estrategia de negociación intradía que utiliza la regresión de la media entre SPY e IWM

En este artículo, vamos a redactar una estrategia de intradía. Usará la idea clásica de la negociación, que es el par de transacciones de retorno a la paridad. En este ejemplo, vamos a utilizar dos fondos de índices abiertos (ETF), SPY e IWM, que se negocian en la Bolsa de Nueva York (NYSE) e intentan representar los índices de las bolsas estadounidenses, respectivamente, el S&P 500 y el Russell 2000.

La estrategia consiste en crear una diferencia de ganancias al hacer más de un ETF y hacer un ETF vacío. La diferencia de ganancias puede definirse de muchas maneras, por ejemplo, utilizando un método de secuencias de tiempo de consonancia estadística. En este escenario, calcularemos la relación de cobertura entre SPY e IWM mediante una regresión lineal giratoria. Esto nos permitirá crear una diferencia de ganancias entre SPY e IWM, que se estandarizará como un z-score. Cuando el z-score exceda un cierto umbral, se generará una señal de negociación, ya que creemos que la diferencia de ganancias se restablecerá a la media.

El principio básico de esta estrategia es que SPY e IWM representan aproximadamente la misma situación del mercado, es decir, el desempeño de las acciones de un grupo de compañías estadounidenses grandes y pequeñas. La premisa es que siempre hay regreso si se acepta la teoría de la retracción de la paridad de la paridad de precios, ya que las paridades de eventos de paridad pueden afectar al S&P 500 y al Russell 2000 respectivamente en un corto período de tiempo, pero la diferencia de ganancias entre ellos siempre vuelve a la media normal, y las dos series de precios a largo plazo siempre están integradas.

La estrategia

La estrategia se ejecuta en los siguientes pasos:

Datos - desde abril de 2007 hasta febrero de 2014, se obtuvieron gráficos de k minutos de SPY e IWM respectivamente.

Procesamiento - Alinea los datos correctamente y elimina las k-strings que faltan una a la otra.

Diferencia - La relación de cobertura entre los dos ETFs utiliza un cálculo de regresión lineal giratoria. Se define como el coeficiente de regresión β utilizando una ventana retrograda que mueve hacia adelante la línea k de 1 raíz y recalcula el coeficiente de regresión. Por lo tanto, la relación de cobertura βi, la línea bi-raíz K es utilizada para retroceder la línea k mediante el cálculo del punto de cruce de bi-1-k a bi-1, para la cual se utiliza el coeficiente de cobertura.

Z-Score - El valor de la diferencia estándar se calcula de la manera habitual. Esto significa que se deduce el valor medio de la diferencia estándar de la muestra y se exime de la diferencia estándar de la muestra. La razón para hacerlo es para que los parámetros de umbral sean más fáciles de entender, ya que la Z-Score es una cantidad sin dimensiones.

Negociación - Cuando el valor del z-score negativo cae por debajo del límite previsto (o post-optimizado), se produce una señal de hacer más, mientras que la señal de hacer nada es el contrario. Cuando el valor absoluto del z-score cae por debajo del límite adicional, se generará una señal de equilibrio. Para esta estrategia, elegí (algo al azar) el z-score = 2 como el límite de apertura y el z-score = 1 como el límite de equilibrio.

Tal vez la mejor manera de profundizar en la comprensión de la política es implementarla en la práctica. La siguiente sección describe en detalle el código completo de Python para implementar esta política de retorno de valores iguales (un solo archivo). He agregado una nota de código detallada para ayudarlo a comprender mejor.

Implementación de Python

Como todos los tutoriales de Python/pandas, se debe configurar de acuerdo con el entorno Python descrito en este tutorial. Una vez que la configuración está completa, la primera tarea es importar la biblioteca Python necesaria. Esto es necesario para usar matplotlib y pandas.

Las versiones específicas que utilizo son las siguientes:

Python - 2.7.3 NumPy - 1.8.0 Los pandas - 0.12.0 - el número de personas que han sido objeto de una investigación

En el caso de las bibliotecas de Internet, las bibliotecas de Internet son las más utilizadas.

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

La siguiente función create_pairs_dataframe importa dos ficheros CSV de k líneas internas que contienen dos símbolos. En nuestro ejemplo, esto sería SPY e IWM. Luego crea un par de pares de pares de pares de pares de datos separados, que utilizarán los índices de los dos archivos originales.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

El siguiente paso es realizar una regresión lineal de rotación entre SPY e IWM. En este escenario, IWM es el predictor (x) y SPY es la respuesta (y). Configuro una ventana de retroceso predeterminada de 100 k-líneas. Como se mencionó anteriormente, estos son los parámetros de la política. Para que la política sea considerada sólida, idealmente queremos ver un informe de retorno que muestre el estado de la función convexa (x) u otras medidas de rendimiento en la regresión. Por lo tanto, en la etapa posterior del código, haremos un análisis de sensibilidad mediante períodos de retroceso dentro del rango de cambios.

Después de calcular el coeficiente de rotación β en el modelo de regresión lineal SPY-IWM, añadirlo al DataFrame y eliminar las líneas en blanco. Esto construye el primer grupo de líneas K, que es igual a la medida de corte de longitud retrograda. Luego, creamos dos diferencias de ETF, unidades de SPY y unidades de -βi de IWM respectivamente. Obviamente, esto no es un caso realista, ya que estamos adoptando una pequeña cantidad de IWM, lo que no es posible en la implementación real.

Finalmente, creamos un z-score de la diferencia de interés, que se calcula restando el promedio de la diferencia de interés y utilizando el estándar de diferencia de interés. Hay que tener en cuenta que aquí existe un par de parámetros de desviación prospectiva bastante delicados. Lo dejé en el código deliberadamente porque quería enfatizar lo fácil que es cometer errores en el estudio.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

En create_long_short_market_signals, se crean señales comerciales. Estas son calculadas por el valor de la puntuación z superior al umbral. Se da una señal de equilibrio cuando el valor absoluto de la puntuación z es menor o igual a otro umbral.

Para lograr esto, es necesario establecer una estrategia de negociación para cada k-string, que sea un depósito abierto o un depósito abierto. Long_market y short_market son las dos variables definidas para rastrear las posiciones de multi-head y empty-head. Desafortunadamente, es más fácil de programar en forma iterativa que el método de cuantificación, por lo que se calcula lentamente. Aunque los gráficos de k-string de 1 minuto requieren alrededor de 700,000 puntos de datos por archivo CSV, en mi viejo escritorio todavía se calcula relativamente rápido!

Para iterar un DataFrame pandas (que sin duda es una operación poco común) es necesario utilizar el método iterrows, que proporciona un generador iterativo:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

En esta etapa, hemos actualizado los pares para incluir señales reales múltiples y vacías, lo que nos permite determinar si necesitamos abrir una posición. Ahora necesitamos crear una cartera para rastrear el valor del mercado de las posiciones. La primera tarea es crear una columna de posiciones que combine señales múltiples y señales vacías.

Una vez que se crea el valor de mercado del ETF, los combinamos para producir el valor de mercado total al final de cada línea k. Luego lo convertimos a un valor de retorno a través del método pct_change del objeto. Las siguientes líneas de código eliminan las entradas incorrectas (los elementos NaN e inf) y finalmente se calcula la curva de intereses completa.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Las funciones principales las combinan. Los archivos CSV se encuentran en el camino datadir. Asegúrese de modificar el código siguiente para apuntar a su directorio específico.

Para determinar la sensibilidad de la estrategia a los ciclos de lookback, es necesario calcular una serie de indicadores de rendimiento de lookback. He elegido el porcentaje de retorno total final de la cartera como indicador de rendimiento y el rango de lookback[50,200], con un incremento de 10.

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

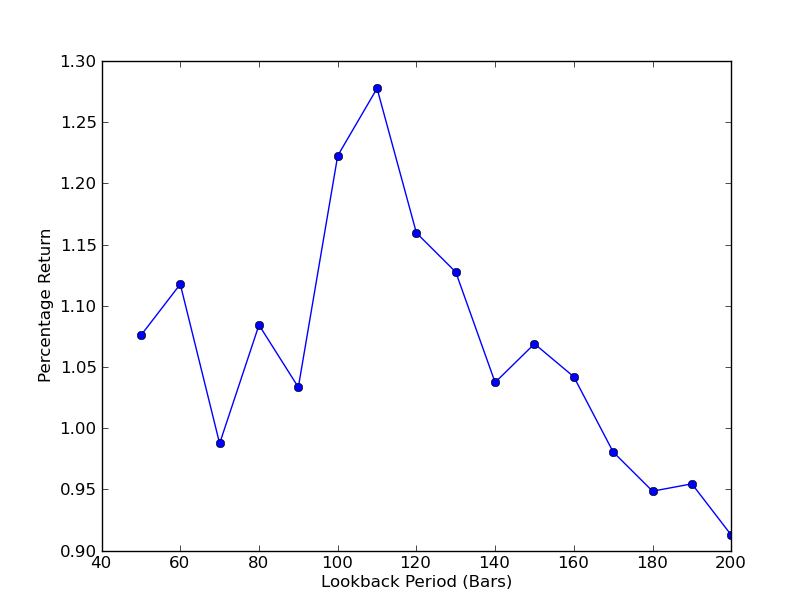
Ahora se puede ver un gráfico de lookbacks y retornos. Tenga en cuenta que lookback tiene un valor máximo de lookbacks global, que es igual a 110 k. Si vemos que los lookbacks no están relacionados con los retornos, es porque:

Análisis de la sensibilidad del período de retroceso de la cobertura de regresión lineal SPY-IWM

Sin una curva de ganancias inclinada hacia arriba, cualquier artículo de retrospectiva es incompleto. Por lo tanto, si desea trazar una curva de rendimiento acumulativo de ganancias con el tiempo, puede utilizar el siguiente código. Trazará la cartera final generada a partir del estudio de los parámetros de lookback. Por lo tanto, es necesario seleccionar lookback según el gráfico que desea visualizar.

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

El siguiente gráfico de la curva de intereses tiene un período de observación de 100 días:

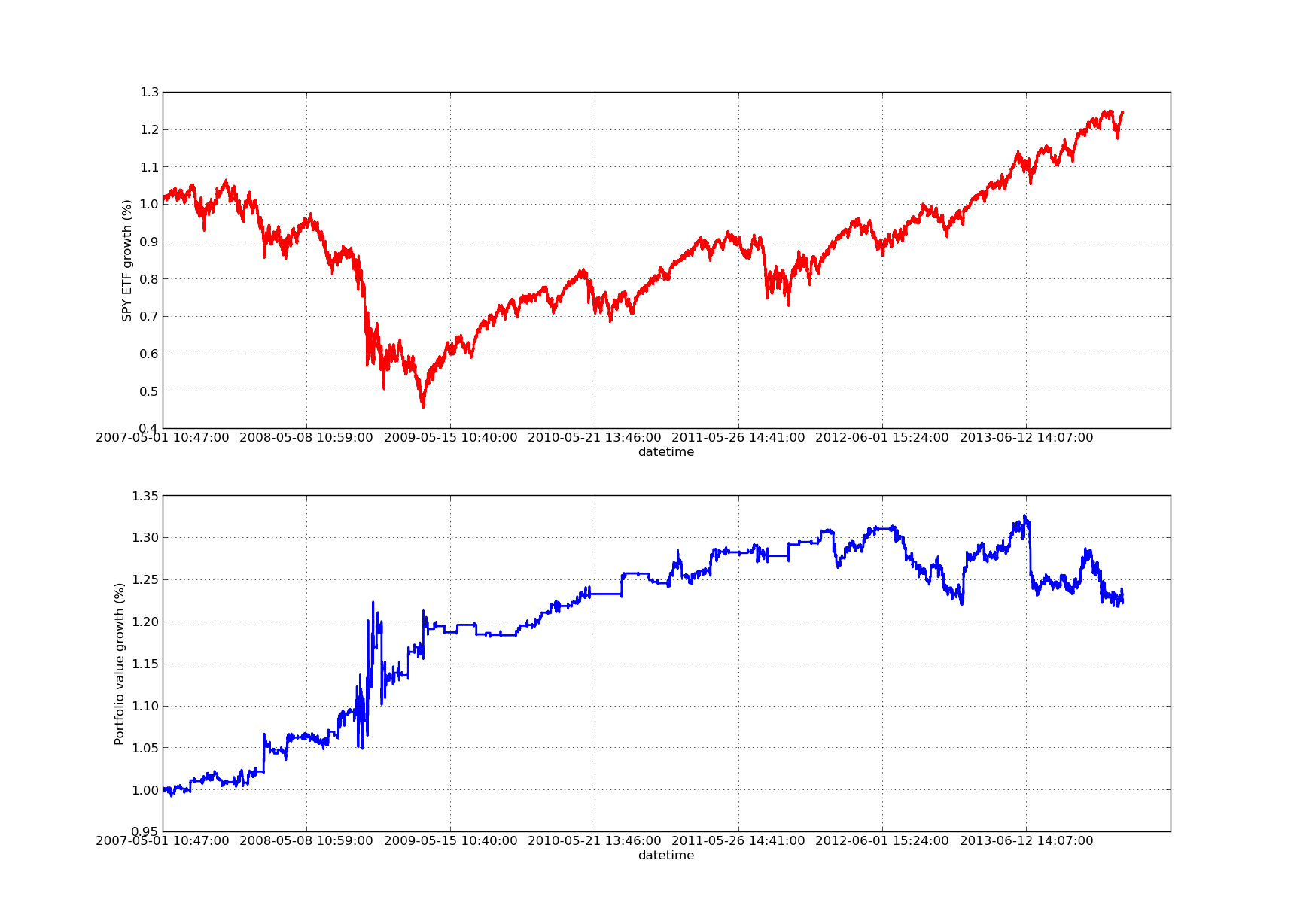
Análisis de la sensibilidad del período de retroceso de la cobertura de regresión lineal SPY-IWM

Tenga en cuenta que durante la crisis financiera, el SPY 2009 se contrajo considerablemente. La estrategia también se encontraba en un período de turbulencia en esta etapa. Tenga en cuenta que el rendimiento del año pasado se deterioró debido a la fuerte naturaleza de tendencia del SPY durante este período, lo que refleja el índice S&P 500.

Tenga en cuenta que, al calcular la diferencia de interés de la puntuación z, todavía necesitamos tener en cuenta el parámetro de desviación prospectiva. Además, todos estos cálculos se realizaron sin costos de transacción. Una vez que se tienen en cuenta estos factores, esta estrategia seguramente funcionará mal. Las tarifas y los puntos de deslizamiento no están definidos actualmente. Además, la estrategia es para operar con un número mínimo de unidades del ETF, lo cual también es muy poco realista.

En un artículo más adelante, crearemos un backtester más complejo impulsado por eventos que tendrá en cuenta todos estos factores, lo que nos dará más confianza en la curva de capital y los indicadores de rendimiento.