Estrategia cuántica basada en la interceptación de regresión lineal

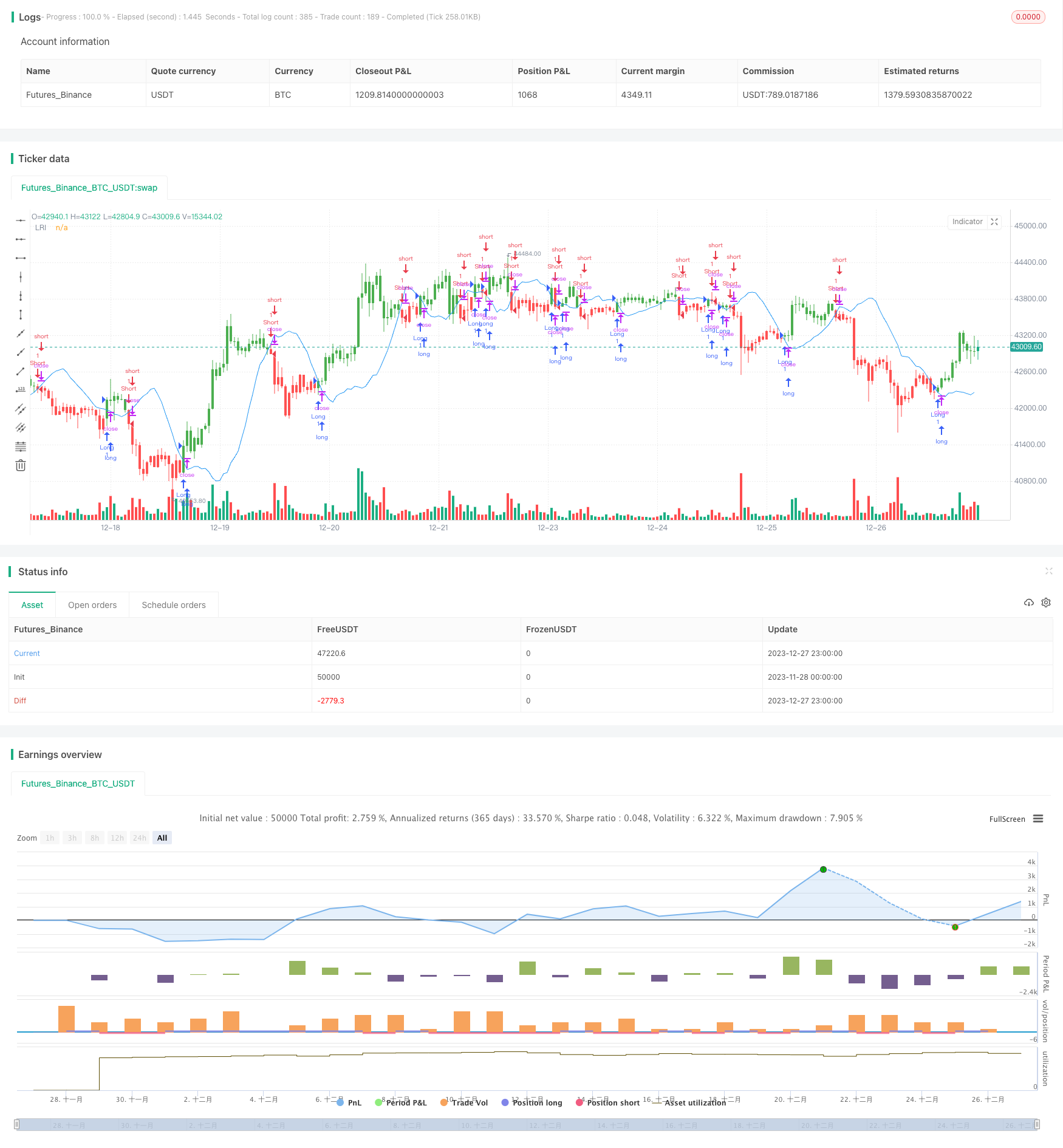
Resumen general

Esta estrategia utiliza técnicas de regresión lineal para calcular la intercepción de regresión lineal y la utiliza como señal de negociación para construir una estrategia de negociación cuantitativa. Al analizar las series de tiempo de precios de las acciones, esta estrategia se ajusta a una línea de tendencia de regresión lineal y utiliza la intercepción de regresión lineal para juzgar si los precios están sobreestimados o subestimados, generando así señales de negociación.

Principio de la estrategia

La intersección de regresión lineal indica el valor predicho de Y (generalmente el precio) cuando el valor de la serie de tiempo X es 0. Esta estrategia prefiere el parámetro Length, toma el precio de cierre como la secuencia de origen y calcula la intersección de regresión lineal (xLRI) de los días de longitud más recientes.

La fórmula específica de cálculo es la siguiente:

xX = Length *(Length - 1)* 0.5
xDivisor = xX *xX - Length* Length *(Length - 1) *(2 * Length - 1) / 6  
xXY = Σ(i *Closing Price[i]), i from 0 to Length-1
xSlope = (Length *xXY - xX* Σ(Closing Price, Length))/ xDivisor 
xLRI = (Σ(Closing Price, Length) - xSlope * xX) / Length

A través de dichos cálculos, se puede obtener la interceptación de regresión lineal xLRI para los días de longitud más recientes.

Ventajas

Esta estrategia tiene las siguientes ventajas:

1. Utilizando técnicas de regresión lineal, tiene ciertas capacidades predictivas y de juicio de tendencias para los precios.
2. Menos parámetros, modelo más simple, fácil de entender e implementar.
3. Parámetro personalizable longitud para ajustar la flexibilidad de la estrategia.

Riesgos y soluciones

Esta estrategia también tiene algunos riesgos:

1. El ajuste de regresión lineal es simplemente un ajuste estadístico basado en datos históricos, con una capacidad limitada para predecir las tendencias futuras de los precios.
2. Si los fundamentos de la empresa sufren cambios importantes, los resultados del ajuste de regresión lineal pueden volverse inválidos.
3. El ajuste incorrecto del parámetro Length puede dar lugar a un sobreajuste.

Contramedidas:

1. Reducir adecuadamente el parámetro longitud para evitar el sobreajuste.
2. Preste atención a los cambios en los fundamentos de la empresa e intervenga manualmente para cerrar posiciones cuando sea necesario.
3. Adoptar el parámetro adaptativo longitud para ajustar dinámicamente de acuerdo con las condiciones del mercado.

Direcciones de optimización

Esta estrategia también puede optimizarse en los siguientes aspectos:

1. Añadir un mecanismo de stop loss para controlar pérdidas individuales.
2. Combinar con otros indicadores para formar una estrategia combinada para mejorar la estabilidad.
3. Añadir el módulo de optimización autoadaptable de parámetros para hacer que el parámetro de longitud cambie dinámicamente.
4. Añadir un módulo de control de posición para evitar el exceso de negociación.

Resumen de las actividades

Esta estrategia construye una estrategia comercial cuantitativa simple basada en la intercepción de regresión lineal. En general, la estrategia tiene cierto valor económico, pero también hay algunos riesgos a tener en cuenta.