Retour en arrière sur une stratégie de paires d'inversion de la moyenne intraday entre SPY et IWM

Dans cet article, nous allons examiner notre première stratégie de trading intraday. Elle utilisera une idée de trading classique, celle des paires de trading. Dans ce cas, nous allons utiliser deux fonds négociés en bourse (ETF), SPY et IWM, qui sont négociés à la Bourse de New York (NYSE) et tentent de représenter les indices boursiers américains, le S&P500 et le Russell 2000, respectivement.

La stratégie crée généralement un spread entre la paire d'ETF en longant l'un et en raccourcissant une quantité de l'autre. Le rapport long à court peut être défini de plusieurs façons, telles que l'utilisation de techniques de séries temporelles de cointégration statistique. Dans ce scénario, nous allons calculer un ratio de couverture entre SPY et IWM via une régression linéaire en roulement. Cela nous permettra ensuite de créer un spread entre SPY et IWM qui est normalisé à un score z. Les signaux de trading seront générés lorsque le score z dépasse certains seuils dans la croyance que l'écart reviendra à la moyenne.

La logique de la stratégie est que SPY et IWM caractérisent approximativement la même situation, celle de l'économie d'un groupe de sociétés américaines à grande capitalisation et à petite capitalisation.

La stratégie

La stratégie est mise en œuvre dans les étapes suivantes:

1. Les données - barres de SPY et IWM de 1 minute sont obtenues d'avril 2007 à février 2014.
2. Traitement - Les données sont correctement alignées et les barres manquantes sont mutuellement écartées.
3. Diffusion - Le ratio de couverture entre les deux ETF est calculé en prenant une régression linéaire en roulement. Ceci est défini comme le coefficient de régression β en utilisant une fenêtre de rétrospective qui avance de 1 bar et recalcule les coefficients de régression. Ainsi, le ratio de couverture βi, pour bar bi est calculé à travers les points bi−1−k à bi−1 pour un rétrospectif de k bar.
4. Z-Score - Le score standard de l'écart est calculé de la manière habituelle. Cela signifie soustraire la moyenne (échantillon) de l'écart et diviser par l'écart type (échantillon) de l'écart. La raison de cela est de rendre les paramètres de seuil plus simples à interpréter puisque le score z est une quantité sans dimension. J'ai délibérément introduit un biais de lookhead dans les calculs afin de montrer à quel point il peut être subtil. Essayez et faites attention!
5. Les signaux longs sont générés lorsque le score z négatif tombe en dessous d'un seuil prédéterminé (ou post-optimisé), tandis que les signaux courts en sont l'inverse. Les signaux de sortie sont générés lorsque le score z absolu tombe en dessous d'un seuil supplémentaire. Pour cette stratégie, j'ai (un peu arbitrairement) choisi un seuil d'entrée absolu de 10000z=2 et un seuil de sortie de 10000z=1.

Peut-être que la meilleure façon de comprendre la stratégie en profondeur est de l'implémenter réellement. La section suivante décrit un code Python complet (fichier unique) pour la mise en œuvre de cette stratégie de renversement de la moyenne. J'ai libéralement commenté le code afin d'aider à la compréhension.

Mise en œuvre de Python

Comme pour tous les tutoriels Python / pandas, il est nécessaire d'avoir un environnement de recherche Python comme décrit dans ce tutoriel. Une fois configuré, la première tâche consiste à importer les bibliothèques Python nécessaires.

Les versions spécifiques de bibliothèque que j'utilise sont les suivantes:

• Python - 2.7.3
• NumPy - 1.8.0
• Les pandas - 0.12.0
• Le projet de loi Allons importer les bibliothèques:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

La fonction suivante create_pairs_dataframe importe deux fichiers CSV contenant les barres intraday de deux symboles. Dans notre cas, ce sera SPY et IWM. Elle crée ensuite des paires de données séparées, qui utilisent les index des deux fichiers d'origine. Puisque leurs horodatages sont susceptibles d'être différents en raison de transactions manquées et d'erreurs, cela garantit que nous aurons des données correspondantes. C'est l'un des principaux avantages de l'utilisation d'une bibliothèque d'analyse de données comme panda. Le code boilerplate est géré pour nous de manière très efficace.

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

L'étape suivante consiste à effectuer la régression linéaire en roulement entre SPY et IWM. Dans ce cas, IWM est le prédicteur (x) et SPY est la réponse (y). J'ai défini une fenêtre de rétrospection par défaut de 100 barres. Comme indiqué ci-dessus, il s'agit d'un paramètre de la stratégie. Pour que la stratégie soit considérée comme robuste, nous voulons idéalement voir un profil de rendement (ou une autre mesure de performance) comme une fonction convexe de la période de rétrospection. Ainsi, à un stade ultérieur du code, nous effectuerons une analyse de sensibilité en variant la période de rétrospection sur une plage.

Une fois que le coefficient bêta en rotation est calculé dans le modèle de régression linéaire pour SPY-IWM, nous l'ajoutons aux paires DataFrame et supprimons les lignes vides. Cela constitue le premier ensemble de barres égal à la taille du lookback comme mesure de découpage. Nous créons ensuite l'écartement des deux ETF en unité de SPY et −βi unités de IWM.

Enfin, nous créons le z-score de l'écart, qui est calculé en soustrayant la moyenne de l'écart et en normalisant par l'écart-type de l'écart. Notez qu'il y a un biais plutôt subtil. Je l'ai délibérément laissé dans le code car je voulais souligner à quel point il est facile de faire une telle erreur dans la recherche. La moyenne et l'écart-type sont calculés pour l'ensemble de la série temporelle d'écart. Si cela reflète une véritable précision historique, alors cette information n'aurait pas été disponible car elle utilise implicitement des informations futures. Nous devrions donc utiliser une moyenne mobile et stdev pour calculer l'écart-type.

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Dans create_long_short_market_signals, les signaux de trading sont créés. Ils sont calculés en allant long le spread lorsque le z-score dépasse négativement un z-score négatif et en allant court le spread lorsque le z-score dépasse positivement un z-score positif. Le signal de sortie est donné lorsque la valeur absolue du z-score est inférieure ou égale à un autre seuil (plus petit en grandeur).

Pour atteindre cette situation, il est nécessaire de savoir, pour chaque barre, si la stratégie est in ou out du marché. long_market et short_market sont deux variables définies pour garder une trace des positions longues et courtes du marché. Malheureusement, cela est beaucoup plus simple à coder de manière itérative par opposition à une approche vectorialisée et il est donc lent à calculer.

Pour itérer sur un Panda DataFrame (ce qui n'est certes PAS une opération courante), il est nécessaire d'utiliser la méthode iterrows, qui fournit un générateur sur lequel itérer:

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

À ce stade, nous avons mis à jour les paires pour contenir les signaux longs / courts réels, ce qui nous permet de déterminer si nous devons être sur le marché. Maintenant, nous devons créer un portefeuille pour garder une trace de la valeur marchande des positions. La première tâche consiste à créer une colonne de positions qui combine les signaux longs et courts. Cela contiendra une liste d'éléments de (1,0,−1), avec 1 représentant une position longue / marché, 0 représentant aucune position (doit être quitté) et -1 représentant une position courte / marché. Les colonnes sym1 et sym2 représentent les valeurs de marché des positions SPY et IWM à la clôture de chaque barre.

Une fois que les valeurs de marché des ETF ont été créées, nous les additionnons pour produire une valeur de marché totale à la fin de chaque barre. Ceci est ensuite transformé en un flux de rendements par la méthode pct_change pour cet objet Series.

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Lele principalLes fichiers CSV intraday sont situés sur le chemin datadir. Assurez-vous de modifier le code ci-dessous pour pointer vers votre répertoire particulier.

Pour déterminer la sensibilité de la stratégie à la période de rétrospective, il est nécessaire de calculer une métrique de performance pour une plage de rétrospectives. J'ai choisi le rendement final total en pourcentage du portefeuille comme mesure de performance et la plage de rétrospective en [50,200] avec des incréments de 10. Vous pouvez voir dans le code suivant que les fonctions précédentes sont enveloppées dans une boucle for à travers cette plage, avec d'autres seuils maintenus fixes. La tâche finale est d'utiliser matplotlib pour créer un graphique linéaire de rétrospectives par rapport aux rendements:

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

Le graphique de la période de lookback par rapport aux rendements peut maintenant être vu. Notez qu'il y a un maximum 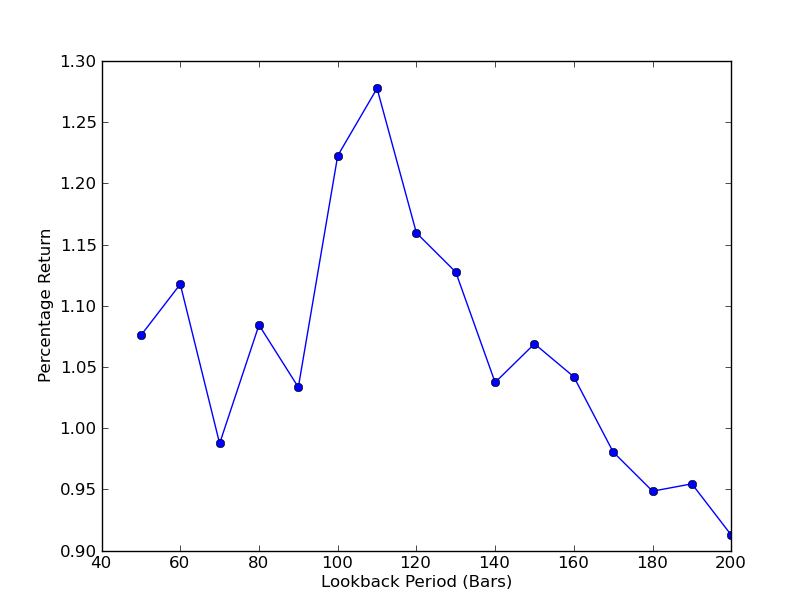global autour d'un lookback égal à 110 barres. Si nous avions vu une situation où le lookback était indépendant des rendements, cela aurait été préoccupant:L'analyse de la sensibilité de la période de rétrospective du ratio de couverture par régression linéaire SPY-IWM

Aucun article de backtesting ne serait complet sans une courbe d'équité en pente ascendante! Ainsi, si vous souhaitez tracer une courbe des rendements cumulés par rapport au temps, vous pouvez utiliser le code suivant. Il tracera le portefeuille final généré à partir de l'étude des paramètres de lookback. Il sera donc nécessaire de choisir le lookback en fonction du graphique que vous souhaitez visualiser. Le graphique trace également les rendements de SPY au cours de la même période pour faciliter la comparaison:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

Le graphique suivant de la courbe des actions est pour une période de référence de 100 jours: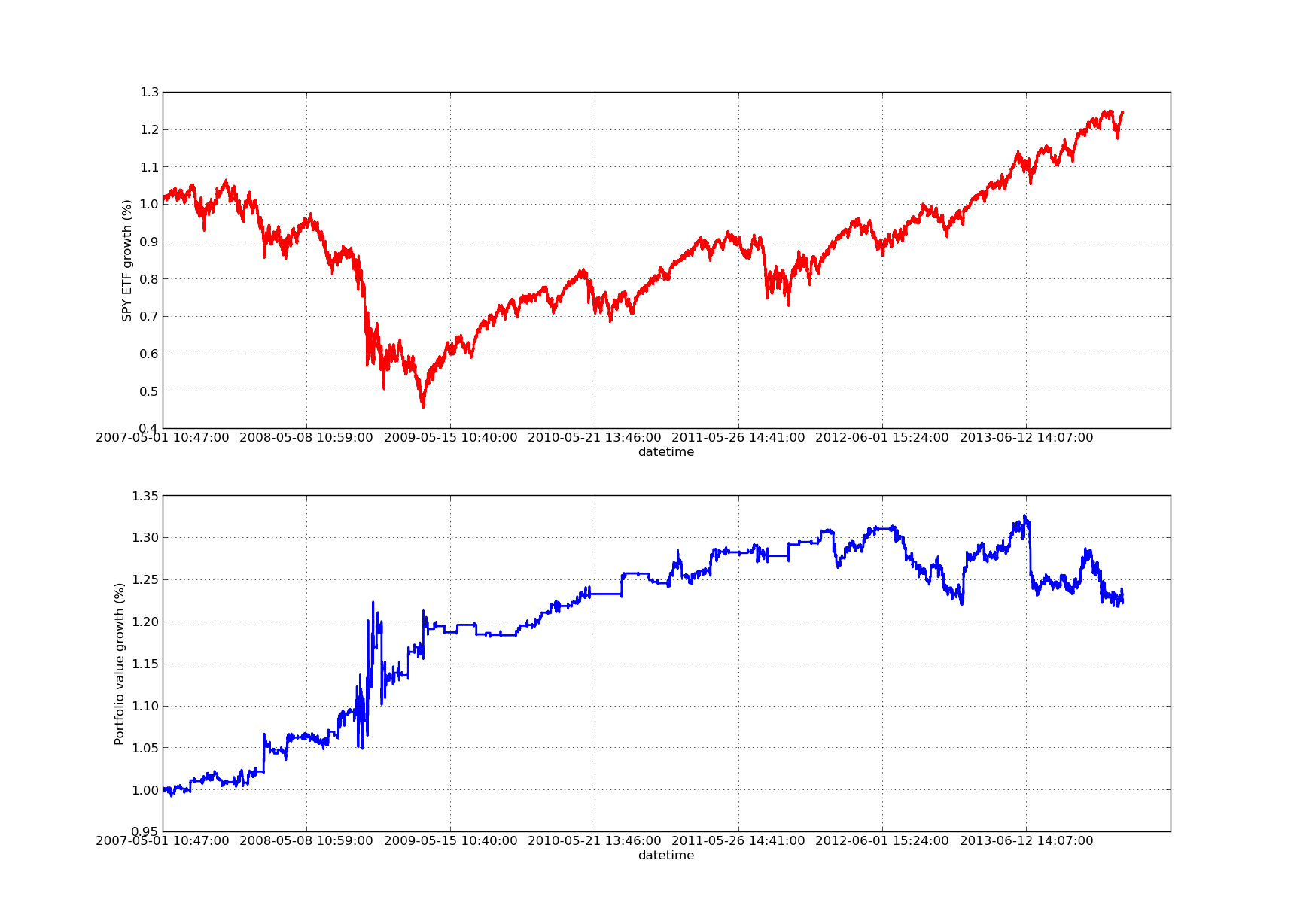L'analyse de la sensibilité de la période de rétrospective du ratio de couverture par régression linéaire SPY-IWM

Il convient de noter que le recours au SPY est important en 2009 pendant la période de crise financière. La stratégie a également connu une période de volatilité à ce stade. Il convient également de noter que les performances se sont quelque peu détériorées au cours de l'année écoulée en raison de la forte tendance du SPY au cours de cette période, ce qui reflète l'indice S&P500.

Notez que nous devons toujours prendre en compte le biais de la tête de recherche lors du calcul du score z de l'écart. En outre, tous ces calculs ont été effectués sans coûts de transaction. Cette stratégie fonctionnerait certainement très mal une fois que ces facteurs sont pris en considération. Les frais, l'écart offre / demande et le glissement ne sont pas pris en compte. En outre, la stratégie consiste à négocier dans des unités fractionnaires d'ETF, ce qui est également très irréaliste.

Dans des articles ultérieurs, nous allons créer un backtester basé sur des événements beaucoup plus sophistiqué qui prendra en considération ces facteurs et nous donnera beaucoup plus de confiance dans notre courbe d'équité et nos indicateurs de performance.