Comment fonctionne le protocole Bitcoin (partie 1)

L’année dernière, j’ai écrit ici 5 idées sur le Bitcoin, et c’est apparemment le premier article sur le Bitcoin que j’ai écrit ici. Aujourd’hui, je vais vous parler du protocole Bitcoin.

Cet article est une traduction de l’article de Michael Nielsen sur le protocole Bitcoin, l’article le plus clair que le traducteur pense avoir écrit sur Bitcoin. Michael Nielsen est un scientifique, écrivain et programmeur pionnier dans la recherche sur le calcul quantique. Pour plus de détails, consultez sa propre présentation. Cette traduction de l’article est due au fait que le traducteur pense que l’article sur Bitcoin et les discussions ont beaucoup, beaucoup de soutien et beaucoup d’opposition.

Juste laisser les gens savoir ce que c’est, où il s’intègre dans l’espace de l’argent électronique, ne pas essayer de les convaincre que c’est bon.

• ### Voici le texte original:

Des milliers d’articles ont tenté d’expliquer Bitcoin, une monnaie en ligne, peer-to-peer. La plupart des articles ont été écrits sur le protocole sous-jacent, en omettant de nombreux détails. Même les articles les plus approfondis ont été bloqués à des points critiques.

Il est difficile de comprendre en profondeur le protocole, car il est facile de prendre Bitcoin pour acquis et de penser à comment l’utiliser pour faire de la spéculation, se demander si c’est une bulle, si cela signifie la fin des impôts, etc. C’est amusant de penser à ces choses, mais elles limitent sérieusement votre compréhension.

J’expliquerai les scripts et les contrats intelligents de Bitcoin dans un prochain article. Pour cet article, je me concentrerai sur les détails du protocole Bitcoin. Pour comprendre cet article, vous devez être familiarisé avec le mot de passe public et la signature numérique associée.

Le Bitcoin est basé sur la cryptographie, et cela peut vous surprendre, mais est-ce que c’est une monnaie ? Est-ce un moyen d’envoyer des messages secrets ? En fait, la plupart des problèmes que Bitcoin veut résoudre sont liés à la protection des transactions, à la garantie que les gens ne peuvent pas voler les choses des autres ou se faire passer pour d’autres personnes, etc. Dans le monde physique composé d’atomes, nous assurons la sécurité par des serrures, des signatures, des coffres-forts bancaires, etc. Dans le monde de l’information, nous assurons la sécurité par la cryptographie.

La stratégie de cet article est de construire Bitcoin en plusieurs niveaux. Nous commencerons par une monnaie numérique très simple, que nous appellerons Infocoin, pour le moment, pour la différencier du Bitcoin. Bien sûr, notre première version d’Infocoin aura beaucoup de défauts, donc nous passerons par plusieurs générations, chaque génération introduisant un ou deux nouveaux concepts. Après plusieurs générations, nous aurons un protocole Bitcoin complet.

C’est un peu plus lent que d’expliquer Bitcoin directement au début. Mais même si vous pouvez comprendre les principes de Bitcoin, il est difficile de comprendre pourquoi Bitcoin a été conçu de cette façon. L’avantage d’une explication plus lente de l’algèbre par étapes est qu’elle vous permet d’avoir une compréhension plus claire de chaque élément de Bitcoin.

Enfin, je dois dire que je suis relativement nouveau dans le monde du Bitcoin. J’ai eu une attention assez superficielle en 2011, mais le début d’une étude sérieuse des détails a eu lieu au début de l’année 2013.

• Première étape: signer une lettre d’intention

  • #### Comment concevoir une monnaie ?

  À première vue, une monnaie numérique semble impossible. Supposons qu’une personne, appelons-la Alice, possède une monnaie numérique qu’elle veut dépenser. Si Alice peut utiliser une chaîne de caractères comme monnaie, comment pouvons-nous l’empêcher d’utiliser la même chaîne de caractères à plusieurs reprises?

  Ce ne sont là que deux des nombreux problèmes à résoudre avec l’information comme monnaie. Dans la première version d’Infocoin, nous avons trouvé un moyen de faire offrir à Alice une chaîne de caractères comme monnaie, et un moyen de la protéger contre la contrefaçon. Supposons qu’Alice donne une infocoin à une autre personne.

  Cette méthode n’est pas particulièrement remarquable, mais elle présente quelques avantages. N’importe qui dans le monde peut utiliser la clé publique d’Alice pour vérifier qu’Alice est bien la personne qui a signé. N’importe qui d’autre ne peut pas produire le résultat de cette signature (cette signature ne peut être générée que par la clé privée possédée par Alice, voir la signature numérique mentionnée ci-dessus), donc Alice ne peut pas dire avec regret non, je n’ai pas donné l’infocoin à Bob.

  Je n’ai pas encore dit ce qu’était l’argent dans ce protocole. Pour être clair: l’argent est le message lui-même. C’est-à-dire que la série de caractères qui a signé le nom représente les caractères que mon amie Alice a donné à Bob pour créer un infocoin.

• Les numéros de série donnent une identité unique à la monnaie

Le problème avec notre première version d’Infocoin est qu’Alice peut envoyer à plusieurs reprises le même message signé à Bob. Supposons que Bob reçoive 10 messages de ce type. Je me demande, Alice, si elle a donné un infocoin à Bob.

Nous voulons que l’infocoin ait une identité unique. Il faut une étiquette ou un numéro de série. Alice peut signer un infocoin avec le numéro de série 8740348 dans un message.

Pour que ce système fonctionne, nous devons avoir une source fiable de numéros de série. Une façon de générer des numéros de série est de créer une institution comme une banque. Cette banque va générer des numéros de série pour les infocoins, enregistrer qui possède quelles infocoins, et vérifier l’authenticité des transactions.

Plus précisément, supposons qu’Alice va à une banque et lui dit: “Je veux prendre un infocoin de mon compte”. La banque retire un infocoin de son compte, puis lui donne un nouveau numéro de série jamais utilisé, supposons que ce soit 1234567. Puis, quand Alice veut envoyer un infocoin à Bob, elle signe ce nouveau message: “Alice veut donner à Bob un infocoin de la série 1234567”. Mais Bob n’accepte pas seulement l’infocoin, mais il contacte la banque et confirme deux choses: premièrement, l’infocoin de la série 1234567 appartient à Alice.

• ### Que tout le monde soit une banque.

La solution ci-dessus semble avoir beaucoup de potentiel. Cependant, nous pourrions faire quelque chose de plus ambitieux. Nous pourrions supprimer les banques du protocole. Cela change radicalement les propriétés de la monnaie elle-même.

La méthode consiste à faire en sorte que tout le monde collabore pour devenir une banque. En particulier, supposons que chaque personne qui utilise infocoin conserve un registre complet, qui comprend quel infocoin appartient à qui. Vous pouvez imaginer cela comme un livre ouvert partagé qui enregistre toutes les transactions d’infocoin.

Maintenant, supposons qu’Alice donne une infocoin à Bob. Elle signe une infocoin à Bob avec le numéro de série 1234567 dans la boîte de messagerie. Et Bob peut vérifier avec sa propre chaîne de blocs, OK, c’est bien l’infocoin qu’Alice m’a donné.

Nous avons toujours le problème de savoir d’où vient le numéro de séquence de l’infocoin, mais c’est un problème facile à résoudre, alors j’explique plus tard. Le problème plus difficile est que le protocole permet à Alice de dépenser à plusieurs reprises son infocoin. Elle peut publier un message signé disant: Alice va donner à Bob un numéro de séquence d’infocoin de 1234567, et elle peut aussi publier un message signé disant: Alice va donner à Charlie un numéro de séquence d’infocoin de 1234567. Bob et Charlie utilisent tous deux leur propre blockchain pour vérifier que l’infocoin vient bien d’Alice.

Nous appelons ce problème le double-spending, et à première vue, il semble très difficile de réussir. Après tout, si Alice envoie un message à Bob, puis Bob envoie un message à tous les autres (y compris Charlie), les autres ont mis à jour leur blockchain. En ce moment, Charlie ne sera pas trompé par Alice.

La solution la plus simple est que lorsque Alice envoie un infocoin à Bob, Bob ne devrait pas vérifier la transaction seul. Il devrait plutôt publier cette transaction attendue sur l’ensemble du réseau infocoin, afin que d’autres personnes puissent aider à juger si la transaction est légitime.

Pour être plus précis, supposons qu’Alice veut donner un infocoin à Bob. Comme avant, elle donne une signature à un message, elle donne à Bob un code infocoin avec le numéro de série 1234567 et signe le message de bonne réputation à Bob. Comme avant, Bob fait une vérification avec sa propre blockchain, la pièce appartient à Alice. Mais le protocole est différent, Bob ne l’accepte pas directement, mais publie le message d’Alice sur l’ensemble du réseau.

Il y a beaucoup d’incertitudes concernant ce protocole. Par exemple, qu’est-ce que cela signifie que si suffisamment de personnes publient le message, combien de personnes sont suffisantes? Il ne peut pas s’agir de l’ensemble du réseau infocoin, car nous ne savons pas à l’avance qui est sur le réseau infocoin. De même, il ne peut pas s’agir d’une partie fixe des utilisateurs.

• ### Une preuve de travail

Supposons qu’Alice veuille dupliquer le réseau infocoin dans les accords mentionnés ci-dessus. Supposons qu’elle utilise un système automatisé pour créer de nombreux comptes avec différentes identités sur le réseau infocoin, en supposant qu’il y en ait un milliard. Comme précédemment, elle tente de dupliquer, en donnant le même infocoin à Bob et Charlie, mais lorsque Bob et Charlie demandent au réseau infocoin de vérifier la transaction, l’acétate d’Alice inonde tout le réseau, en disant à Bob et Charlie qu’ils peuvent passer par cette transaction et peut-être tromper l’un d’entre eux ou les deux pour accepter la transaction.

Il existe une méthode intelligente appelée “Proof-of-work” qui utilise une méthode appelée “Proof-of-work”. Cette méthode n’est pas intuitive et nécessite une combinaison de deux concepts: 1) faire vérifier artificiellement une transaction coûte un coût de calcul élevé; 2) récompenser ceux qui aident à vérifier cette transaction.

C’est l’essentiel du certificat de travail. Mais pour vraiment comprendre le certificat de travail, nous devons aller plus loin dans les détails.

Supposons qu’Alice donne un message à l’ensemble du réseau. Supposons qu’Alice donne à Bob un infocoin avec le numéro de série 1234567. Lorsque les autres membres du réseau l’entendent, chacun l’ajoute à une liste de transactions en attente qui n’ont pas encore été approuvées par le réseau.

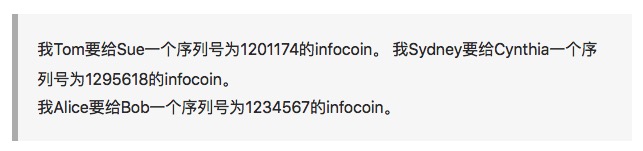
David examine sa propre blockchain et voit que les transactions mentionnées ci-dessus sont justifiées. Il veut aider à diffuser le message de validation à l’ensemble du réseau. Cependant, avant cela, le protocole de vérification des transactions exige de David qu’il résolve un casse-tête de calcul, la preuve de travail.

Pour l’expliquer, nous utilisons une fonction de hachage fixe que tout le monde sur le réseau connaît. Nous l’incluons dans le protocole lui-même. Bitcoin utilise une fonction de hachage SHA-256 bien connue, mais n’importe quelle fonction de hachage cryptographique peut être utilisée ici. Nous donnons à David un marqueur de transaction en attente, le code L, pour qu’il puisse le référencer ultérieurement.

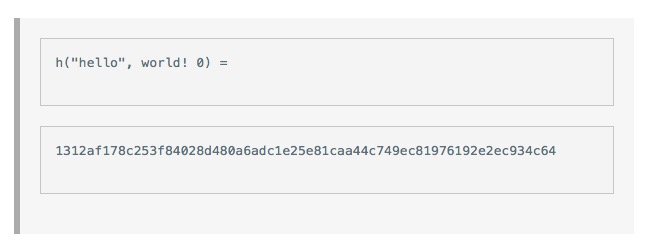
Le problème que David va résoudre est de trouver un nombre aléatoire x qui, lorsque nous ajoutons ce x derrière L et que nous hachons cette combinaison, commence par plusieurs zéros. La difficulté de ce problème peut être réglée en ajustant le nombre de zéros de départ.

Vous pouvez voir que cela ne fonctionne pas quand x est égal à 1.

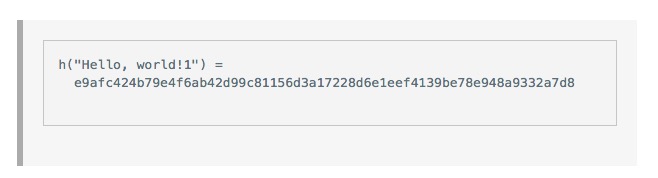
Et puis nous avons essayé x est égal à 2, et puis x est égal à 3, 4, 5… et nous savons que finalement, quand nous avons trouvé x est égal à 4350, nous avons obtenu

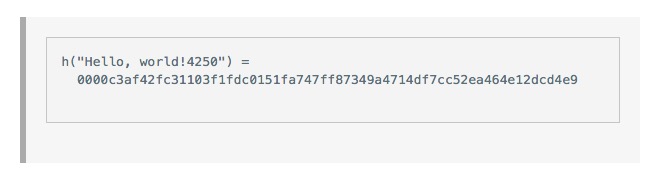
Ce nombre aléatoire x nous donne un résultat de quatre hachages commençant par zéro. Cela suffit pour résoudre un simple problème de démonstration du travail de l’axe sur l’axe.

Ce qui rend ce casse-tête difficile à résoudre, c’est que les résultats de la fonction de hachage de code sont toujours aléatoires, et que toute modification mineure de la valeur d’entrée va complètement différer les résultats de sortie de la fonction de hachage entière, de sorte qu’il est difficile de les prédire. Donc, si nous avons besoin de résultats de sortie qui doivent commencer par 10 zéros, David aura besoin d’une moyenne de 1610 ≈ 1012 x différents pour trouver la valeur appropriée.

Il est évident que l’on peut contrôler la difficulté des problèmes de preuve de travail en spécifiant combien de zéros sont nécessaires. En fait, le protocole Bitcoin a un meilleur contrôle sur la difficulté des problèmes en modifiant légèrement la preuve de travail ci-dessus.

Eh bien, supposons que David ait eu la chance de trouver une bonne x (nonce), félicitations ! (il sera récompensé pour avoir trouvé cette réponse). Il publiera qu’il a prouvé que les transactions dans ce bloc sont légitimes, et en même temps publiera la valeur de x qu’elle a trouvée, et les autres participants de l’infocoin pourront prouver que la solution de x qui fonctionne est valide. Ensuite, ils mettront à jour leur propre blockchain pour inclure les transactions publiées par David.

Pour que le travail de preuve fonctionne, les participants du réseau devraient avoir un incitatif pour aider à vérifier les transactions. Sans incitatif, personne ne serait prêt à dépenser son propre pouvoir de calcul pour aider à vérifier les transactions. Si les participants du réseau ne sont pas disposés à dépenser leur pouvoir de calcul, le système ne fonctionnera pas.

Dans le protocole de Bitcoin, ce processus de validation est appelé “mining”. Chaque validateur de chaque bloc de transaction reçoit un bitcoin en récompense. Au début, il était de 50 bitcoins. Cependant, pour chaque bloc de 210.000 validateurs (c’est-à-dire environ tous les 4 ans), la récompense est réduite de moitié. Cela n’est arrivé qu’une seule fois jusqu’à présent, c’est-à-dire que la récompense pour la validation d’un bloc est de 25 bitcoins.

Vous pouvez considérer la preuve de travail comme un processus de validation de transactions concurrentielles. Chaque participant dépense une partie de la puissance de calcul de l’ordinateur. Les chances d’un mineur de gagner sont approximativement égales à la taille de la puissance de calcul qu’il contrôle par rapport à la puissance de calcul de l’ensemble du réseau. Par exemple, si un mineur contrôle un pour cent de la puissance de calcul de l’ensemble du réseau, sa probabilité de gagner est approximativement de un pour cent.

Bien sûr, même si les mineurs malhonnêtes n’ont qu’une petite chance de détruire la blockchain, nous n’avons pas la confiance nécessaire pour l’utiliser comme monnaie.

J’analyse immédiatement le problème des deux fleurs, mais avant cela, j’aimerais ajouter un détail important dans le concept d’Infocoin. Idéalement, nous souhaitons que le réseau d’Infocoin puisse unifier l’ordre dans lequel les transactions se produisent. Si nous n’avons pas d’ordre unifié, il n’est pas très clair qui a quelle infocoin à un moment donné.

Par hasard, il arrive que des branches soient créées sur une même blockchain. Cela est dû au fait que, parfois, deux mineurs valident presque simultanément la transaction d’un même bloc. Ils sont publiés simultanément sur le réseau, certains mettant à jour leur blockchain d’une manière et d’autres d’une autre.

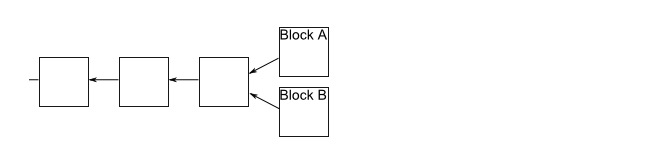
Cela crée une situation que nous voulons éviter, où l’ordre des transactions n’est pas clair et où l’on ne sait pas qui possède quelle infocoin. Heureusement, il existe un moyen simple de déplacer les branches. La règle est la suivante: si les branches se produisent, les gens sur le réseau continuent à maintenir deux branches et, en tout cas, les mineurs ne travaillent que sur la plus longue des chaînes de blocs.

Supposons que nous ayons une branche, et que certains mineurs aient reçu le bloc A en premier, tandis que d’autres aient reçu le bloc B en premier. Les mineurs du bloc A continueront à miner le long de leur branche, tandis que d’autres continueront à miner le long de la branche du bloc B. Supposons que les mineurs du bloc B soient les premiers à réussir à miner le bloc suivant:

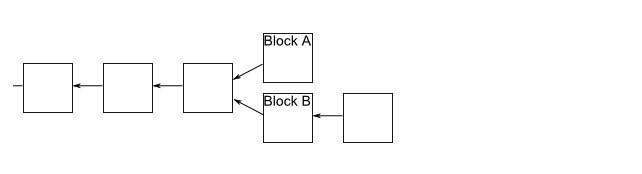
Quand ils reçoivent ce message, les gens de la branche A remarquent que la branche B est maintenant la plus longue et passent à la branche de B. Le travail sur la branche A s’arrête rapidement, de sorte que tout le monde travaille sur la même chaîne de blocs. Le bloc A est alors ignoré.

De la même manière, si un mineur de la branche A atteint le bloc suivant, alors un mineur de la branche B s’arrête et passe à la branche A.

Quel que soit le résultat, ce processus garantit que la chaîne de blocs a une séquence unifiée. Dans Bitcoin, une transaction ne peut pas être considérée comme confirmée tant que 1) elle n’existe pas dans le bloc de la branche la plus longue, et 2) au moins 5 blocs validés ont été validés après elle. Dans ce cas, nous disons que la transaction a 6 tranches de confirmation. Cela donne à l’ensemble du réseau le temps d’unifier l’ordre des blocs.

Maintenant que nous comprenons la chronologie, revenons sur ce qui se passerait si une personne malhonnête voulait dépenser deux fois plus. Supposons qu’Alice veuille donner la même transaction à Bob et à Charlie en même temps. Une possibilité est de lui demander de vérifier un bloc avec deux transactions en même temps.

Mais une autre possibilité est qu’elle essaie de publier deux transactions séparément. Elle pourrait publier une transaction pour une partie des mineurs et une autre pour une autre partie des mineurs, et elle souhaite que les deux transactions soient vérifiées. Heureusement, dans ce cas, comme nous venons de le dire, le réseau ne confirme finalement qu’une seule des transactions. Donc, ce n’est pas un problème non plus.

Une autre possibilité est que Alice = Bob, c’est-à-dire qu’Alice essaie de donner une pièce à Charlie et qu’elle la donne à elle-même, car elle peut avoir plusieurs comptes. Dans ce cas, la stratégie d’Alice est d’attendre que Charlie accepte l’Infocoin, c’est-à-dire après que la transaction ait été confirmée environ 6 fois dans la plus longue chaîne de blocs.

Malheureusement, à ce moment-là, Alice était déjà six étapes en retard par rapport à la plus longue chaîne de blocs. Elle avait du mal à suivre la plus longue branche. Les autres mineurs ne l’aideraient pas, car ils devaient tous travailler sur la plus longue branche pour être récompensés.

Bien sûr, ce n’est pas très strict pour dire qu’Alice ne peut certainement pas faire double jeu. C’est juste une conclusion raisonnable. Le livre blanc de Bitcoin n’a pas fait une analyse de sécurité rigoureuse, mais une conclusion informelle similaire à la mienne.

Michael, l’auteur de la première moitié, a laissé de côté le concept d’Infocoin et a donné un aperçu plus détaillé du protocole Bitcoin en utilisant la vue de la transaction Bitcoin. Si vous avez vu cela ici, vous pouvez suivre mon blog sur Weibo et mon blog.

Si vous trouvez cela utile, nous vous recommandons de donner un conseil à l’auteur de cet article, Michael Nielsen, 17ukkKt1bNLAqdJ1QQv8v9Askr6vy3MzTZ, que vous pouvez également suivre sur Twitter, ou de vous intéresser au premier chapitre de son nouveau livre sur les réseaux neuronaux et l’apprentissage profond qui sera publié prochainement.

Il a été créé par les parents d’un jeune garçon, Jean-Pierre, qui a grandi dans une famille pauvre.