PS: L’article est assez long, il ne s’agit pas d’un gros article, je vous conseille de le lire, ça vous aidera sûrement.

La méthode de négociation en grille est essentiellement une méthode de négociation basse et basse, basse et haute, basse et haute, basse et haute, basse et haute, basse et haute, basse et haute, basse et haute, basse et basse, basse et haute. La méthode de négociation en grille ne repose pas sur la pensée artificielle, mais est un acte purement procédural.

La méthode de négociation sur grille peut être programmée, ne nécessite pas de stockage à long terme, est sûre et sans souci de stabilité des gains. C’est pourquoi la méthode de négociation sur grille est la méthode de profit stable la plus adaptée à la participation des gens ordinaires, car cette méthode exige peu d’expérience professionnelle et est très universelle.

Règles de transaction détaillées de la loi de transaction de grille

Une simple comparaison: commencez par diviser votre argent en deux parties égales: une partie est achetée immédiatement pour les actions ou les fonds que vous aimez, et l’autre partie est mise en réserve dans votre poche. Si les actions ou les fonds que vous achetez continuent à tomber, vous prenez l’argent de votre poche et vous le mettez en réserve. La plupart des logiciels de négociation sont intégrés, les utilisateurs peuvent automatiser le fonctionnement en les configurant simplement. La série de articles de la colonne de l’univers de la méthode de négociation de grille contient des tutoriels de configuration, les amis intéressés peuvent consulter le contenu de la colonne et apprendre directement les tutoriels de configuration du logiciel.

Il existe de nombreuses variantes de la méthode de grille, et voici l’une des plus célèbres, qui explique pourquoi votre compte gagne de plus en plus d’argent, et qui explique les principes scientifiques de la méthode de grille pour gagner de l’argent de manière stable.

Chaque boursier a vécu cette expérience: une action a grimpé à la hausse, puis est revenue à la baisse, a eu du mal, a regretté secrètement, a vendu plus tôt. En fait, sans regret, l’un des plus grands scientifiques du monde, l’inventeur de l’informatique Shannon, nous a aidé à trouver une solution.

Dans la seconde moitié de sa vie, Shannon a principalement étudié les investissements, donnant régulièrement des conférences pour enseigner les techniques secrètes. Une année, Shannon a donné une conférence dans la plus grande salle de conférence du MIT, où il a enseigné les secrets de la façon de gagner de l’argent dans ces conditions.

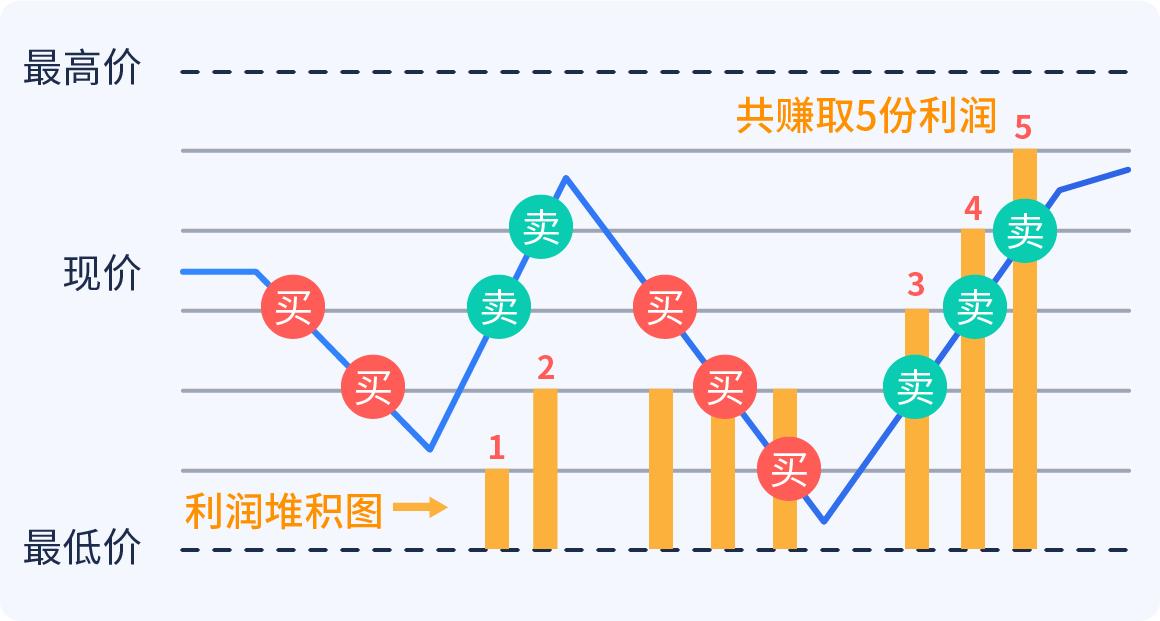
Les adeptes de cette énigme l’appellent le démon de Shannon, et le démon de Shannon est une sorte de mécanisme de transaction de grille dont on parle beaucoup.

La recette de Shannon est la suivante:

Imaginons qu’une action monte de 1 à 2 et qu’elle baisse de 2 à 1, que feriez-vous ?

Si vous êtes prêt à investir 200 dollars, le secret de Shannon est que vous achetez 100 dollars d’actions, 100 dollars d’actions vides, et tout ce que vous avez à faire est de maintenir la valeur marchande de l’action et le montant total de la trésorerie.

Par exemple, si vous attendez jusqu’à ce que 100 actions augmentent à 200, vous avez 200 actions plus 100 de l’argent, le total des actifs est de 300, alors vous vendez 50 dollars d’actions, donc vous avez 150 actions, 150 dollars d’argent, et lorsque les actions baissent de 1 pièce, la valeur marchande de l’action est de seulement 75, mais votre total des actifs est de 225!

Si les actions commencent à baisser puis à remonter, et qu’il en résulte la même chose, vous aurez gagné 25 dollars !

Cela peut sembler impossible, mais les actions ont doublé, et la baisse de la moitié de la baisse est égale à: 2 × 0.5-1 = 0, c’est un pas en avant, et la stratégie de Shannon de ramener les prix à leur point de départ a réellement fait de l’argent.

Le secret de la fortune de Shannon réside dans l’utilisation de la formule de Kelly, la fourchette la plus puissante de l’univers.

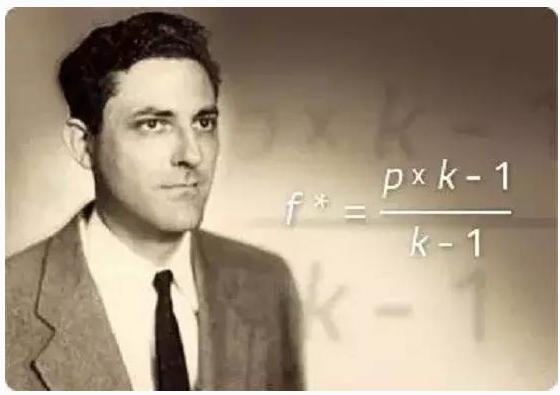
Cette formule a été utilisée par Kelly, un collègue de Shannon chez Bell Labs, pour investir dans des applications de traitement des signaux de communication basées sur l’informatique de Shannon.

La formule de Kelly est connue dans le monde de l’investissement sous le nom de formule de la fortune de Kelly, qui traite de la question de savoir comment calculer le meilleur ratio d’investissement dans un pari ou un investissement en fonction de la probabilité des pertes.

La formule générale de l’équation de Kelly est la suivante: f = (pb-q) / b

Par exemple, P est la probabilité que vous gagniez de l’argent (positif par exemple), q est la probabilité que vous perdiez de l’argent, et dans le jeu de lancer des pièces, ces deux valeurs sont exactement égales à 0.5, b est quoi? b est votre chance de gagner, c’est combien d’argent vous pouvez gagner en perdant votre argent.

Par exemple, pour chaque fois que vous misez 1 pièce, et que le joueur vous donne 6 pièces, alors b est égal à 5 — 6 pièces moins 1 pièce de votre argent principal, dans ce cas, l’argent que vous devriez miser pour chaque fois est f = — 5 × 0.5-0.5) / 5 = 40%, dans ce pari, vous misez 40% de votre argent pour chaque fois, et votre rendement géométrique est le plus élevé possible!

Il n’y a pas d’arrangement de ratio d’investissement meilleur que la formule de Kelly !

Le principe de l’équation de Kelly est en fait très simple, pour la valeur future totale de votre actif: C = {\displaystyle C={1}+fb}^Np*(1-fa) ^ Nq (f: pourcentage d’investissement, b la probabilité de gagner, a la probabilité de perdre, Np le nombre de victoires, Nq le nombre de défaites), pour une derivation de C avec f comme variable, on obtient le meilleur f, cette formule est: f = p/a-q/b

Cette formule ne ressemble pas à la formule précédente f = {pb-q) / b, mais elle est la même, si vous perdez, vous perdez tout (par exemple, si vous lancez une pièce de monnaie sur la face opposée, vous perdez le dollar que vous avez misé) alors a est égal à 0, et a est égal à 0, c’est la même chose que la formule précédente.

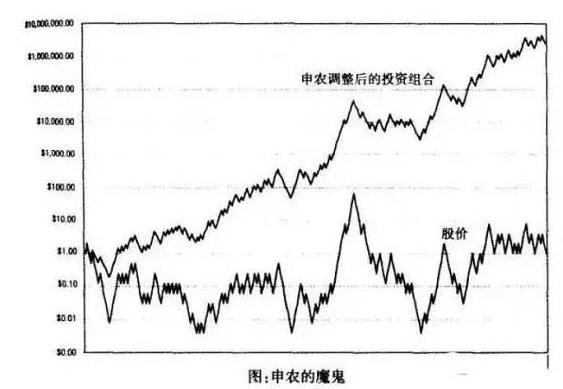
Si vous utilisez la formule de Kelly pour examiner le Diable de Shannon, le doublement en hausse correspond à un pari de 1 pièce, le gagnant vous donne 2 pièces, et la réduction en baisse correspond à un pari de 1 pièce, la perte, le joueur reçoit 5 pièces. Sur la base de ces informations, l’utilisation de la formule de Kelly ci-dessus permet de calculer la position optimale du Diable de Shannon: f = p/a-q/b = 0.⁵⁄₀.5-0.⁵⁄₁ = 0.5

C’est le secret du diable de Shannon, le meilleur taux d’investissement calculé par la formule de Kelly est d’investir la moitié de l’argent, c’est pourquoi chaque fois que Shannon a besoin d’être ajusté à la valeur marchande, le principe derrière cela est le même.

Si Shannon continue à jouer avec cette stratégie, combien de dollars gagnera-t-il ?

Le processus déduit de l’équation de Kelly présentée ci-dessus est connu sous le nom de C = {\displaystyle C={1}+0.5×1}^Np*(1-0.5 × 0.5) ^ Nq, en supposant que la probabilité d’augmentation ou de diminution est égale sur le long terme, Np = Nq = n, le résultat est:

En d’autres termes, si les actifs de Shannon augmentent de 1,125 fois n, cela ne semble-t-il pas être un profit excessif et effrayant ?

Mais cela va à l’encontre de l’intuition, n’est ce pas ?

Il est monté, il est tombé, il est tombé, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté, il est monté,

Si nous étudions de plus près, nous découvrons une faille, investir un dollar en hausse, mais investir un dollar en baisse ne fait que perdre 0,5, selon le calcul de la probabilité d’attente: 1 × 0,5-0,5 × 0,5 = 0,25, cette impasse est évidemment un rendement attendu positif.

Mais si c’est un jeu où il y a un gain positif, pourquoi garder tout ce que vous avez et ne rien gagner à la fin ?

C’est un phénomène très intéressant, et il y a une relation très importante entre votre rendement final et votre taux de détention !

La mauvaise position peut vous faire perdre un centime dans un jeu où les gains sont positifs.

Si nous utilisons le concept de profit pour mesurer le diable de Shannon et que nous trouvions que ce profit est: 2 × 0.5 = 1 (2: doubler, 0.5: contrepartie), alors il n’y aura jamais de profit dans ce jeu, il n’y aura jamais de profit.

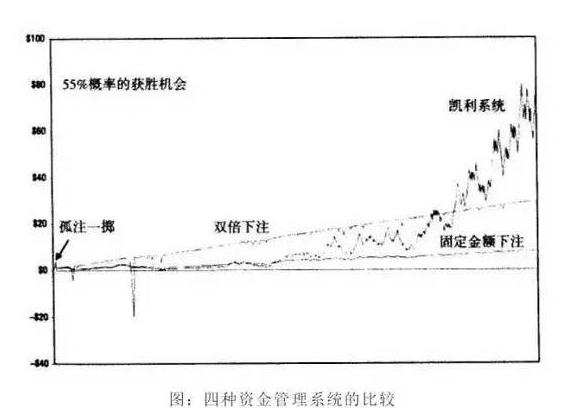
La formule de Kelly est une formule magique qui permet de réduire à zéro le taux de rendement géométrique et de créer une richesse infinie.

Si nous pensons plus profondément au diable de Shannon, nous pourrions penser que les hausses et les baisses sont réduites à zéro et que nous pouvons gagner de l’argent, ce n’est pas scientifique, le problème est certainement de gagner 1 dollar et de perdre seulement 0,5 $.

En réalité, c’est peut-être l’inadéquation de ces deux probabilités qui cause l’illusion que la probabilité de doubler est probablement inférieure à la probabilité de baisser de moitié, de sorte que si la probabilité de l’équation ci-dessus est modifiée, vous ne pouvez pas gagner de l’argent.

Et le diable de Shannon suggère que les probabilités sont égales. Est-ce que ce n’est pas une idée raisonnable de penser que les deux probabilités ne sont certainement pas les mêmes, ou bien est-ce que ce n’est pas stupide de faire de l’argent à partir de rien ?

Donc nous allons voir si la probabilité d’une hausse d’un double est la même que la probabilité d’une baisse d’un demi.

L’un a augmenté de 100%, l’autre a diminué de 50%, mais cela n’a pas l’air du tout de la même chose, il est évident que le chiffre d’une augmentation de 100% est plus petit que celui d’une baisse de 50%.

Et lentement, 100% et 50% ne sont qu’une amplitude, pas une probabilité, en ce qui concerne les rendements boursiers, l’académique et la pratique utilisent le rendement logarithmique, bien que la pratique montre que le rendement logarithmique ne correspond pas parfaitement à la distribution normale, mais après tout, l’approximation est très élevée.

Avant d’avoir un meilleur modèle, nous pourrions commencer par examiner le rendement de la paire par une distribution normale et répondre directement: La probabilité d’une hausse de 100% et d’une baisse de 50% est la même dans une distribution normale de rendement logarithmique !

Dans une situation de parité de probabilité, avec un rendement à long terme de 0, vous pouvez gagner de l’argent avec le diable de Shannon, ce n’est pas très fort !

Alors, combien peut-on gagner avec 50 places sur 50 places ?

Pour calculer le rendement logarithmique de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équivalent de l’équ Donc, la probabilité de baisse de 10% que nous appelons habituellement est: -9.09%, avec une probabilité de 0,5, et nous avons une probabilité de -10%, avec une probabilité de baisse de 9,09%.

En utilisant la formule de Kelly pour calculer le ratio de détention optimal, nous n’aurons plus qu’à vendre et acheter avec les diaboliques actions de Shannon, maintenir un ratio de détention fixe, et nous pourrons réaliser les diaboliques gains de Shannon !

Selon la formule de Kelly précédente: f=p/a-q/b, on introduit la probabilité et la cote que nous venons de calculer: f=0.⁵⁄₀.0909-0.⁵⁄₀.1=5.5005-5=0.5005, ce qui est presque égal à 0.5。

Le ratio de détention optimal calculé selon la formule de Kelly est donc de 50% des positions (si vous changez 10% en 30%, le taux de détention est de 200%, le double du levier).

Je l’ai déjà dit plus haut dans ma déduction de la formule de Kelly:

C=（1+fb)^NpDonc, nous avons ajouté le nombre que nous venons de calculer à 1 fa^Nq. C=(1+0.5×0.1)(1-0.5×0.0909)^n=(1.05×0.95455)^n=1.0022^n

Conçue selon la formule de Kelly pour un ratio d’investissement parfait, la machine qui effectue des transactions parfaites dans un espace de 19.09% d’amplitude peut générer un bénéfice net de 0.22% sur chaque transaction dans le marché, sans tenir compte des coûts de transaction, dans le cas d’une distribution normale du taux de rendement symétrique du marché boursier.

Dans le cadre de la règle, ce taux de marge est le taux de croissance le plus rapide par rapport au capital du compte, ce qui est le principe de base selon lequel la gestion des positions peut être utilisée pour stabiliser les bénéfices dans le cas où 0 est l’attente.

En résumé, la méthode de négociation de grille est une bonne méthode de négociation, mais il y a aussi des inconvénients, c’est-à-dire que les règles peuvent ne pas fonctionner, comme la peur de la rupture de la grille, la peur d’une seule partie, etc. Si vous voulez utiliser la méthode de négociation de grille en toute sécurité, vous devez résoudre ces inconvénients.

Pour partager quelques idées sur les méthodes de négociation de grilles: Les règles de trading de la loi de la grille de commerce détaillées Les principes scientifiques de la stabilité des profits Les avantages et les inconvénients de la méthode de la grille et comment optimiser la stratégie L’optimisation des stratégies de la loi de la grille - comment choisir le bon type d’investissement L’optimisation des stratégies de la loi de la grille - résoudre le problème de la chute unilatérale et réduire le taux de rupture L’optimisation de la stratégie de la grille de négociation - comment utiliser la gestion de position pour un déblocage rapide Le système de grille a été optimisé et les bénéfices de la grille ont été multipliés par cinq. Une stratégie de grille pour modifier la stratégie de balayage à haute fréquence