s a incités à décider de diviser l’échantillon en deux périodes d’un an.

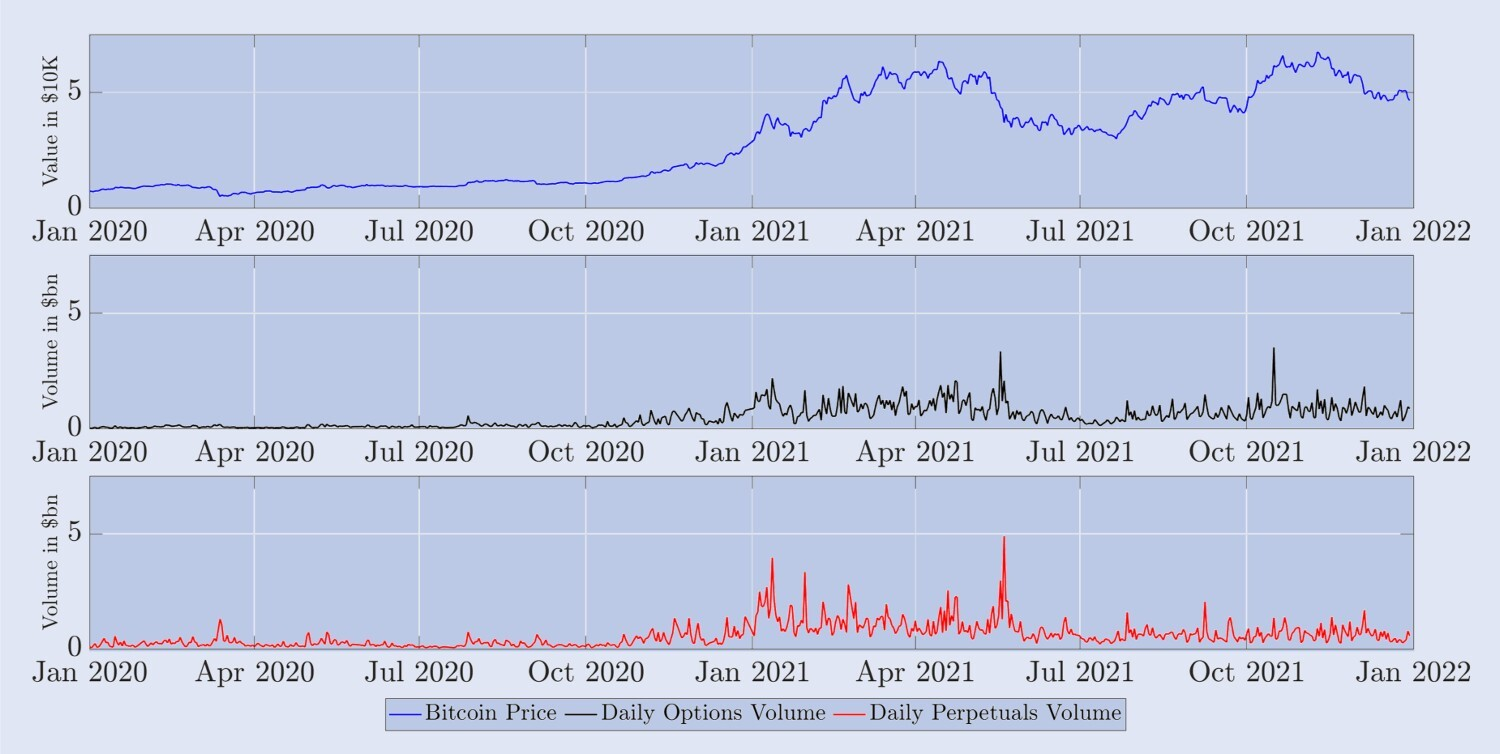
Figure 5. Évolution de l’indice BTC et du volume quotidien des échanges de produits dérivés.

Le graphique ci-dessus montre le prix de l’indice BTC à 00h00 UTC quotidiennement pour une période d’échantillonnage de deux ans commençant le 1er janvier 2020 (en haut, graphique bleu) ; le volume total correspondant sur 24 heures de toutes les options sur Deribit (au centre, noir) graphique) ; et le volume quotidien des échanges de contrats perpétuels (en bas, graphique rouge). La valeur de l’indice BTC est en unités de 10 000 $ et le volume des transactions est en milliards de dollars.

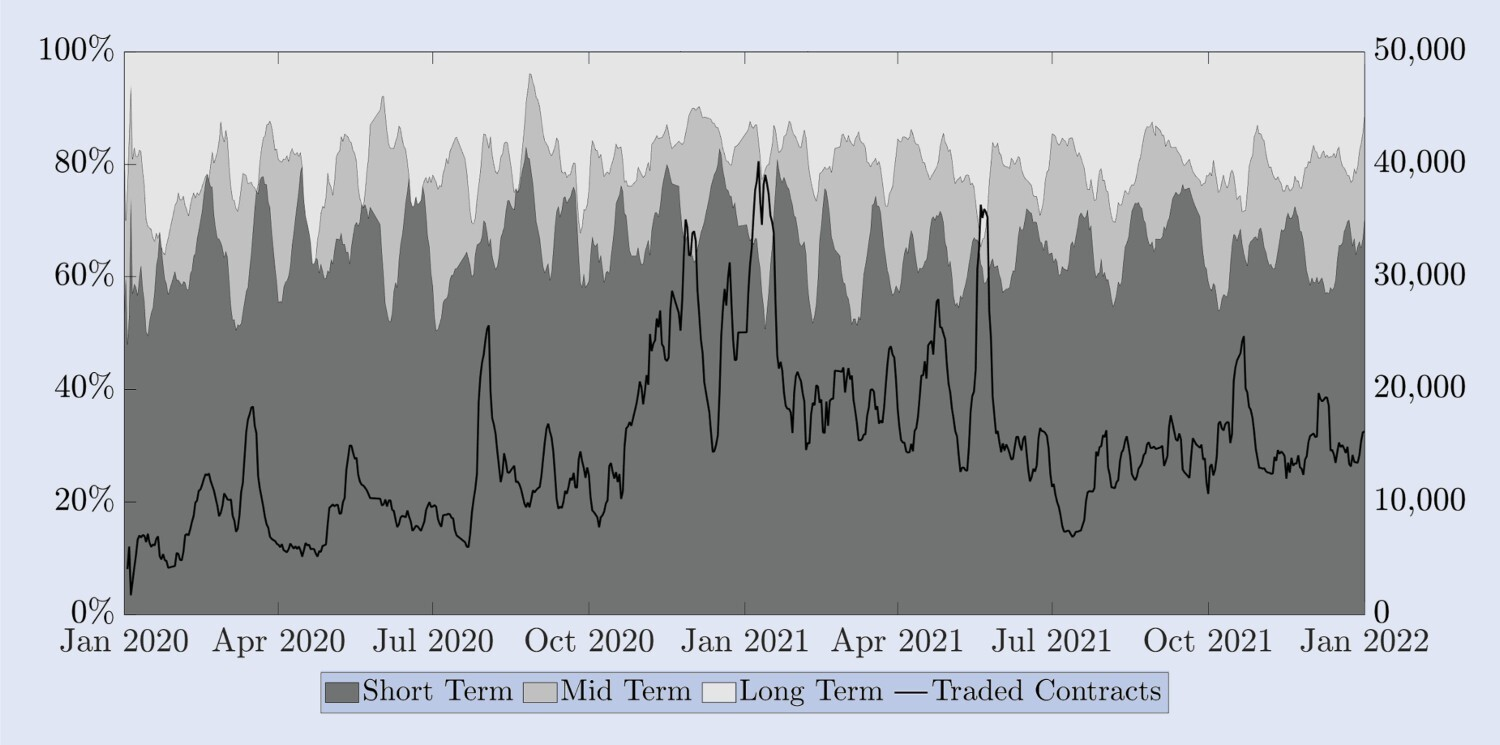
Alexander et al. (2022b) documentent de nombreuses différences entre les marchés d’options Bitcoin et S&P 500. L’une des principales différences réside dans la proportion d’options courtes, moyennes et longues négociées. Les options d’un mois sur le S&P 500 sont relativement à court terme, car la plupart des transactions ont lieu entre un et trois mois d’expiration. Cependant, une option Bitcoin avec une date d’expiration d’un mois entre dans la catégorie à plus long terme. Pour mettre cela en perspective, la figure 6 illustre la proportion de contrats négociés par heure d’expiration sur Deribit. La ligne continue sur l’échelle de droite représente le nombre de transactions pour tous les contrats expirant. Pour plus de clarté, nous présentons ces données en utilisant des moyennes hebdomadaires sur une fenêtre glissante. La tendance saisonnière de la proportion d’options à court terme (jusqu’à deux semaines) est le résultat de la politique de programmation des émissions, selon laquelle, à moins qu’une option mensuelle ou trimestrielle standard n’expire au cours de cette semaine (ou de ces deux semaines), une option Des options à échéance d’une semaine (et/ou de deux semaines) seront émises pour la semaine en cours (ou les deux semaines). Sur l’échelle de gauche, nous présentons la part des maturités à court terme (jusqu’à deux semaines), à moyen terme (entre deux semaines et un mois) et à long terme (plus d’un mois). Pour ce faire, nous regroupons tous les contrats négociés au cours de la journée dans chaque catégorie d’expiration et les présentons sous forme de pourcentage de tous les contrats négociés, en utilisant à nouveau une moyenne hebdomadaire sur une fenêtre mobile pour plus de clarté. Outre ce schéma saisonnier, sur l’ensemble de la période de deux ans, seulement 15 à 20 % des transactions ont été effectuées sur des options avec des dates d’expiration supérieures à un mois. Malgré l’augmentation du nombre de contrats négociés dans notre échantillon, la proportion de contrats avec des dates d’expiration de plus d’un mois est restée relativement stable, tout comme la proportion d’options à court terme expirant dans les deux semaines. En fait, environ 60 % de tous les contrats négociés se situent dans ces périodes d’expiration à très court terme. 20 à 25 % supplémentaires des contrats négociés correspondent à des options « à moyen terme » avec des périodes d’expiration comprises entre deux semaines et un mois. Étant donné que les options avec une période d’expiration d’un mois représentent 80 à 85 % de l’ensemble du volume des transactions sur Deribit, nous avons décidé de concentrer nos recherches de couverture sur ces options. Les options avec des échéances supérieures à un mois présentent trop de prix obsolètes pour être utiles dans notre analyse empirique, même à des fréquences horaires. Cela nous incite à considérer une option dans chacune des catégories d’expiration documentées ci-dessus. Pour faciliter la comparaison, nous avons sélectionné des options d’expiration constante de 10, 20 et 30 jours comme objets de recherche, chacune d’entre elles étant un proxy pour les trois principales catégories d’expiration.

Fig. 6. Date d’expiration des options négociées.

L’échelle de gauche montre la proportion d’options à court terme (jusqu’à deux semaines, gris foncé), d’options à moyen terme (entre deux semaines et un mois, gris moyen) et d’options à long terme (plus d’un mois, (gris clair) dans le volume total des échanges. La ligne noire (échelle de droite) représente le nombre total de contrats d’options négociés. Toutes les séries sont des moyennes hebdomadaires mobiles de données quotidiennes.

Nous discutons ensuite du filtrage des données. Même si nous nous concentrons uniquement sur les options avec une date d’expiration d’un mois, nous devons toujours filtrer certains prix obsolètes, c’est-à-dire les prix des options qui ont eu un volume de transactions nul au cours des dernières 24 heures. La liquidité est également un problème clé pour les données sur les contrats à terme à expiration limitée, car les prix à terme obsolètes peuvent entraîner des erreurs dans le calcul du delta de l’option. Par conséquent, nous préférons utiliser la relation de parité call-put (PCP) pour déduire le prix à terme correct plutôt que d’utiliser le prix du marché comme nous le faisons pour les contrats perpétuels très liquides. Si nécessaire, nous filtrons les prix moyens des options qui violent la condition de non-arbitrage proposée par Fengler (2009) et dérivons la volatilité implicite à partir des prix restants. Il convient de noter que la liquidité et l’activité de négociation des options OTM sont beaucoup plus élevées que celles des options ITM avec le même prix d’exercice, nous utilisons donc la volatilité implicite des options de vente pour calculer le cas de m, et utilisons la volatilité implicite des options d’achat. La volatilité est utilisée pour calculer le cas où m ≥ 1. Il est important de noter que la différence entre la volatilité implicite des options d’achat et de vente ATM est presque négligeable. Cela nous permet de créer une grille brute à partir de la surface de volatilité implicite du marché, puis d’interpoler pour obtenir des prix filtrés comme décrit ci-dessous.

Pour obtenir une série historique continue du prix de chaque option, nous construisons les prix de contrats synthétiques à expiration constante de date d’expiration et de propriétés monétaires données. Les options à court terme sont représentées par une date d’expiration fixe de 10 jours, le moyen terme est de 20 jours, tandis que pour le long terme nous considérons une date d’expiration de 30 jours. Étant donné que les prix du Bitcoin subissent souvent des changements de tendance, il est impossible de comparer le même prix d’exercice sur une longue période, nous avons donc également sélectionné une gamme appropriée de propriétés monétaires pour l’interpolation. Nous trouvons un volume important dans une fourchette de prix d’exercice d’environ 30 % au-dessus et en dessous des niveaux du Bitcoin. Par conséquent, nous interpolons les prix des options synthétiques pour chaque échéance constante et propriété monétaire m∈{0,7,0,8,0,9,1,1,1,1,2,1,3} Note 15. En fait, nous utilisons la méthode d’interpolation sur la surface de volatilité implicite sous la limite de non-arbitrage proposée par Fengler (2009), qui propose également une méthode d’interpolation par spline cubique naturelle pour lisser la surface de volatilité implicite. Cependant, la forme de la courbe de volatilité implicite du Bitcoin varie beaucoup plus que celle des autres types d’options, et nous constatons que l’interpolation par spline cubique est trop flexible et sensible aux grands intervalles entre certains prix d’exercice. Par conséquent, nous utilisons des polynômes Hermite cubiques par morceaux préservant la forme pour interpoler la surface de volatilité implicite et vérifier le prix par la suite pour garantir que la contrainte de non-arbitrage de convexité par rapport au prix d’exercice n’est pas violée. Cette technique a été appliquée dans de nombreuses autres études universitaires, telles que Malz (1997) et Bliss et Panigirtzoglou (2002).

Tout d’abord, nous interpolons la courbe de volatilité implicite du sourire pour obtenir une volatilité implicite de monétisation constante sous la restriction de non-arbitrage proposée par Fengler (2009) en utilisant des polynômes Hermite cubiques par morceaux préservant la forme. Ensuite, nous obtenons la volatilité implicite des options à expiration constante et à valeur monétaire constante en interpolant la structure des termes de volatilité et utilisons cette volatilité implicite pour créer des prix d’options synthétiques Note 16. Pour éviter toute possibilité d’arbitrage calendaire, nous veillons à ce que la variance totale implicite augmente avec la date d’expiration. Pour évaluer la performance de couverture, nous devons également enregistrer le prix de chaque option synthétique dans un incrément de temps sans modifier le straddle utilisé pour construire l’option correspondante. Seul ce cadre nous permet d’enregistrer les gains et les pertes d’un portefeuille de couverture dynamique. Nous avons donc créé des contrats à terme et des options synthétiques en utilisant les méthodes qui viennent d’être décrites pour obtenir des prix d’option et de valeur monétaire mis à jour avec des dates d’expiration de 9, 19 et 29 jours pour l’ensemble de données quotidien. De même, dans l’ensemble de données de 8 heures, nous construisons des contrats à terme et des options avec des dates d’expiration de 8 heures inférieures à 10, 20 et 30 jours. Au total, nous avons généré environ 175 000 prix d’options synthétiques à fréquence quotidienne et 88 000 ratios de couverture, ainsi que plus de 525 000 prix d’options synthétiques à fréquence de 8 heures et plus de 263 000 ratios de couverture.

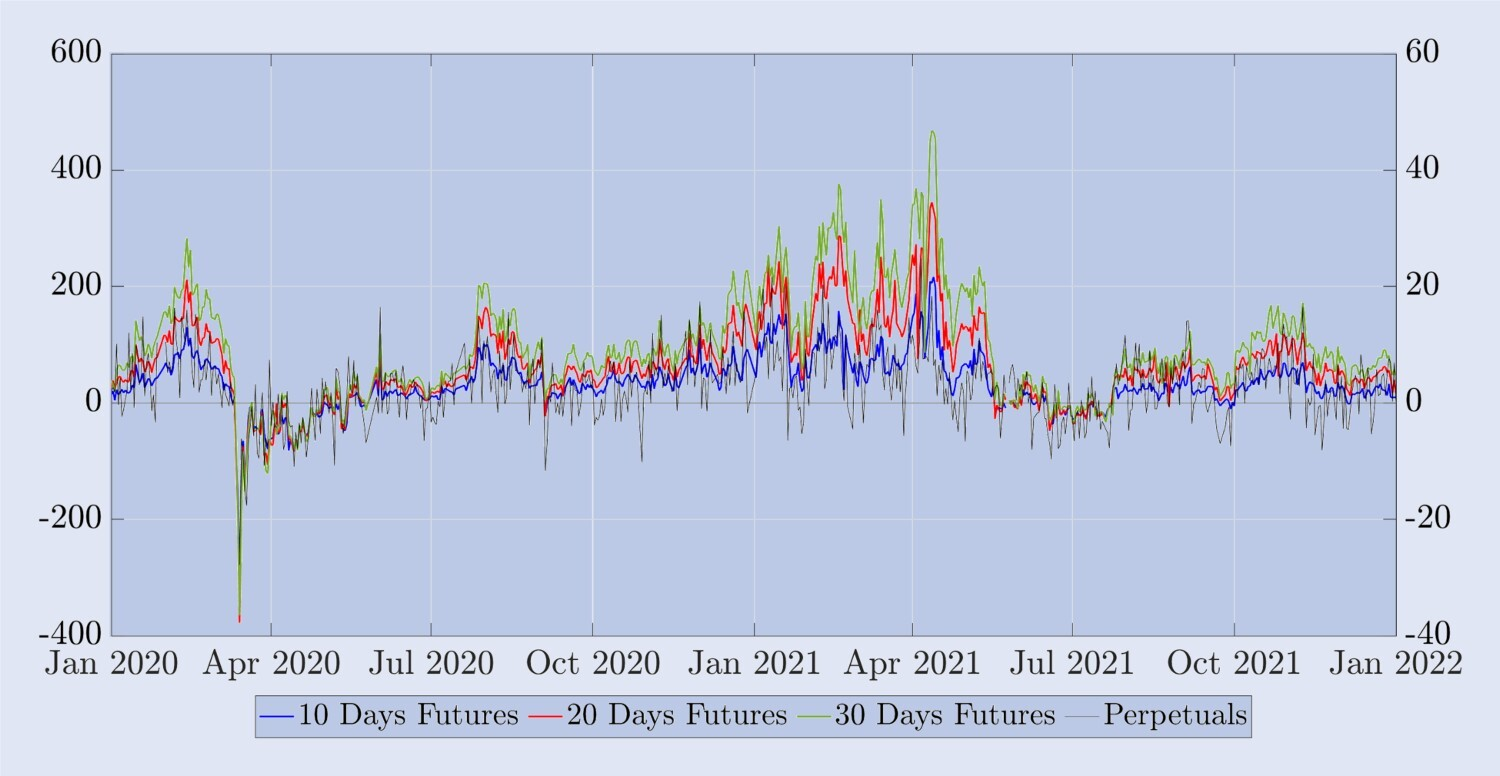
Ensuite, nous examinerons certaines caractéristiques empiriques des contrats perpétuels Bitcoin et les comparerons aux contrats à terme à expiration fixe avant de passer à notre étude de couverture. Le prix de règlement des options Bitcoin n’est pas un contrat négociable, nous devons donc utiliser des contrats à terme ou perpétuels comme outils de couverture. Dans ce cas, l’efficacité de l’utilisation de contrats à terme pour couvrir les options dépend de facteurs tels que la variabilité de la base. Pour illustrer cette variabilité, la figure 7 représente la différence entre le prix du marché à terme (ou contrat perpétuel) et l’indice BTC, divisé par l’indice BTC. Cette base de pourcentage est exprimée en points de base (pb), l’échelle de gauche étant celle des trois contrats à terme synthétiques à échéance fixe et l’échelle de droite étant la base relative au contrat perpétuel. En raison du mécanisme de taux de financement, le risque de base des contrats à terme perpétuels est très faible – moins de ±10 pb la plupart du temps. Mais il est également très volatil : par exemple, lors du krach du COVID en mars 2020, la base perpétuelle a atteint près de -150 pb. Les contrats perpétuels présentent très peu de risque de base, ce qui suggère qu’ils peuvent constituer un meilleur outil de couverture que les contrats à terme calendaires avec la même date d’expiration d’option. Contrairement à la base perpétuelle, la base des contrats à terme à expiration fixe est presque toujours positive. Pour les contrats à terme à 10 jours, la base peut atteindre 100 points de base, tandis que pour les contrats à terme à plus long terme, la base peut même atteindre 450 points de base. De plus, comme on peut le voir sur ce graphique, les courbes des contrats à terme à 10, 20 et 30 jours sont généralement en prime positive - en fait, l’ordre est F30>F20>F10 sur 620 des 730 jours échantillonnés, et uniquement en mars 2020 L’ordre change-t-il ? L’action inverse s’est produite en juin/avril (le krach du COVID et ses conséquences) et en juin/juillet 2021 (la fin de la longue période haussière du Bitcoin).

Figure 7. Différences entre les contrats au comptant et perpétuels et les contrats à terme.

Le prix à terme moins l’indice BTC, divisé par l’indice BTC, exprimé en points de base. L’échelle de droite mesure le pourcentage de base pour les contrats à terme perpétuels (noir) et l’échelle de gauche mesure le pourcentage de base pour les contrats à terme avec des dates d’expiration fixes de 10, 20 et 30 jours (bleu, rouge et vert, respectivement). L’échantillon couvre une période de deux ans commençant en janvier 2020, avec des instantanés quotidiens pris à minuit UTC.

Un autre facteur qui affecte le succès d’une stratégie d’arbitrage delta dynamique sont les coûts de transaction. Si l’écart acheteur-vendeur de l’instrument couvert est important, un rééquilibrage fréquent de l’arbitrage delta (dans notre cas, pas seulement quotidiennement mais toutes les 8 heures) peut éroder la performance de la couverture. Cependant, pour une option donnée, le delta ne peut pas varier entre des valeurs extrêmement différentes, par exemple, une option d’achat proche de la valeur à prix coûtant aura toujours un delta proche de 0,5, quel que soit le modèle utilisé - voir Vähämaa (2004) pour un exemple. exemple. Par conséquent, différentes valeurs delta peuvent avoir un impact significatif sur la performance de la couverture uniquement lorsque l’écart acheteur-vendeur est important. Cependant, les écarts entre les cours acheteur et vendeur sur les contrats à terme perpétuels sont serrés, et même les écarts entre les cours acheteur et vendeur sur les contrats à terme calendaires sont serrés. Pour les contrats à terme perpétuels, l’écart acheteur-vendeur dépasse rarement un tick minimum de 0,50 $, ce qui équivaut à 0,1 à 0,25 point de base, selon le niveau de prix. Les contrats à terme calendaires présentent des écarts acheteur-vendeur légèrement plus importants et augmentent avec la date d’expiration, mais ces écarts sont également très faibles dans notre échantillon. Même pour les contrats à terme à échéance la plus longue, les spreads dépassent rarement 5 points de base et se situent la plupart du temps autour de 1 point de base. Un écart aussi faible a peu d’impact sur nos comparaisons entre différentes valeurs delta, nous l’ignorerons donc dans l’étude empirique suivante.

6. Recherche empirique sur la couverture

Inspirés par notre discussion dans les sections 2, 3 et 5, nous traitons les options inverses comme des options FX classiques, c’est-à-dire que nous utilisons la valeur actuelle de l’option sous-jacente pour convertir son prix Bitcoin en sa valeur USD correspondante. Nous choisissons des dates d’expiration fixes de 10, 20 et 30 jours pour les prix des contrats à terme et des options synthétiques continus, et la valeur monétaire des options est choisie entre 0,7 et 1,3. Nos données sont construites pour des couvertures qui sont rééquilibrées toutes les 8 heures ou quotidiennement, et l’échantillon couvre une période de deux ans du 1er janvier 2020 au 1er janvier 2022, divisée en deux périodes d’un an. Échantillons pour montrer les résultats. A chaque instant t, nous vendons une option européenne de devise m et de date d’expiration T, et la couvrons avec un contrat perpétuel ou un contrat à terme de même date d’expiration que l’option. Les gains et les pertes sont comptabilisés comme des erreurs de couverture en termes physiques, en de la manière habituelle – voir, par exemple, Hull et White (2017). La volatilité du marché intrajournalier peut être très importante et le rééquilibrage entraîne des coûts de transaction très faibles, comme indiqué précédemment. Nous avons donc fixé la fréquence de base du tableau des résultats à toutes les 8 heures. Nous faisons également correspondre le rééquilibrage de 8 heures aux heures de financement des contrats perpétuels, qui sont 00h00, 08h00 et 16h00 UTC. En effet, le rééquilibrage utilisant des contrats perpétuels à des fins de couverture peut également être utilisé pour tirer profit de ses paiements de financement. Note 17

À l’exception du delta HW, tous les deltas de (10) nécessitent que nous calculions la pente de la courbe de volatilité implicite lors du rééquilibrage du portefeuille de couverture. Nous avons étudié diverses techniques numériques pour calculer la dérivée de la courbe de volatilité implicite et avons constaté que l’ajustement d’un polynôme cubique est l’approche la plus simple et la plus précise. Sur la base des valeurs de pente que nous avons calculées numériquement, pour chaque option, en fonction de son potentiel monétaire et de sa date d’expiration, nous appliquons (10) pour calculer le delta et le vega BS en utilisant la formule BS standard. Pour le delta de Hull et White (2017), nous n’imitons pas leur période d’étalonnage de 36 mois dans l’échantillon qu’ils utilisent dans leur travail empirique sur les options sur indices boursiers. Il n’y a même pas 36 mois de données utiles disponibles pour les options Bitcoin. De plus, les prix du Bitcoin sont beaucoup plus volatils que la valeur du S&P 500, c’est pourquoi nous aimerions envisager de nous couvrir plusieurs fois par jour. En tenant compte de tous ces facteurs, nous étalonnons les paramètres delta HW en utilisant 30 fenêtres d’observation à fréquence quotidienne et 90 fenêtres d’observation à fréquence de 8 heures. Nos résultats comparent les erreurs de couverture en utilisant des contrats à terme à expiration fixe et des contrats perpétuels et exécutent deux régressions HW en fonction de l’instrument de couverture.

Nous présenterons nos résultats en utilisant un test F standard des différences de variance, en utilisant le delta BS comme référence, c’est-à-dire le delta Sticky Strike (SS) de (10). Tout d’abord, le tableau 2 présente les résultats de la couverture des options de 7 jours, 1 jour et 3 jours avec des degrés de change compris entre 10,20 et 30,0, où chaque option est couverte avec les contrats à terme à échéance fixe correspondants et rééquilibrée toutes les 8 heures. équilibre. Les entrées du tableau sont des ratios de variance, c’est-à-dire la variance des erreurs couvertes δadj par rapport à la variance des erreurs couvertes delta BS.

Tableau 2. Résultats de couverture du test F (rééquilibrage sur 8 heures, contrats à terme à date d’expiration fixe).

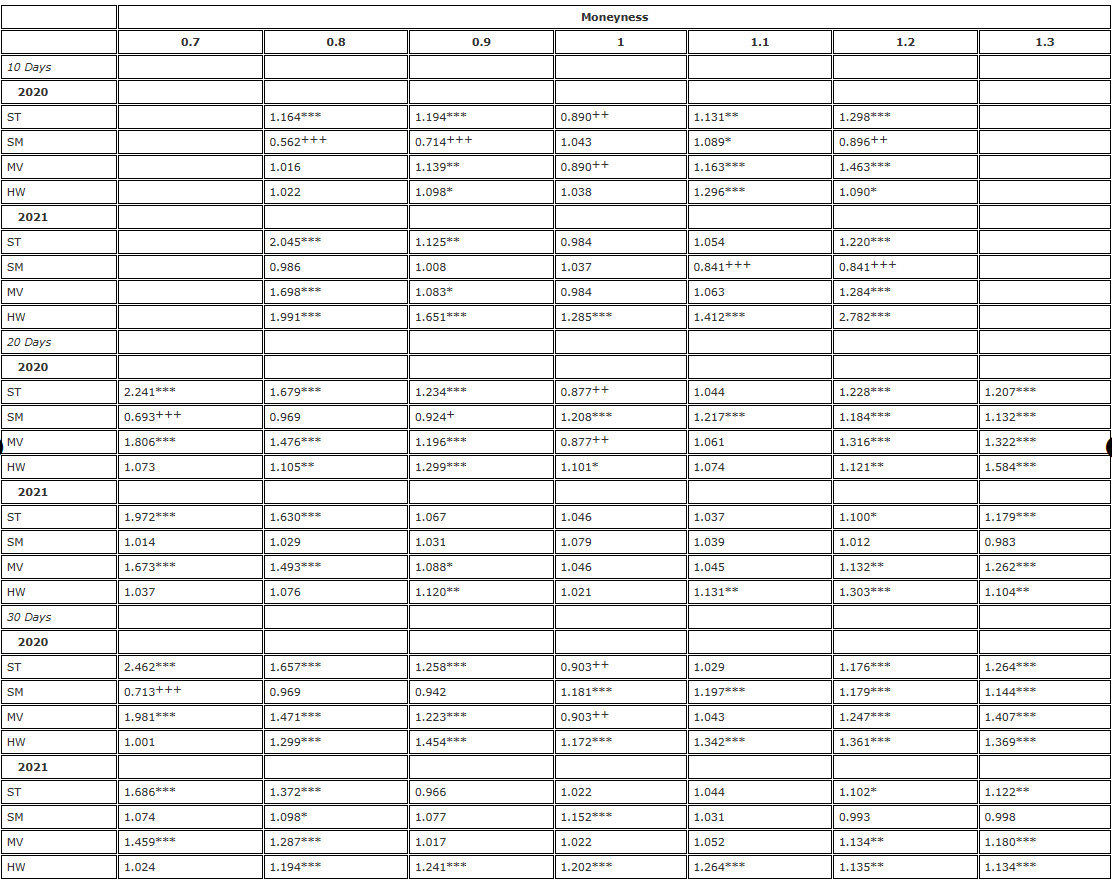
Remarque : Le niveau de signification du rapport de variance et du test F unilatéral concernent respectivement l’hypothèse nulle 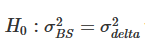et l’hypothèse alternative /upload/asset/28dc6465a12c2e427a5ac.png. La couverture est basée sur un contrat à terme avec la même date d’expiration que l’option et est rééquilibrée toutes les 8 heures. Nous comparons la variance des erreurs provenant de différentes couvertures delta par rapport à la variance provenant de la couverture utilisant le delta BS et divisons l’échantillon de deux ans en deux parties. Nous avons utilisé des options de trois maturités différentes avec un moneyness allant de 0,7 à 1,3, en utilisant des options de vente OTM lorsque le moneyness < 1 et des options d’achat OTM lorsque le moneyness > 1. Pour H∗, , et sont utilisés pour représenter les niveaux de signification de 10 %, 5 % et 1 %, respectivement, et il en va de même pour H+.

Plus l’efficacité de la couverture est grande, plus la variance de l’erreur de couverture est faible et le gain d’efficacité résultant de l’utilisation du delta de la courbe du sourire ajusté est égal à 1 moins ce ratio de variance. Par exemple, lors de la couverture d’une option de 10 jours avec un moneyness de 0,8, le delta SM (Smile Implied) produit un ratio de variance de 0,562. Cela signifie que le gain d’efficacité par rapport à la couverture delta BS est de 1-0,562=43,8%, ce qui est très significatif, donc cette entrée est marquée +++. Dans les tableaux des ratios de variance, les exposants indiquent la signification des ratios de variance aux niveaux de signification de 10 %, 5 % et 1 % dans le test F unilatéral. Par exemple,***Cela indique que la variance de l’erreur de couverture δadj est plus grande que celle de l’erreur de couverture delta BS au niveau de 1 %. Et ++ indique que la variance de l’erreur de couverture δadj est significativement plus petite que l’erreur de couverture delta BS au niveau de 5 %.

Considérons d’abord les résultats de 2020 dans le tableau 2. Cette partie de l’échantillon est caractérisée par des augmentations de prix lentes mais régulières, cohérentes avec le modèle de tendance régulière de Derman (1999), où l’on s’attendrait à ce que le delta SS (delta BS) fournisse la couverture delta la plus efficace, ou dans le cas d’un modèle à portée limitée, le delta SM représente la majorité des deltas. Domination. Dans l’ensemble, les résultats de 2020 présentés dans le tableau 2 montrent un modèle dans lequel le succès d’un delta particulier surperformant une couverture BS dépend de la valeur monétaire de l’option, plutôt que de son échéance. Par exemple, pour les options à prix coûtant, le delta ST fonctionne mieux. Note 18 Les gains d’efficacité obtenus varient de 9,7 % pour l’option à parité de 30 jours à 12,3 % pour l’option de 20 jours et à 11 % pour l’option de 10 jours. La direction relative des performances des deltas implicites du sourire (c’est-à-dire SM) par rapport aux deltas ST et MV est opposée, non seulement pour les options à la monnaie, mais également pour toutes les options dans la monnaie. Il surpasse le delta BS dans la couverture des options de vente OTM, mais pas pour les appels OTM (à l’exception du call à 10 jours avec un moneyness de 1,2). Pour la couverture des options de vente OTM profondes de 20 jours, le gain d’efficacité en utilisant le delta implicite du sourire (SM) tout au long de 2020 est de 1-0,693=30,7%, ce qui est très significatif. Pour les options de vente OTM profondes de 30 jours, le gain d’efficacité est de 28,7 %, ce qui est presque le même. Pour les autres options de vente, les gains d’efficacité résultant de l’utilisation d’une couverture implicite du type « smile » sont bien plus faibles, allant seulement de 3,1 % à 7,6 %.

Cependant, pour toutes les autres options, tous les deltas de sourire ajustés sous-performent le delta BS. Cependant, cela n’est pas surprenant puisque le prix du Bitcoin a suivi une tendance constante pendant une grande partie de l’année 2020. Le ratio de couverture HW actuel proposé par Hull et White (2017) et la couverture de variance minimale (MV) de Lee (2001) n’améliorent pas non plus le delta BS (sauf que pour les options à la monnaie, la couverture MV est la même que ST couverture). L’un des principaux inconvénients du HW delta est qu’il utilise la régression pour estimer ses paramètres, ce qui rend l’hypothèse indépendante et identiquement distribuée invalide pour un actif comme Bitcoin, qui est très sujet aux sauts de rendement. L’impact de tout saut restera dans la fenêtre glissante pendant une longue période et aura donc un impact important sur le ratio de couverture HW.

Les figures 2 et 5 montrent que l’année 2021 a été caractérisée par des prix plus élevés, une plus grande volatilité et une augmentation des niveaux de volatilité globale, couplée à une courbe de volatilité implicite en forme de sourire plus plate, mais toujours asymétrique. Tout au long de l’année 2021, le prix du Bitcoin a fluctué énormément entre 30 000 \( et près de 70 000 \), et comme le montre la figure 2, la courbe du sourire sur 30 jours est devenue relativement plate vers la fin de cette période. Mais la courbe du sourire plate rend le composant clé du delta ajusté, la pente de la courbe du sourire, presque redondant. Il n’est donc pas surprenant qu’au cours de la deuxième année de notre échantillon, tous les deltas ajustés en fonction de la courbe souriante n’apportent pas d’amélioration significative des ratios de couverture BS standard pour toutes les options à 20 et 30 jours. Cependant, en 2021, la courbe du sourire à très court terme de 10 jours a présenté des caractéristiques étranges, avec une tendance à la hausse pendant la phase haussière du prix du Bitcoin. C’est pourquoi la couverture delta implicite Smile (SM) des options d’achat hors de la monnaie à 10 jours montre une amélioration d’efficacité très significative de 15,9 % par rapport à l’utilisation du delta BS.

Ensuite, les tableaux 3 et 4 testent la robustesse des résultats du tableau 2 de deux manières : d’abord en réexécutant l’analyse à une fréquence quotidienne (tableau 3), puis en utilisant des contrats perpétuels au lieu de contrats à terme à échéance identique comme instrument de couverture. . Les résultats du tableau 3 montrent une tendance similaire à ceux du tableau 2, sauf qu’ils sont globalement moins significatifs – mais cela ne devrait pas nous surprendre puisqu’il n’y a désormais que 365 observations par an au lieu de 1 095. Ils confirment notre conclusion du tableau 2 selon laquelle aucune courbe de sourire ajustée delta ne peut améliorer le delta BS en 2021. En 2020, nous avons également observé le même schéma de performance par rapport au delta BS, c’est-à-dire que le delta ST a surperformé BS sur les options ATM, mais il existe désormais des preuves que le delta HW surpasse les options ATM et les options de vente OTM. Il a également surperformé BS avec une moneyness de 0,9 – mais aucune de ces statistiques de rapport de variance n’était statistiquement significative.

Tableau 3. Résultats de couverture du test F (rééquilibrage quotidien, contrats à terme à expiration fixe).

Remarque : Le niveau de signification du rapport de variance et du test F unilatéral concernent respectivement l’hypothèse nulle 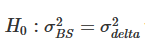et l’hypothèse alternative /upload/asset/28dc6465a12c2e427a5ac.png. La couverture est basée sur un contrat à terme avec la même date d’expiration que l’option et est rééquilibrée toutes les 8 heures. Nous comparons la variance des erreurs provenant de différentes couvertures delta par rapport à la variance provenant de la couverture utilisant le delta BS et divisons l’échantillon de deux ans en deux parties. Nous avons utilisé des options de trois maturités différentes avec un moneyness allant de 0,7 à 1,3, en utilisant des options de vente OTM lorsque le moneyness < 1 et des options d’achat OTM lorsque le moneyness > 1. Pour H∗, , et sont utilisés pour représenter les niveaux de signification de 10 %, 5 % et 1 %, respectivement, et il en va de même pour H+.

Tableau 4. Résultats de couverture du test F (rééquilibrage de 8 heures, contrat perpétuel).

Remarque : Le niveau de signification du rapport de variance et du test F unilatéral concernent respectivement l’hypothèse nulle 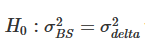et l’hypothèse alternative /upload/asset/28dc6465a12c2e427a5ac.png. La couverture est basée sur un contrat à terme avec la même date d’expiration que l’option et est rééquilibrée toutes les 8 heures. Nous comparons la variance des erreurs provenant de différentes couvertures delta par rapport à la variance provenant de la couverture utilisant le delta BS et divisons l’échantillon de deux ans en deux parties. Nous avons utilisé des options de trois maturités différentes avec un moneyness allant de 0,7 à 1,3, en utilisant des options de vente OTM lorsque le moneyness < 1 et des options d’achat OTM lorsque le moneyness > 1. Pour H∗, , et sont utilisés pour représenter les niveaux de signification de 10 %, 5 % et 1 %, respectivement, et il en va de même pour H+.

Le tableau 4 est exactement le même que le tableau 2, utilisant une fréquence de rééquilibrage de 8 heures pour l’analyse, mais utilisant des contrats perpétuels comme instruments de couverture pour toutes les options. Nous observons exactement le même schéma de sous-performance du delta BS que dans le tableau 2, avec des gains d’efficacité très significatifs pour la couverture des puts OTM en utilisant des deltas ST/MV avec des options delta implicites smile (c’est-à-dire SM) et ATM. À l’exception de la couverture delta implicite de la Smiling Curve (SM) qui a une fois de plus généré un gain d’efficacité important et significatif pour la couverture des options d’achat OTM à 10 jours, aucun delta ajusté de la Smiling Curve n’a pu surpasser de manière significative le delta BS en 2021. Pour les options ATM, il existe également de petits gains d’efficacité (< 5 %) en utilisant le delta ST/MV, et les ratios de variance du tableau 4 sont presque toujours inférieurs à ceux du tableau 2.

Ce constat nous amène à nous demander : les contrats perpétuels constituent-ils un meilleur outil de couverture que les contrats à terme ayant la même échéance que les options ? Pour répondre à cette question, nous examinons le ratio de variance, où le numérateur est la variance de l’erreur de couverture perpétuelle et le dénominateur est la variance de l’erreur de couverture à terme. Nous divisons à nouveau l’échantillon en deux périodes d’un an et présentons les résultats par delta (incluant désormais le delta BS) et par option, et le tableau 5 montre les résultats. Dans le tableau, un ratio de variance inférieur (supérieur à) 1 indique qu’un meilleur (pire) effet de couverture peut être obtenu en utilisant des contrats perpétuels. L’importance de la statistique F dépend du fait que le swap perpétuel offre un outil de couverture meilleur (+) ou pire (-) que les contrats à terme de même échéance.*). Il est clair que le résultat ne dépend presque pas de la valeur monétaire de l’option, mais plutôt de la date d’expiration de l’option et des conditions du marché à ce moment-là. Pour les options à 10 jours, les ratios d’appel OTM sont généralement inférieurs à 1. Pour les options à 20 et 30 jours, la couverture avec des options perpétuelles pourrait connaître des améliorations très significatives, notamment en 2021.

Tableau 5. Test F comparant les contrats à terme et les swaps perpétuels (rééquilibrage toutes les 8 heures).

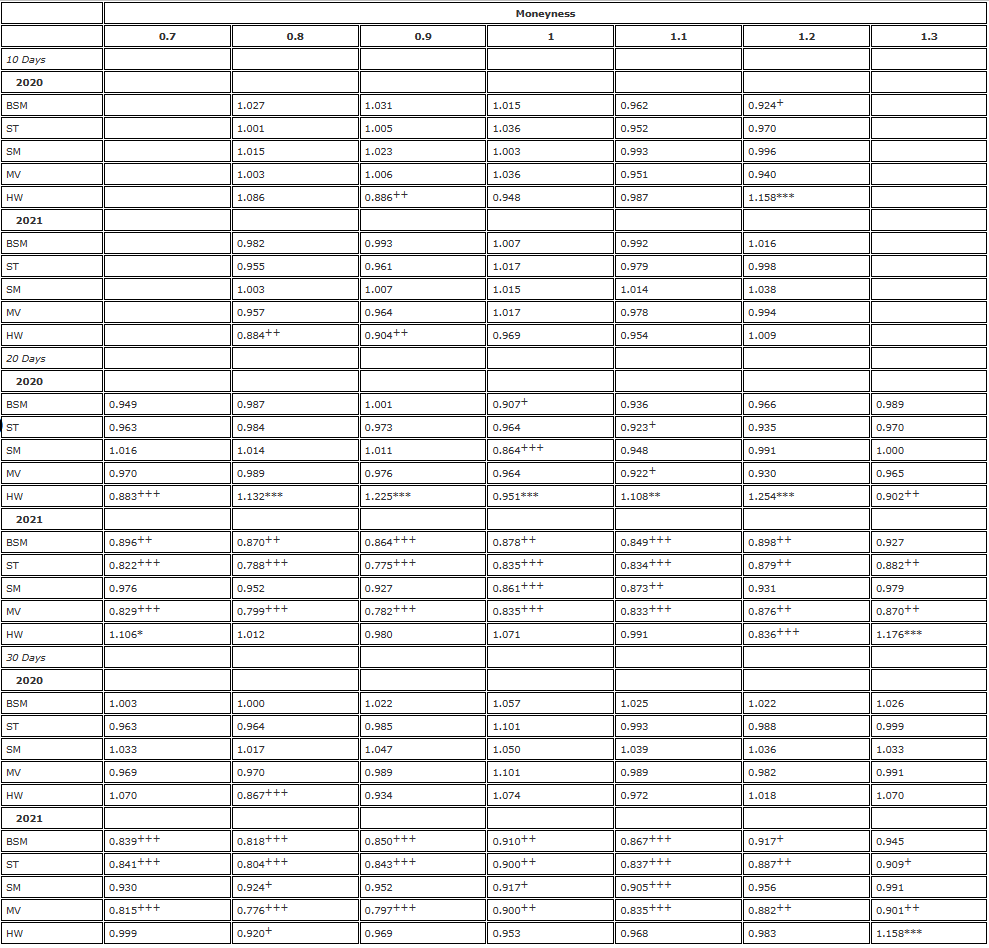
Remarque : Le niveau de signification du rapport de variance et du test F unilatéral concernent respectivement l’hypothèse nulle 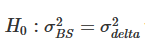et l’hypothèse alternative /upload/asset/28dc6465a12c2e427a5ac.png. La couverture est basée sur un contrat à terme avec la même date d’expiration que l’option et est rééquilibrée toutes les 8 heures. Nous comparons la variance des erreurs provenant de différentes couvertures delta par rapport à la variance provenant de la couverture utilisant le delta BS et divisons l’échantillon de deux ans en deux parties. Nous avons utilisé des options de trois maturités différentes avec un moneyness allant de 0,7 à 1,3, en utilisant des options de vente OTM lorsque le moneyness < 1 et des options d’achat OTM lorsque le moneyness > 1. Pour H∗, , et sont utilisés pour représenter les niveaux de signification de 10 %, 5 % et 1 %, respectivement, et il en va de même pour H+.

Bien que le tableau obtenu fournisse l’efficacité relative globale des deltas par rapport à différents ajustements de la courbe du sourire, notre échantillon de deux ans couvre un large éventail de régimes de marché. Comme le montre la figure 5, le marché du Bitcoin fluctue rapidement entre des tendances stables, des fluctuations de gamme et des baisses et des hausses brutales. Par conséquent, pour aider à comprendre quel delta fonctionne le mieux dans quels états de marché, la figure 8 illustre la série chronologique du ratio de variance, qui est la variance de l’erreur de couverture delta ajustée de la courbe souriante divisée par la variance de l’erreur de couverture delta BS. Il s’agit de rééquilibrer la couverture toutes les 8 heures, et désormais chaque variance est calculée en utilisant uniquement les 90 observations les plus récentes - la même fenêtre utilisée pour l’estimation du paramètre delta HW. Nous soulignons que les valeurs supérieures à 1 indiquent une mauvaise performance de couverture du delta ajusté au sourire par rapport au delta BS. Pour plus de clarté, nous présentons les résultats sur une échelle logarithmique, donc dans ces figures, un rapport de variance de 1 est représenté par zéro . . Toute ligne inférieure à zéro indique que le delta s’améliore par rapport au delta BS, mais une ligne supérieure à zéro montre que le delta fournit une couverture moins efficace que le BS.

Figure 8. Performance de couverture de l’échantillon roulant. (a) Résultats des options sur 10 jours et (b) Résultats des options sur 30 jours.

Le ratio de variance montre comment différents ratios de couverture d’options perpétuelles se comportent par rapport au delta BS en utilisant un rééquilibrage de 8 heures, où la variance de l’erreur de couverture est calculée à l’aide des 90 premières observations. Nous présentons les résultats du journal pour (a) les options de 10 jours et (b) les options de 30 jours sur un échantillon de deux ans. La ligne continue 0 est une valeur de référence, un ratio supérieur à 0 indique une performance inférieure à BS, et un ratio inférieur à 0 indique une meilleure performance par rapport à BS. La figure (a) ci-dessus illustre la performance d’une option de vente OTM avec m=0,8, tandis que le graphique supérieur de (b) montre la performance d’une option de vente OTM avec m=0,7. Le graphique du milieu montre la performance de (a) et (b). Les performances des options ATM sont présentées ci-dessous pour les options d’achat OTM avec (a) un moneyness de 1,2 et (b) un moneyness de 1,3.

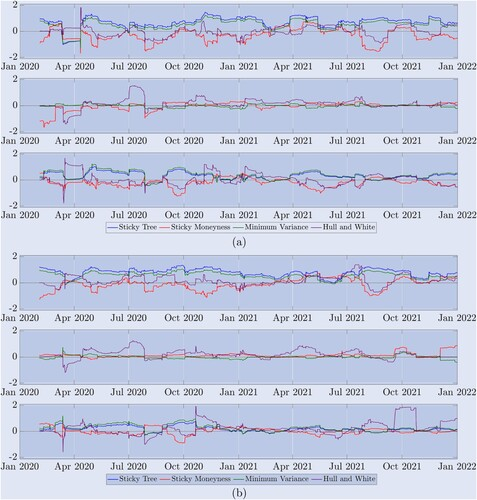
Les trois graphiques supérieurs (a) montrent les résultats pour les options sur 10 jours, et les trois graphiques inférieurs (b) montrent les résultats pour les options sur 30 jours. Dans chaque cas (a) et (b), les graphiques ci-dessus concernent les options de vente OTM. Ces graphiques confirment les résultats du tableau 2 : les deltas de ST (bleu) et MV (vert) ont sous-performé sur presque toute la période. que BS ; selon les attentes de classification du marché de Derman (1999), le delta SM surpasse le delta BS pendant les périodes où le marché est dans une fourchette, mais lorsque le marché est en tendance, comme la première période commençant en janvier 2021, pendant la deuxième Lors de la course haussière et de la deuxième course haussière plus tard cette année-là, le delta SM n’a pas eu d’aussi bons résultats que le delta BS ; tandis que le delta HW a eu des résultats différents. Le graphique du milieu de chaque ensemble de graphiques montre le ratio de variance des options ATM couvertes. Dans ce cas, tous les deltas ajustés au sourire sont très similaires, car le sourire de Bitcoin est généralement (mais pas toujours) très plat à ce stade. Le graphique du bas de chaque ensemble de graphiques montre les performances de différents deltas pour la couverture des options d’achat OTM. Encore une fois, le SM delta semble être la meilleure option, mais il n’est disponible que pour les options de 10 jours et ne constitue pas une amélioration aussi importante par rapport à BS que l’a déclaré l’OTM. Pour les options à 30 jours, aucun delta n’a été en mesure d’améliorer systématiquement les BS, en particulier en 2021.

7. Conclusion

Les études empiriques universitaires antérieures n’ont examiné que la couverture delta avec une courbe souriante implicite sans modèle et une courbe souriante dépendante de l’institution ajustée pour les options sur indices boursiers. Bien que les résultats soient mitigés, la conclusion générale est qu’un ratio de couverture ajusté en fonction de la courbe souriante ne peut qu’améliorer la performance du delta Black-Scholes pour les options de vente hors de la monnaie dans certaines circonstances. Mais nous avons démontré que la courbe du sourire de volatilité implicite du Bitcoin se comporte très différemment des options sur indices boursiers, il est donc très intéressant d’étudier l’efficacité du ratio de couverture ajusté à la courbe du sourire que les praticiens privilégient généralement.

Nous encourageons l’utilisation de diverses utilisations potentielles du delta ajusté, dont la plupart reposent uniquement sur la relation entre la volatilité implicite de l’option de couverture et la pente de la courbe de volatilité implicite du sourire au moment de l’expiration. En utilisant un ensemble de données unique sur les options Deribit, nous sommes en mesure de comparer les performances de couverture des options Bitcoin les plus actives sur la bourse Deribit, c’est-à-dire des options avec des prix d’exercice 30 % supérieurs et inférieurs à l’indice BTC actuel et des délais d’expiration allant jusqu’à un mois. Nous analysons la variance des erreurs de couverture delta, où l’instrument de couverture peut être un contrat à terme avec la même date d’expiration que l’option ou un contrat perpétuel - un produit innovant unique au marché des dérivés de crypto-monnaie. En rééquilibrant la couverture toutes les huit heures (coïncidant avec le temps de financement du contrat perpétuel) ou quotidiennement, et en utilisant des contrats à terme ou des contrats perpétuels avec le même temps d’expiration que l’instrument de couverture, nous obtenons des résultats très robustes. De plus, plutôt que de simplement tabuler les erreurs quadratiques moyennes de différents ratios de couverture comme l’ont fait Coleman et al. (2001), Vähämaa (2004), Alexander et al. (2012) et bien d’autres, nous appliquons un simple test de ratio de variance. qui fournit la signification statistique du gain d’efficacité de l’utilisation d’un delta donné par rapport au delta BS.

En utilisant cette approche, nous démontrons que pour les options hors de la monnaie, le delta implicite de la courbe souriante (sticky moneyness) est significativement meilleur que le delta Black-Scholes standard en matière de couverture, dans certains cas de plus de 40 % plus efficacement . Le delta de variance minimum surpasse également le delta BS, mais uniquement pour les options in-the-money, car il coïncide avec le delta de l’arbre collant. Aucun autre delta ajusté par la courbe souriante ne s’est systématiquement amélioré par rapport au delta BS, et même les couvertures delta implicites par le sourire et à variance minimale ont eu de mauvais résultats pendant une grande partie de 2021. La seule exception est la couverture implicite du sourire sur les options d’achat à court terme hors de la monnaie lorsque la pente de la courbe de volatilité implicite devient positive. Comparé aux indices boursiers comme le S&P 500, les prix du Bitcoin ne fluctuent pas à la hausse de manière constante pour ensuite s’effondrer soudainement - ses augmentations de prix peuvent être aussi importantes que ses baisses de prix, de sorte que sa courbe du sourire peut être très symétrique ou même complètement inclinée vers le haut. . Nous démontrons également que les contrats perpétuels sont de meilleurs instruments de couverture que les contrats à terme ayant la même maturité que les options, quelle que soit la valeur monétaire des options. Cela est particulièrement évident dans le cas des options à plus long terme, où la base entre les contrats perpétuels et les contrats à terme est la plus grande.

Nos recherches se concentrent sur des cadres robustes sans modèle, qui sont également le choix préféré de nombreux praticiens. Nous n’envisageons pas de couverture à l’aide de modèles stochastiques paramétriques et/ou de volatilité locale pour la simple raison que l’invariance d’échelle de ces processus signifie que le delta est effectivement sans modèle et coïncide donc avec le delta implicite du sourire utilisé dans cette étude. Étant donné que nous introduisons le delta de variance minimale robuste de Lee (2001) dans notre étude, nous pensons que l’ajout de différents processus de volatilité stochastique pour la couverture delta dynamique est une question de recherche moins pertinente pour l’industrie actuelle du trading de crypto-monnaies.

Cet article se concentre sur la couverture delta dynamique avec rééquilibrage fréquent, ce qui peut aider les teneurs de marché des options Bitcoin à obtenir un avantage concurrentiel sur un marché qui ne commence vraiment à mûrir qu’en 2021. Cependant, le marché du Bitcoin a connu une croissance si rapide que de grands traders professionnels comme Jump Trading, Jane Street, XBTO et Cumberland DRW négocient des options Bitcoin, souvent avec des volumes quotidiens dépassant 1 milliard de dollars. De nombreuses nouvelles options d’expiration et tailles de contrats d’options sont également introduites pour répondre à la demande. Par exemple, CME a récemment lancé des options micro Bitcoin pour les traders de détail. Malgré cela, l’écart entre les cours acheteur et vendeur des options Bitcoin reste relativement important, bien supérieur à celui des contrats à terme ou perpétuels Bitcoin. Par conséquent, la rentabilité du market making sur le marché des options Bitcoin repose davantage sur une couverture delta dynamique précise que sur une couverture delta-gamma-vega. Si le spread bid-ask des options Bitcoin diminue à l’avenir, il peut être intéressant d’étudier la couverture gamma et vega du carnet d’options Bitcoin. Cependant, au moment de la rédaction du présent document, les coûts de transaction liés à l’utilisation d’options pour couvrir les risques de prix et de volatilité peuvent éroder les bénéfices supplémentaires qui pourraient être réalisés grâce à des spreads plus faibles.

déclaration

Nous remercions les évaluateurs anonymes dont les commentaires ont considérablement amélioré l’article.

Déclaration de divulgation

Les auteurs déclarent ne pas avoir de conflits d’intérêts.

Remarques

1. En revanche, les deltas dérivés de modèles non invariants d’échelle, tels que le modèle de volatilité locale de Dupire (1994) ou le modèle d’arbre collant de Derman et Kани (1994), ne sont pas théoriquement équivalents aux deltas invariants d’échelle. La variance minimale Delta n’est pas non plus un Delta invariant d’échelle, c’est la dérivée totale qui inclut l’effet Vega des corrélations de volatilité des prix non nulles.

2. Par exemple, voir le récentArticles de la CAIA, un autre article sur mediumarticle,ainsi que risklatte et stackexchange Et plusieurs forums de finance quantitative.

3. Dans cette littérature, Nastasi et al. (2020) calibrent un modèle de cohérence du sourire pour les options sur matières premières afin de capturer la dynamique du sourire, tandis que Malz (2000) explique comment prendre en compte les ajustements du sourire lors de la mesure du risque des options de change. À l’intérieur.

4. Les options Deribit ont une expiration biquotidienne, bihebdomadaire, bimensuelle et trimestrielle, et peuvent durer jusqu’à 9 ou 12 mois. Son actif sous-jacent est le « Deribit BTC Index » (BTC), qui est une moyenne pondérée de manière égale des derniers prix du Bitcoin sur 11 bourses, excluant les prix les plus élevés et les plus bas. Les 9 prix restants sont utilisés pour calculer l’indice. Actuellement, ces échanges incluent Binance, Bitfinex, Bitstamp, Bittrex, Coinbase Pro, Gemini, Huobi Global, Itbit, Kraken, LMAX Digital et OKEx, et l’indice est mis à jour toutes les secondes. Il existe plus de dates d’expiration d’options que de dates d’expiration de contrats à terme. Ainsi, pour que Deribit puisse répertorier les prix des options pour Bitcoin et USD, ils utilisent les mêmes prix à terme (éventuellement synthétiques) que les dates d’expiration des options. Cela ne signifie pas que le contrat à terme (éventuellement synthétique) est le sous-jacent. En fait,Spécifications des options de Deribit Il est clairement indiqué que l’actif sous-jacent est l’indice Deribit BTC. Pour les options à court terme, la plage d’exercice varie de 50 % à 150 % du prix actuel du BTC, et pour les options avec des échéances supérieures à 6 mois, la plage d’exercice peut atteindre 800 % du prix actuel du BTC.

5. Voir aussiDonnées historiques sur les options du CBOE, pour comprendre le volume de négociation des options SPX sur CBOE.

6. Voir aussiVolume de négociation des options Bitcoinet Options Bitcoin de Goldman Sachs。

7. Viennent ensuite CME (5 %), puis OKEx (2,5 %), puis FTX et Bit.com, voirThe Block Options。

8. Pour calculer le rendement final, Deribit utilise l’indice BTC moyen 30 minutes avant l’expiration comme valeur de règlement. Pour plus de détails, consultez le site officielSpécifications des options de Deribit . Il est important de noter que le marché des options Bitcoin de Deribit n’est pas complet. Les indices eux-mêmes ne sont pas négociables et nécessitent une réplication coûteuse et un rééquilibrage fréquent. Le marché est incomplet pour les traders en raison du manque d’informations sur le calcul précis de la valeur de règlement. Cependant, une discussion détaillée de cette question dépasse le cadre de cet article, et nous renvoyons à Alexander et al. (2022a) pour une discussion approfondie.

9. Veuillez vous référer à 2022Marché décentralisé des crypto-monnaies Classement.

10. Les contrats à terme inverses sont des contrats à terme libellés en Bitcoin basés sur le prix en USD du Bitcoin ou sur la valeur d’un indice Bitcoin. Les contrats à terme standard et inverse utilisent tous deux la valeur USD comme valeur sous-jacente, mais ils diffèrent dans la méthode de règlement : les contrats à terme standard du CME ont un montant notionnel de 0,1 ou 5 bitcoins et sont payés en USD, tandis que le montant notionnel des contrats à terme inverses est de 1 \( ou 10 \). , et payable en Bitcoin. En revanche, ce mécanisme de paiement conduit à un calcul de profits et pertes (PnL) différent. Pour les contrats à terme standard, vous devez soustraire le prix de clôture du prix d’ouverture du contrat à terme et multiplier le résultat par le montant notionnel pour obtenir le profit ou la perte en dollars américains. Les contrats à terme inverses (et les options) ont une procédure de règlement différente, qui prend l’inverse du prix d’ouverture moins l’inverse du prix de clôture, puis multiplie le résultat par le montant notionnel de la position pour obtenir le profit ou la perte mesuré en Bitcoin. Le « prix d’ouverture » et le « prix de clôture » font ici référence à la valeur en dollars du contrat à terme au moment de l’entrée et de la sortie de la position.

11. Voir aussiTaux de financement perpétuel de Deribit, pour une description du calcul du taux de financement de Deribit.

12. Voir aussiThe BlockouCoinglass. Il est important de noter que plus de huit bourses ont affiché des volumes de transactions anormalement élevés. Cependant, nous avons négligé les nombreuses bourses qui avaient artificiellement gonflé leurs volumes en raison du wash trading.

13. Cette approximation a également été préconisée par Coleman et al. (2001) et bien d’autres.

14. Derman (1999) a qualifié le modèle SS de « tentative du pauvre » de reproduire le modèle BS en utilisant un arbre de volatilité implicite.

15. À l’exception des options de vente (m=0,7) et des options d’achat (m=1,3) très hors de la monnaie, ces options sont sous-négociées dans la catégorie des expirations à court terme. Nous n’avons pu calculer les prix synthétiques que 75 % du temps, nous avons donc exclu ces options de nos résultats finaux.

16. Bien entendu, la valeur PCP pour chaque niveau d’exercice sera différente. Étant donné que les échanges sont généralement concentrés sur les options ATM, il est difficile de trouver un niveau d’exercice ITM/OTM où les appels et les puts sont activement négociés, nous utilisons donc la valeur PCP dérivée du rétrocalcul des options ATM. Nous interpolons les valeurs ATM PCP pour deux dates d’expiration adjacentes et utilisons ces valeurs pour obtenir des prix d’options fixes synthétiques si nécessaire.

17. Par exemple, étant donné que nous détenons toujours un contrat perpétuel dans notre construction, l’opérateur de couverture doit payer un financement lorsque la base du contrat perpétuel est positive et reçoit un financement lorsque la base est négative. L’inverse est vrai pour la couverture des positions d’options longues. En tout cas, à partir de la figure 7, nous pouvons voir que la base du contrat perpétuel est en train de changer, parfois positivement et parfois négativement. Il n’est pas difficile d’écrire un algorithme de couverture pour sortir complètement d’une position couverte avant l’expiration du financement, mais il ne sortira pas si la position couverte reçoit un financement. Ce type de « stratégie de frais de financement » est très courant aujourd’hui parmi les hedge funds, sur des marchés où il n’existe aucune réglementation empêchant ces robots de trading st