Une stratégie de négociation intraday utilisant la régression de l'égalité entre SPY et IWM

Dans cet article, nous allons écrire une stratégie de négociation intraday. Elle utilisera le concept classique de négociation, qui consiste à négocier des paires de titres par rapport à la valeur de l'argent. Dans cet exemple, nous allons utiliser deux fonds d'indices ouverts (ETF), SPY et IWM, qui sont négociés sur le NYSE et tentent de représenter les indices boursiers américains, respectivement le S&P 500 et le Russell 2000.

La stratégie consiste à créer un écart de rentabilité en faisant plusieurs ETF et en faisant un autre ETF vide. Le poly-écart peut être défini de plusieurs manières, par exemple en utilisant une méthode de séquence de temps de synchronisation statistique. Dans ce scénario, nous calculerons le ratio de couverture entre SPY et IWM en utilisant une régression linéaire en rotation. Cela nous permettra de créer un écart de rentabilité entre SPY et IWM, qui est normalisé en z-score.

Le principe de base de cette stratégie est que SPY et IWM représentent à peu près la même situation du marché, c'est-à-dire la performance des actions d'un groupe de grandes et de petites entreprises américaines. L'hypothèse est que, si l'on accepte la théorie de la régression de l'équilibre des prix, il y a toujours une régression, car les événements d'équilibre peuvent affecter le S&P 500 et le Russell 2000 respectivement dans un court laps de temps, mais les écarts de profit entre eux reviennent toujours à une moyenne normale, et les deux séquences de prix à long terme sont généralement cointégrées.

La stratégie

La stratégie est exécutée en suivant les étapes suivantes:

Données - 1 minute de k-string obtenu par SPY et IWM, respectivement, d'avril 2007 à février 2014.

Traiter - aligner correctement les données et supprimer les k-strings qui manquent les uns des autres.

Différence - Le ratio de couverture entre les deux ETFs est calculé à l'aide d'un calcul de régression linéaire en rotation. Défini comme le coefficient de régression β en utilisant une fenêtre de régression qui déplace 1 ligne k vers l'avant et recalcule le coefficient de régression.

Z-Score - La valeur du décalage standard est calculée de la manière habituelle. Cela signifie soustraire la valeur moyenne du décalage standard à l'échantillon et enlever le décalage standard à l'échantillon. La raison de ce fait est de rendre les paramètres de seuil plus faciles à comprendre, car le Z-Score est une quantité sans dimension.

Traitements - lorsque le z-score négatif tombe en dessous du seuil prévu (ou post-optimisé), un signal de plus est généré, tandis que le signal de moins en est le contraire. Lorsque le z-score absolue tombe en dessous du seuil supplémentaire, un signal de mise à l'échelle est généré. Pour cette stratégie, j'ai (un peu au hasard) choisi z = 2 comme seuil d'ouverture et z = 1 comme seuil de mise à l'échelle.

Peut-être que la meilleure façon d'approfondir la compréhension de la stratégie est de l'implémenter concrètement. La section suivante présente en détail le code Python complet (un seul fichier) utilisé pour implémenter cette stratégie de retour d'égalité. J'ai ajouté des notes de code détaillées pour vous aider à mieux comprendre.

Mise en œuvre de Python

Comme tous les tutoriels Python/pandas, il faut les configurer selon l'environnement Python décrit dans ce tutoriel. Une fois la configuration terminée, la première tâche est d'importer la bibliothèque Python nécessaire.

Les versions spécifiques que j'utilise sont les suivantes:

Python - 2.7.3 NumPy - 1.8.0 Les pandas - 0.12.0 Le projet de loi est en cours de révision.

Nous allons continuer et importer les bibliothèques suivantes:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

La fonction suivante create_pairs_dataframe importe deux fichiers CSV de k lignes interne contenant deux symboles. Dans notre exemple, ce sera SPY et IWM. Elle crée ensuite une paire de données de paire de paires séparée, qui utilisera l'index des deux fichiers d'origine. Leurs délais peuvent varier en raison de transactions manquées et d'erreurs.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

L'étape suivante consiste à effectuer une régression linéaire en rotation entre SPY et IWM. Dans ce scénario, IWM est le prédicteur (x) et SPY est la réponse (y). J'ai mis en place une fenêtre de régression par défaut de 100 lignes k. Comme indiqué ci-dessus, il s'agit des paramètres de la stratégie. Pour que la stratégie soit considérée comme solide, nous souhaitons idéalement voir un rapport de retour afficher un état de fonction concave (x) ou une autre performance métrologique au cours de la régression.

Après avoir calculé le coefficient de rotation β dans le modèle de régression linéaire SPY-IWM, on l'ajoute à la paire DataFrame et on supprime les lignes vierges. Cela construit le premier groupe de lignes K, qui est égal à une mesure de retouche de longueur rétroactive. Ensuite, on crée deux écarts d'ETF, les unités de SPY et les unités de -βi de IWM. Évidemment, ce n'est pas réaliste, car nous utilisons une petite quantité d'IWM, ce qui est impossible dans la mise en œuvre réelle.

Enfin, nous créons le z-score du décalage d'intérêt, calculé en soustrayant la moyenne du décalage d'intérêt et en utilisant le décalage standard du décalage d'intérêt standardisé. Il convient de noter qu'il existe un décalage de perspective assez subtil. Je l'ai intentionnellement laissé dans le code parce que je voulais souligner à quel point il est facile de commettre de telles erreurs dans les études.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Dans create_long_short_market_signals, créer des signaux de négociation. Ceux-ci sont calculés par une valeur de z-score supérieure au seuil.

Pour ce faire, il est nécessaire d'établir une stratégie de transaction pour chaque ligne k: ouvrir le coffre ou fermer le coffre. Long_market et short_market sont les deux variables définies pour suivre les positions multi-tête et blanche. Malheureusement, il est plus facile de programmer de manière irrégulière que la méthode de quantification, ce qui rend le calcul plus lent. Bien que les cartes de ligne de 1 minute nécessitent environ 700 000 points de données par fichier CSV, le calcul est encore relativement rapide sur mon ancien bureau!

Il est nécessaire d'utiliser la méthode iterrows, qui fournit un générateur d'itération:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

À ce stade, nous avons mis à jour les paires pour qu'elles incluent des signaux multiples et vides réels, ce qui nous a permis de déterminer si nous devions ou non ouvrir une position. Maintenant, nous devons créer un portefeuille pour suivre la valeur marchande des positions. La première tâche consiste à créer une colonne de positions combinant les signaux multiples et les signaux vides.

Une fois la valeur marchande de l'ETF créée, nous les combinons pour produire une valeur marchande totale à la fin de chaque ligne k. Ensuite, nous la convertissons en valeur de retour via la méthode pct_change de cet objet. Les lignes de code suivantes nettoient les entrées incorrectes (NaN et les éléments inf) et finissent par calculer la courbe d'intérêt complète.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Les fonctions principales les combinent. Le fichier CSV interne est situé dans le chemin datadir. Veuillez modifier le code ci-dessous pour qu'il pointe vers votre répertoire spécifique.

Pour déterminer la sensibilité de la stratégie aux cycles de lookback, il est nécessaire de calculer une série d'indicateurs de performance de lookback. J'ai choisi le pourcentage de rendement total final du portefeuille comme indicateur de performance et la plage de lookback[50,200], en multiples de 10. Vous pouvez voir dans le code ci-dessous que la fonction précédente est incluse dans le cycle for de cette plage, les autres seuils restant inchangés.

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

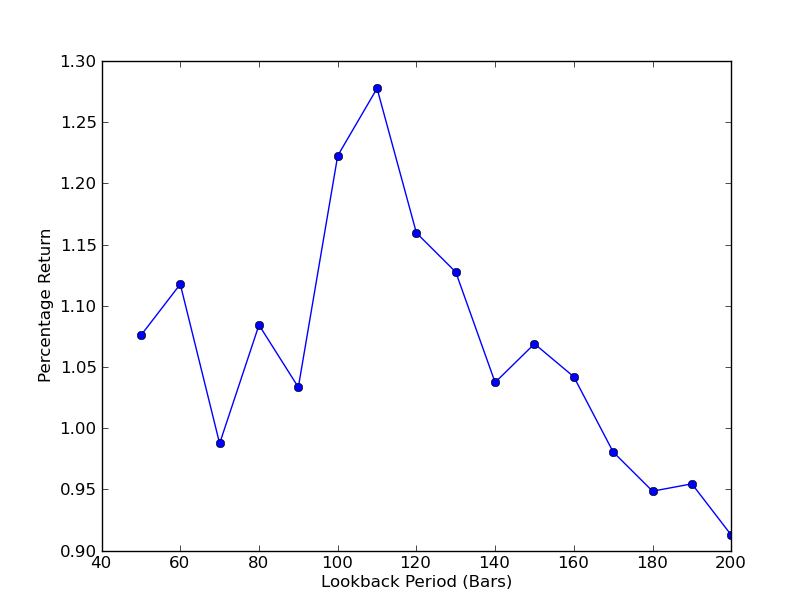
On peut maintenant voir le graphique des lookbacks et des retours. Notez que lookback a une valeur maximale de lookback globale, égale à 110 k-lines. Si nous voyons que les lookbacks ne sont pas liés aux retours, c'est parce que:

SPY-IWM analyse de la sensibilité à la période de rétrogradation linéaire par rapport à la période de rétrogradation

Aucun article de rétrospective n'est complet sans une courbe de profit inclinée vers le haut! Par conséquent, si vous souhaitez tracer une courbe de rendement cumulatif des bénéfices par rapport au temps, vous pouvez utiliser le code suivant. Il tracera le portefeuille final généré à partir de l'étude des paramètres de lookback. Il est donc nécessaire de choisir un lookback en fonction du graphique que vous souhaitez visualiser.

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

Le graphique suivant de la courbe des droits et intérêts a une période de rétrospective de 100 jours:

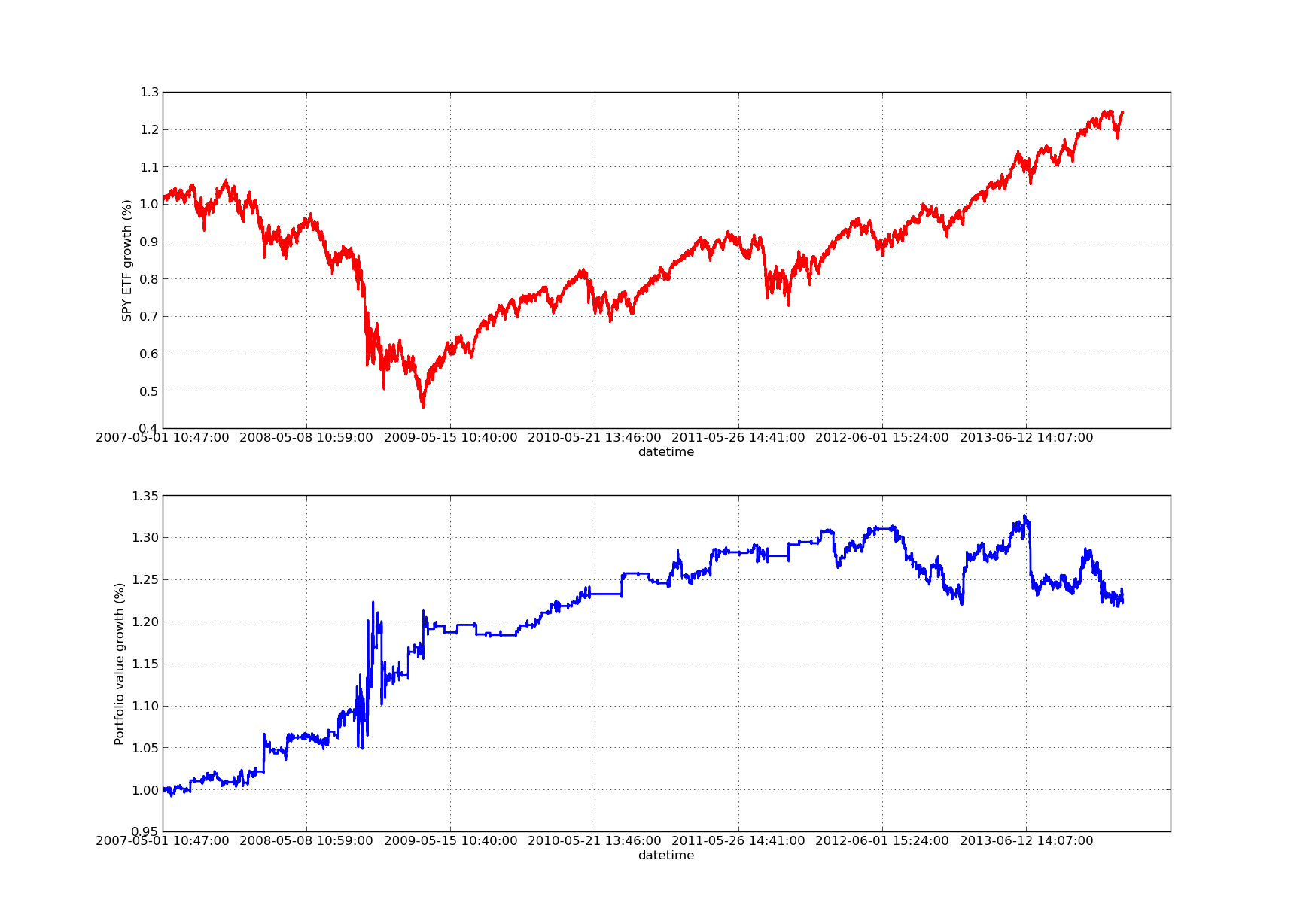
SPY-IWM analyse de la sensibilité à la période de rétrogradation linéaire par rapport à la période de rétrogradation

Veuillez noter que le SPY a connu une forte contraction en 2009 pendant la crise financière. La stratégie est également en période de turbulence à ce stade. Veuillez également noter que la performance de l'année dernière s'est détériorée en raison de la nature fortement tendancielle du SPY pendant cette période, ce qui reflète l'indice S&P 500.

Veuillez noter que nous devons toujours prendre en compte l'écart d'optimisation de l'effet de levier lorsque nous calculons le z-score. De plus, tous ces calculs ont été effectués sans frais de transaction. Une fois que ces facteurs sont pris en compte, cette stratégie est sûre de mal fonctionner. Les frais de traitement et les points de glissement ne sont pas encore définis.

Dans un article ultérieur, nous allons créer un backtester événement-driven plus sophistiqué qui tiendra compte de ces facteurs et nous donnera plus de confiance dans la courbe de financement et les indicateurs de performance.