क्या आप एसवीएम वेक्टर मशीनों के साथ दांव लगाकर (व्यापार करके) गोरिल्लाओं से आगे निकल सकते हैं?

देवियो और सज्जनों, अपने दांव लगाओ। आज, हम एक ओरिगामी को हराने के लिए अपना सर्वश्रेष्ठ प्रयास करेंगे, जिसे वित्तीय क्षेत्र में सबसे भयानक प्रतिद्वंद्वियों में से एक माना जाता है।
मैं आपको विश्वास दिलाता हूं, यहां तक कि एक यादृच्छिक बाजी मारना और 50% जीतने की संभावना वाला एक गिलहरी भी एक कठिन काम है।
हम एक तैयार मशीन सीखने एल्गोरिथ्म का उपयोग करेंगे जो वेक्टर वर्गीकरण का समर्थन करता है। एसवीएम वेक्टर मशीन एक अविश्वसनीय रूप से शक्तिशाली विधि है जो रिग्रेशन और वर्गीकरण कार्यों को हल करने के लिए है।

• SVM समर्थित वेक्टर

एसवीएम वेक्टर मशीन इस विचार पर आधारित है कि हम p-वर्ग विशेषताओं के लिए सुपरप्लेन स्पेस का उपयोग कर वर्गीकरण कर सकते हैं। एसवीएम वेक्टर मशीन एल्गोरिथ्म एक सुपरप्लेन और एक पहचान मार्जिन का उपयोग करता है वर्गीकरण निर्णय सीमा बनाने के लिए, जैसा कि नीचे दिखाया गया है।

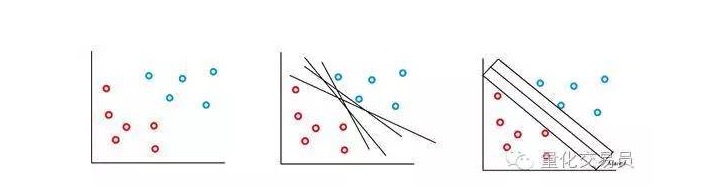
सबसे सरल स्थिति में, रैखिक वर्गीकरण संभव है। एल्गोरिदम ने निर्णय सीमा का चयन किया है, जो कक्षाओं के बीच की दूरी को अधिकतम कर सकता है।

अधिकांश वित्तीय समय-क्रमों में, आपको सरल, रैखिक रूप से अलग-अलग सेटों का सामना करने की संभावना नहीं है, लेकिन अक्सर ऐसा होता है कि वे अलग-अलग नहीं होते हैं। एसवीएम वेक्टर मशीन ने इस समस्या को हल करने के लिए एक विधि लागू की है जिसे सॉफ्ट मार्जिन विधि कहा जाता है।

इस मामले में, कुछ गलत वर्गीकरण की स्थिति की अनुमति है, लेकिन वे स्वयं फ़ंक्शन को निष्पादित करते हैं ताकि सी के साथ सकारात्मक अनुपात हो सके (लागत या बजट की त्रुटि की अनुमति दी जा सकती है) और सीमा से त्रुटि की दूरी को कम से कम करने के लिए।

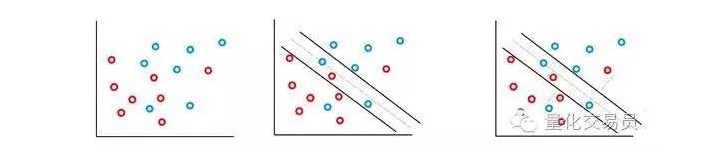
मूल रूप से, मशीन वर्गीकरण के बीच की दूरी को अधिकतम करने की कोशिश करती है और अपने C-भारित दंड को कम करने की कोशिश करती है।

एसवीएम वर्गीकरणकर्ता की एक अच्छी विशेषता यह है कि वर्गीकरण निर्णय सीमा का स्थान और आकार केवल उस डेटा के एक हिस्से द्वारा निर्धारित किया जाता है जो निर्णय सीमा से निकटतम है। इस तरह के एल्गोरिथ्म की विशेषताएं इसे दूर-दूर के असामान्य मानों के हस्तक्षेप का मुकाबला करने में सक्षम बनाती हैं। उदाहरण के लिए, ऊपर दिए गए आरेख में, सबसे दाईं ओर नीला बिंदु, निर्णय सीमा पर बहुत कम प्रभाव डालता है।

क्या यह बहुत जटिल है? ठीक है, मुझे लगता है कि मज़ा अभी शुरू हुआ है।

निम्नलिखित परिस्थितियों पर विचार करें (रेड डॉट्स को अन्य रंगों से अलग करें):

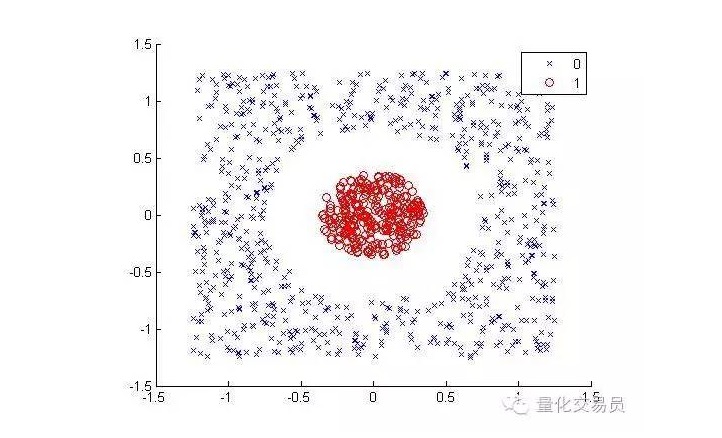
मानव के लिए, यह वर्गीकृत करने के लिए बहुत आसान है (एक गोलाकार रेखा के साथ) । लेकिन मशीनों के लिए एक ही नहीं है। यह स्पष्ट है कि यह एक सीधी रेखा नहीं है (एक सीधी रेखा लाल बिंदुओं को अलग नहीं कर सकती है) । यहाँ हम कर सकते हैं की कोशिश कर सकते हैं कील तंत्र की तकनीक (कील चाल) ।

इन-कोर तकनीक एक बहुत ही चतुर गणितीय तकनीक है जो हमें उच्च-आयामी अंतरिक्ष में रैखिक वर्गीकरण समस्याओं को हल करने में सक्षम बनाती है। अब हम देखेंगे कि यह कैसे किया जाता है।

हम दो-आयामी विशेषण स्थान को तीन-आयामी में बदल देंगे, और जब हम वर्गीकरण कर लेंगे तो हम दो-आयामी में वापस आ जाएंगे।

नीचे दिए गए चित्रों को क्रमशः बढ़ाया गया है और वर्गीकृत किया गया है:

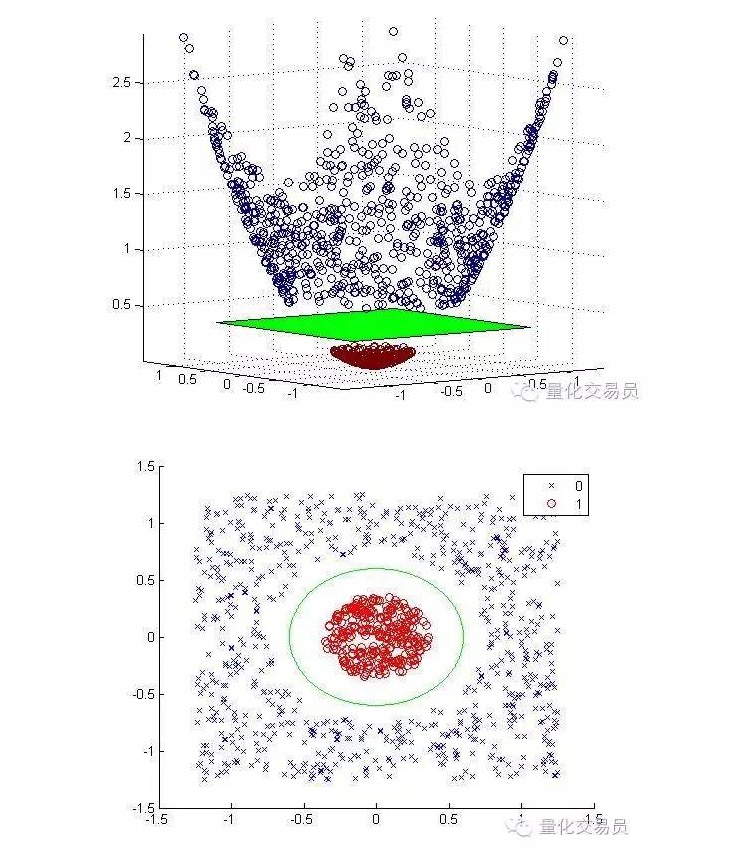
आम तौर पर, यदि आपके पास d इनपुट है, तो आप d आयामी इनपुट स्पेस से p आयामी फीचर स्पेस तक एक मैप का उपयोग कर सकते हैं। ऊपर दिए गए न्यूनतमकरण एल्गोरिदम के समाधान को चलाएं, और फिर अपने मूल इनपुट स्पेस को p आयामी सुपरफ्लैट पर वापस मैप करें।

उपरोक्त गणितीय समाधान की एक महत्वपूर्ण शर्त यह है कि गुणों के स्थान में अच्छे बिंदु नमूना सेट कैसे उत्पन्न किए जाते हैं।

आपको केवल इन बिंदुओं के नमूना सेट की आवश्यकता होती है सीमा अनुकूलन करने के लिए, मानचित्रण को स्पष्ट करने की आवश्यकता नहीं है, और इनपुट स्पेस को सुरक्षित रूप से गणना की जा सकती है क्योंकि उच्च आयामी विशेषता स्पेस में बिंदुओं को कोर फ़ंक्शन ((और कुछ हद तक मर्सर प्रमेय की मदद से)) के माध्यम से गणना की जा सकती है।

उदाहरण के लिए, आप अपने वर्गीकरण समस्या को एक विशाल विशेषता अंतरिक्ष में हल करना चाहते हैं, मान लें कि यह 100,000 आयाम है। क्या आप कल्पना कर सकते हैं कि आपको क्या गणना करने की आवश्यकता होगी? मुझे बहुत संदेह है कि आप इसे पूरा कर पाएंगे। ठीक है, कोरल अब आपको इन बिंदुओं के नमूने की गणना करने देता है, इसलिए यह किनारा आपके कम एकाग्रता वाले आरामदायक इनपुट स्पेस से आता है।

• चुनौती और गोरिल्ला

अब हम जेफ की भविष्यवाणी को हराने की चुनौती के लिए तैयार हैं।

जेफ एक मुद्रा बाजार विशेषज्ञ है और वह 50% पूर्वानुमान सटीकता के लिए रैंडम दांव लगाता है, जो अगले ट्रेडिंग दिन के रिटर्न की भविष्यवाणी करने के लिए एक संकेत है।

हम अलग-अलग बुनियादी समय अनुक्रमों का उपयोग करेंगे, जिसमें वास्तविक मूल्य समय अनुक्रम शामिल हैं, प्रत्येक समय अनुक्रम में 10lags तक की कमाई, कुल 55 विशेषताएं।

हम एक एसवीएम वेक्टर बनाने जा रहे हैं जो 3 डिग्री के कोर का उपयोग करता है। आप सोच सकते हैं कि एक उपयुक्त कोर चुनना एक और बहुत कठिन कार्य है। C और Γ पैरामीटर को कैलिब्रेट करने के लिए, 3 गुना क्रॉस-वैलिडेशन संभव पैरामीटर संयोजन के ग्रिड पर चलता है, और सबसे अच्छा सेट चुना जाएगा।

परिणाम बहुत उत्साहजनक नहीं हैं:

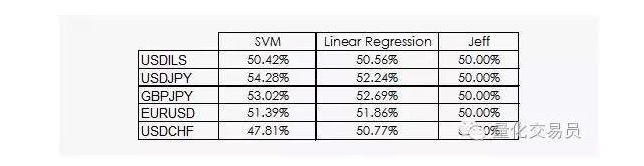
हम देख सकते हैं कि या तो रैखिक प्रतिगमन या एसवीएम वेक्टर जेफ को हरा सकते हैं। हालांकि परिणाम आशावादी नहीं हैं, हम डेटा से कुछ जानकारी प्राप्त कर सकते हैं, जो अच्छी खबर है, क्योंकि डेटा विषयों में, वित्तीय समय अनुक्रम दैनिक लाभ सबसे उपयोगी नहीं है

क्रॉस-सत्यापन के बाद, डेटासेट को प्रशिक्षित और परीक्षण किया जाएगा, हम प्रशिक्षित एसवीएम की पूर्वानुमान क्षमता को रिकॉर्ड करते हैं, और एक स्थिर प्रदर्शन के लिए, हम प्रत्येक मुद्रा के लिए 1000 बार यादृच्छिक विभाजन दोहराएंगे।

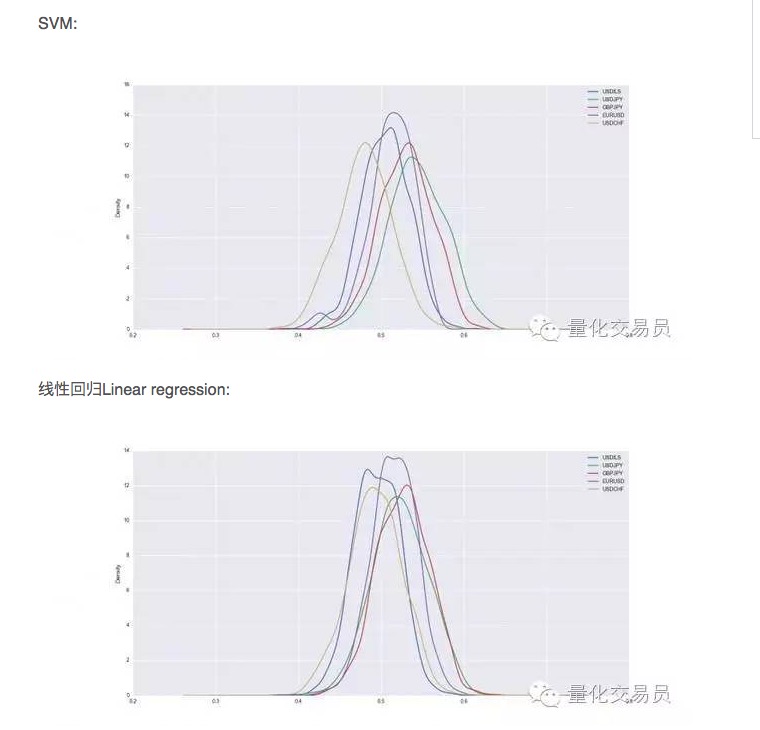
इस प्रकार, कुछ स्थितियों में, एसवीएम सरल रैखिक प्रतिगमन से बेहतर है, लेकिन प्रदर्शन में अंतर थोड़ा अधिक है। उदाहरण के लिए, डॉलर बनाम येन के लिए, हमारे औसत अनुमानित संकेत कुल आवृत्तियों का 54% हैं। यह एक काफी अच्छा परिणाम है, लेकिन चलो इसे और अधिक बारीकी से देखें!

टेड जेफ का चचेरा भाई है, और वह निश्चित रूप से एक गोरापिड है, लेकिन वह जेफ से अधिक बुद्धिमान है। टेड को प्रशिक्षण के नमूने पर ध्यान देना चाहिए, न कि बेतरतीब सट्टेबाजी पर। वह हमेशा प्रशिक्षण सेट के सबसे आम आउटपुट से संकेत देता है। चलो अब स्मार्ट टेड को एक बेंचमार्क के रूप में लेते हैंः

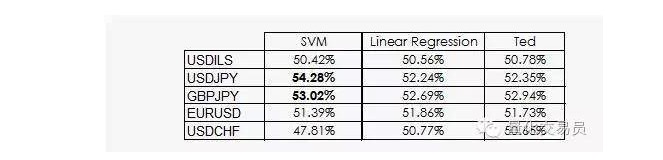
जैसा कि हम देख सकते हैं, अधिकांश एसवीएम का प्रदर्शन केवल इस तथ्य से संबंधित है कि मशीन सीखने के लिए वर्गीकरण की संभावना नहीं है कि यह पूर्वगामी के बराबर हो। वास्तव में, रैखिक प्रतिगमन विशेषता अंतरिक्ष से कोई जानकारी प्राप्त नहीं कर सकता है, लेकिन इंटरसेप्ट () रिटर्न में सार्थक है, और यह तथ्य कि इंटरसेप्ट और किसी विशेष वर्गीकरण को बेहतर प्रदर्शन करने के लिए बेहतर है।

थोड़ी अच्छी खबर यह है कि एसवीएम वेक्टर डेटा से कुछ अतिरिक्त गैर-रैखिक जानकारी प्राप्त करने में सक्षम है, जो हमें 2% की भविष्यवाणी की सटीकता का सुझाव दे सकता है।

दुर्भाग्य से, हम अभी तक यह नहीं जानते हैं कि यह किस तरह की जानकारी हो सकती है, जैसे कि एसवीएम वेक्टर मशीनों के अपने प्रमुख नुकसान हैं, जिन्हें हम स्पष्ट रूप से स्पष्ट नहीं कर सकते हैं।

लेखक: पी. लोपेज़, quantdare में प्रकाशित
WeChat के पब्लिक नंबर से पुनर्प्रकाशित