केली फॉर्मूला - स्थिति नियंत्रण के लिए एक शक्तिशाली उपकरण

** परिकल्पना 1: आपके जीतने की संभावना 60% है और हारने की संभावना 40% है। जीतने पर शुद्ध लाभ दर 100% है और हारने पर भी 100% है। यानी, यदि आप जीतते हैं, तो आप हर 1 डॉलर जीत सकते हैं, और यदि आप हार जाते हैं, तो आप हर 1 डॉलर खो देंगे।

• 1. इस स्टैंडबाय के लिए, हर दांव पर अपेक्षित रिटर्न दांव की राशि का 60% है*1-40%*1 = 20%, उम्मीद है कि लाभ सकारात्मक होगा। यानी, यह एक बाधा है जिसमें हाकिमों का लाभ है, और लाभ बहुत बड़ा है।

तो हम कैसे दांव लगा सकते हैं?

यदि हम गंभीरता से विचार नहीं करते हैं, तो हम सोच सकते हैं कि चूंकि मैं हर बार 20% की उम्मीद कर रहा हूं, तो अधिकतम दीर्घकालिक लाभ प्राप्त करने के लिए, मुझे हर बार जुआ में पूंजी का अधिक से अधिक अनुपात लगाना चाहिए। इस अनुपात का अधिकतम मूल्य 100% है।

लेकिन स्पष्ट रूप से हर बार 100% पूंजी लगाकर जुआ खेलना अनुचित है, क्योंकि एक बार जब कोई जुआ खेल हार जाता है, तो सभी पूंजी पूरी तरह से खो जाती है, और अगले खेल में भाग नहीं ले सकता है, बस चुपचाप खेल छोड़ सकता है। और लंबे समय में, एक बार हारने के बाद यह घटना निश्चित रूप से होगी, इसलिए लंबे समय में यह निश्चित रूप से दिवालिया हो जाएगा।

तो यह निष्कर्ष निकाला गया है कि जब तक एक स्थिरता है, एक बार में पूरी पूंजी खोने की संभावना, भले ही यह बहुत छोटी हो, पूरी तरह से भरा नहीं हो सकता है। क्योंकि लंबे समय में, छोटी संभावना की घटनाएं निश्चित रूप से होती हैं, और वास्तविक जीवन में, छोटी संभावना की घटनाओं की वास्तविक संभावना इसकी सैद्धांतिक संभावना से कहीं अधिक है। यह वित्तशास्त्र में तिल प्रभाव है।

• 2। वापस जा रहे हैं 1 यदि हर बार 100% दांव लगाना अनुचित है, तो 99% का क्या होगा? यदि हर बार 99% दांव लगाया जाए, तो न केवल यह गारंटी दी जाती है कि आप कभी भी दिवालिया नहीं होंगे, बल्कि अगर आप भाग्यशाली हैं, तो आप बहुत अधिक लाभ कमा सकते हैं।

क्या यह वास्तव में है?

हम इस समस्या का विश्लेषण सिद्धांत से नहीं करते हैं, हम एक प्रयोग कर सकते हैं. हम इस गतिरोध का अनुकरण करते हैं, और हर बार 99% का दांव लगाते हैं, देखें कि क्या होता है.

यह सिमुलेशन बहुत ही सरल है और इसे एक्सेल में किया जा सकता है। नीचे दी गई तस्वीर देखेंः

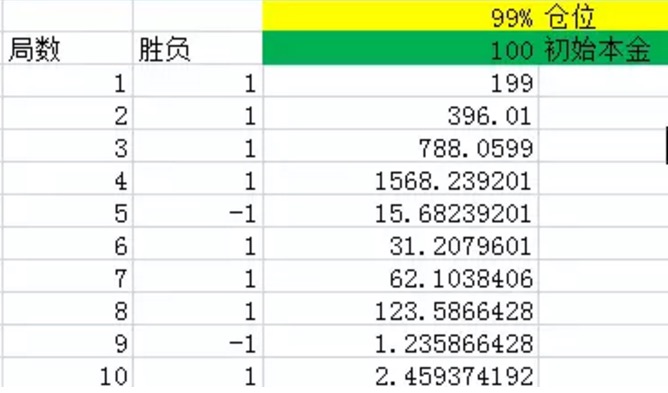चित्र 1

जैसा कि ऊपर दिखाया गया है, पहला कॉलम इकाइयों की संख्या को दर्शाता है। दूसरा कॉलम जीत के लिए है, Excel 60% की संभावना के अनुसार 1 उत्पन्न करता है, यानी 60% की संभावना शुद्ध रिटर्न 1,40% की संभावना उत्पन्न -1 है, यानी 40% की संभावना शुद्ध रिटर्न -1 है। तीसरा कॉलम हर इकाइयों के अंत में सभी धन को रोकता है। इस प्रयोग में, प्रत्येक दांवित स्थिति 99% है, और प्रारंभिक पूंजी 100 है, जो पीले और हरे रंग में क्रमशः चिह्नित है।

जैसा कि आप चित्र से देख सकते हैं, 10 राउंड के बाद, 10 राउंड जीतने की संभावना 8 है, 60% से अधिक है, केवल दो बार खो दिया गया है। लेकिन फिर भी, अंतिम धन केवल 2.46 युआन बचा है, जो मूल रूप से एक घाटा है।

और जब मैं प्रयोगों की संख्या को बढ़ाता हूँ, 1,000 बार, 2,000 बार, 3,000 बार… और जैसा कि आप देख सकते हैं, अंत में, हमारे पास धनराशि लगभग शून्य हो जाती है।

और अगर 99% काम नहीं करता है, तो हम कुछ अन्य अनुपातों के साथ कोशिश करते हैं, जैसा कि चित्र में दिखाया गया है: जैसा कि चित्र से देखा जा सकता है, जब स्थिति को धीरे-धीरे कम किया जाता है, तो 99%, 90%, 80%, 70%, 60% से, समान 10 राउंड का परिणाम बिल्कुल अलग होता है। जैसा कि चित्र से देखा जा सकता है, स्थिति धीरे-धीरे छोटी होने के साथ, 10 राउंड के बाद धन धीरे-धीरे बड़ा होता है।

यदि आप इसे देखते हैं, तो आप धीरे-धीरे देखेंगे कि यह समस्या इतनी सरल नहीं है। यहां तक कि अगर यह इतना बड़ा जुआ है, तो यह भी नहीं है कि आप हर बार पैसा जीत सकते हैं।

तो, हम दीर्घकालिक लाभ के लिए कैसे दांव लगा सकते हैं?

क्या जैसा कि ऊपर दिखाया गया है, अनुपात जितना छोटा होगा उतना ही बेहतर होगा? नहीं, क्योंकि जब अनुपात शून्य हो जाता है तो स्पष्ट रूप से कोई पैसा नहीं कमाया जा सकता।

तो यह सबसे अच्छा अनुपात क्या है?

यह प्रसिद्ध कैली फार्मूला की समस्या है!

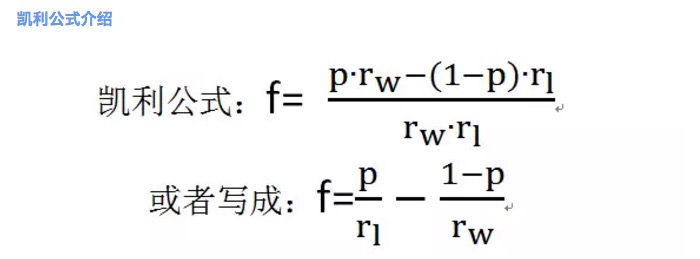चित्र 2

जहां f इष्टतम दांव अनुपात है ∙ p जीत की संभावना है ∙ rw जीत पर शुद्ध लाभ दर है, उदाहरण के लिए, रिंग 1 में rw = 1 ∙ rl हारने पर शुद्ध हानि दर है, उदाहरण के लिए, रिंग 1 में rl = 1 ∙ ध्यान दें कि rl> 0 ∙

कैली के सूत्र के अनुसार, यह गणना की जा सकती है कि समतुल्य 1 में सबसे अधिक दांव का अनुपात 20% है।

हम इस निष्कर्ष को समझने के लिए कुछ प्रयोग कर सकते हैं।

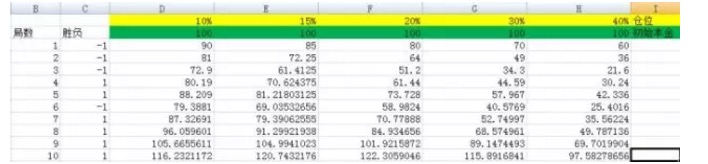चित्र 3

जैसा कि चित्र में दिखाया गया है, हम क्रमशः 10%, 15%, 20%, 30%, 40% की स्थिति सेट करते हैं। उनके संबंधित कॉलम क्रमशः डी, ई, एफ, जी, एच हैं।

और जब मैंने इसे 3000 बार किया, और जब मैंने इसे 5000 बार किया, आप देख सकते हैं कि F स्तंभ का परिणाम सबसे बड़ा है, और अन्य स्तंभों की तुलना में दबाव जड़ संख्यात्मक नहीं है। और F स्तंभ का अनुपात 20% है।

आप केली सूत्र की शक्ति को देख सकते हैं. उपरोक्त प्रयोग में, यदि आप 40 प्रतिशत के अनुपात को चुनने के लिए दुर्भाग्यपूर्ण हैं, तो यह है कि एच कॉलम, तो 5000 के खेल के बाद, आपका मूलधन हालांकि 100 से 22799985.75 हो गया है, यह बहुत बड़ा लाभ है. लेकिन 20% के अनुपात के परिणाम की तुलना में, यह वास्तव में कोई पैसा नहीं जीतने जैसा है.

यह ज्ञान की शक्ति है!

• 3. कैली सूत्र को समझना

कैली सूत्र के गणितीय निष्कर्ष और इसकी जटिलता के लिए, बहुत उच्च और गहन गणितीय ज्ञान की आवश्यकता होती है, इसलिए यहां चर्चा करने का कोई मतलब नहीं है। यहां मैं कुछ प्रयोगों के माध्यम से कैली सूत्र की व्यक्तिपरक समझ को गहरा करूंगा।

हम एक बार फिर से एक दांव पर विचार करेंगे। दांव 2: आपके हारने और जीतने की संभावना 50% है, जैसे सिक्का फेंकना। जीतने पर शुद्ध लाभ दर 1 है, यानी rw = 1, और हारने पर शुद्ध हानि दर 0.5 है, यानी rl = 0.5। यानी जब आप हर एक डॉलर जीतते हैं, तो आप एक और डॉलर जीत सकते हैं, और जब आप हारते हैं तो आप केवल 5 मोना का भुगतान करते हैं।

यह देखना आसान है कि स्टैंडअलोन 2 में 0.25 का अपेक्षित लाभ है, एक और स्टैंडअलोन जिसमें एक बड़ा फायदा है।

कैली के सूत्र के अनुसार, हम प्रत्येक खेल के लिए सबसे अच्छा दांव अनुपात प्राप्त कर सकते हैंः

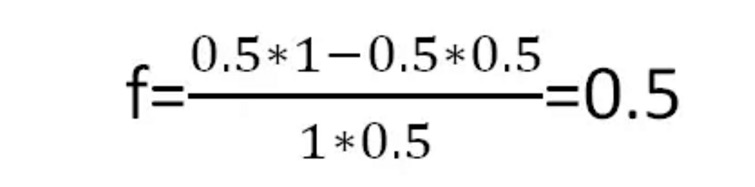चित्र 4

इसका मतलब है कि हर बार जब आप अपना आधा पैसा दांव पर लगाते हैं, तो आपको लंबे समय में सबसे अधिक लाभ मिलता है।

अब मैं प्रयोग के आधार पर औसत वृद्धि दर r की अवधारणा का पता लगाऊंगा

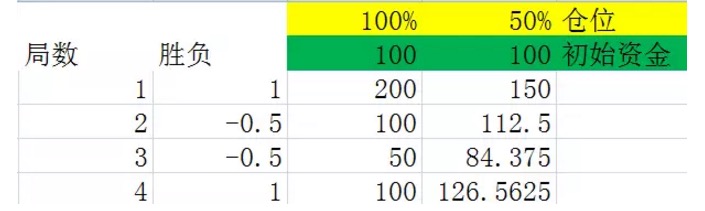
पहले प्रयोग 2.1 को देखें, ये दो आरेखः

चित्र 5

ये दोनों आकृतियाँ स्टैंडआउट 2 के प्रयोग हैं, जिसमें दूसरे कॉलम में जीतने की 50% संभावना है, जो कि 1 है, जो कि 100% लाभ है। 50% की संभावना -0.5 है, जो कि 50% हानि है। तीसरे और चौथे कॉलम में स्टैंडआउट के बाद उनके पास धन है, जो कि क्रमशः 100% और 50% है।

दो चार्टों की सावधानीपूर्वक तुलना करने से निष्कर्ष निकाला जा सकता है कि एक ही संख्या में इकाइयों के बाद, अंतिम परिणाम केवल इन इकाइयों में जीतने वाले इकाइयों की संख्या और हारने वाले इकाइयों की संख्या से संबंधित है, और इन इकाइयों में जीतने वाले इकाइयों और हारने वाले इकाइयों के क्रम से कोई संबंध नहीं है। उदाहरण के लिए, पिछले दो चार्टों में भी 4 इकाइयां की गई हैं, इसी तरह प्रत्येक चार्ट में दो जीतने वाले इकाइयों को खो दिया गया है, लेकिन पहले आरेख का हारने का क्रम जीतने और हारने का क्रम है, और दूसरे आरेख का हारने का क्रम हारने और जीतने का क्रम है। उनका अंतिम परिणाम समान है।

बेशक, यह निष्कर्ष बहुत आसानी से साबित किया जा सकता है (गुणन विनिमय नियम, प्राथमिक विद्यालय के छात्र कर सकते हैं), लेकिन यह साबित नहीं करता है, ऊपर दिए गए दो उदाहरणों को आप अच्छी तरह से समझ सकते हैं।

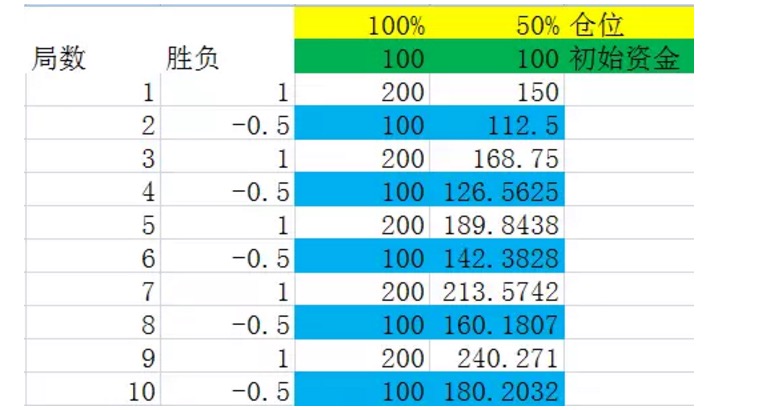
तो चूंकि अंतिम परिणाम जीत-हार के क्रम से संबंधित नहीं है, तो हम मानते हैं कि स्टैंडबाय 2 प्रयोग 2.2 के रूप में किया जाता है, जैसा कि चित्र में दिखाया गया है:

चित्र 6

हम मानते हैं कि जीत और हार के बीच का अंतराल वैकल्पिक है, क्योंकि निष्कर्ष एक यह है कि लंबे समय में परिणामों पर इसका कोई प्रभाव नहीं पड़ता है।

चित्र को देखने से पहले हम एक परिभाषा बनाते हैं। मान लीजिए कि हम किसी न किसी नारे को एक पूरे के रूप में मानते हैं, जिसमें विभिन्न परिणामों की आवृत्ति इसकी संभावना के बराबर है, और इस पूरे का नारे की संख्या सभी शर्तों को पूरा करने वाले कुल के बीच में सबसे कम है, तो हम कहते हैं कि यह एक नारे का सेट है। उदाहरण के लिए, ऊपर दिए गए प्रयोग में, नारे का एक समूह दो नारे का प्रतिनिधित्व करता है, जिसमें से एक जीत और एक हार है।

ऊपर दिए गए आरेख में नीले रंग के अंक को ध्यान से देखें, वे एक स्थिरता के अंत में हैं। आप देखेंगे कि ये संख्याएं स्थिर वृद्धि को बनाए रखती हैं। जब स्थिति 100% है, तो नीले रंग के अंक की वृद्धि दर 0% है, यानी एक स्थिरता के बाद पूंजी की वृद्धि दर 0% है। यह यह भी बताता है कि जब हर बार स्थिति पूरी होती है, तो लॉटरी 2 में लंबे समय तक पैसा नहीं मिल सकता है। जब स्थिति 50% है (यानी कैली सूत्र से प्राप्त होने वाला सबसे अच्छा अनुपात), तो नीले रंग के अंक की वृद्धि दर 12.5% है, अर्थात एक स्थिरता के बाद पूंजी की वृद्धि दर 12.5% है।

यह एक सामान्य नियम है कि प्रत्येक स्टैंडअलोन के बाद वृद्धि दर स्थिति से संबंधित है। और प्रत्येक स्टैंडअलोन के बाद वृद्धि दर जितनी अधिक होगी, उतनी ही लंबी अवधि में अंतिम लाभ होगा।

प्रत्येक समूह की वृद्धि दर के आधार पर प्रत्येक स्थिरता की औसत वृद्धि दर की गणना की जा सकती है g. ऊपर दिए गए चित्र में, प्रत्येक समूह में दो स्थिरता शामिल हैं, तो प्रत्येक स्थिरता की औसत वृद्धि दर

चित्र 7

दीर्घकालिक दृष्टि से, पूंजी को अधिकतम वृद्धि प्राप्त करने के लिए, वास्तव में, केवल r को अधिकतम करना है, अर्थात g को अधिकतम करना है। और सबसे अच्छा दांव अनुपात f वास्तव में max ((g) के समाधान के माध्यम से निकला है।

• 4. कैली फार्मूला के अन्य निष्कर्ष

केली की किंवदंती

कैली सूत्र मूल रूप से एटी एंड टी बेल प्रयोगशालाओं के भौतिक विज्ञानी जॉन लैरी कैली के लिए बनाया गया था, जो अपने सहकर्मी क्लाउड इलवुड शेनोन द्वारा लंबी दूरी की टेलीफोन लाइनों पर किए गए शोध के आधार पर था। कैली ने शेनोन के सूचना सिद्धांत को कैसे लागू करने की समस्या को हल किया है, जो एक जुआरी के पास है, जिसके पास इनलाइन जानकारी है। जुआरी सबसे अच्छा दांव लगाने की राशि तय करना चाहता है, और उसके इनलाइन जानकारी को सही नहीं होना चाहिए (अर्थात, कोई इनलाइन जानकारी नहीं है), जो उसे एक उपयोगी लाभ देता है। सॉप ने अपने काम के समय का उपयोग किया, और कई महीनों के कठिन गणना के माध्यम से, एक गणितीय पत्र लिखा, जिसका शीर्षक था 21 वें स्थान पर जुआ खेलने के लिए पसंदीदा रणनीति। उन्होंने अपने ज्ञान का उपयोग किया, और रातोंरात नेवादा रेनो शहर के सभी कैसीनो पर हमला किया, और 21 वें स्थान पर जुआ खेलने की मेज से सफलतापूर्वक दसियों हजार डॉलर जीते। वह वॉल स्ट्रीट क्वांटिटेटिव ट्रेडिंग हेज फंड के पूर्वज भी थे, जिन्होंने 70 के दशक में पहला क्वांटिटेटिव ट्रेडिंग हेज फंड बनाया। 1962 में प्रकाशित उनके स्तंभ ने जुआरी को हराया, जो वित्तशास्त्र की क्लासिक पुस्तकों में से एक बन गया।

परिप्रेक्ष्य का उपयोग करना

कैली फॉर्मूला का उपयोग वास्तविक जीवन में पैसे कमाने के लिए कैसे करें? यह एक ऐसी स्थिति पैदा करने के लिए है जो कैली के नियम के लिए उपयुक्त हो। मेरे लिए, यह वित्तीय बाजारों से होना चाहिए। मैं हाल ही में ट्रेडिंग सिस्टम के बारे में शोध कर रहा हूं, एक अच्छे ट्रेडिंग सिस्टम के लिए सबसे महत्वपूर्ण क्या है? एक सकारात्मक रिटर्न की उम्मीद के लिए एक नियम खरीद और बेचने का महत्व 10 प्रतिशत है, जबकि एक अच्छा धन नियंत्रण विधि का महत्व 40 प्रतिशत है, और बाकी 50 प्रतिशत लोगों के मानसिक नियंत्रण को नियंत्रित करने के लिए है। और कैली का सूत्र एक ऐसा उपकरण है जो मुझे मेरी पूंजी की स्थिति को नियंत्रित करने में मदद करता है। उदाहरण के लिए, एक स्टॉक ट्रेडिंग प्रणाली है कि मैं पहले से ही अध्ययन किया है, जो एक सप्ताह में एक व्यापार है, एक सप्ताह में एक व्यापार की सफलता की संभावना 0.8 है, विफलता की संभावना 0.2 है. जब सफल 3% कमाने के लिए ((कमिसन, छाप कर कटौती), हर विफलता पर 5% का नुकसान. मैं अंधापन से भरा हुआ था जब मैं कैली सूत्र पता नहीं था, और मैं नहीं जानता था कि मेरी स्थिति सेट गलत है, मनोवैज्ञानिक भ्रामक है. कैली सूत्र का उपयोग करने के बाद, सबसे अच्छा स्थिति 9.33 होना चाहिए, यह है कि अगर उधार ब्याज दर 0 है सबसे तेजी से पूंजी वृद्धि दर प्राप्त करना चाहते हैं, तो लीवरेज ट्रेडिंग का उपयोग करना चाहिए, सूत्र की गणना के माध्यम से प्रति व्यापार औसत वृद्धि दर r के बारे में 7.44% के बराबर है, जबकि पूर्ण व्यापार के लिए औसत पूंजी वृद्धि दर r के बारे में 1.35 है ((यानी वास्तविक आय की उम्मीद है) ।) के बाद भी, यह पता चला है कि यह वास्तव में लीवरेज ट्रेडिंग की तुलना में लीवरेज ट्रेडिंग की गति को बेहतर बनाता है। इसने मुझे समझाने के लिए लीवरेज फंड का उपयोग करने बेशक, कैली सूत्र वास्तविक उपयोग में इतना सरल नहीं हो सकता है, और कई कठिनाइयों को दूर करने की आवश्यकता है। जैसे कि लीवरेज्ड एक्सचेंजों की आवश्यकता के लिए पूंजी की लागत, जैसे कि वास्तविकता में धन असीमित रूप से विभाजित नहीं है, जैसे कि वित्तीय बाजार में यह उतना सरल नहीं है जितना कि ऊपर उल्लिखित सरल ठहराव। लेकिन फिर भी, कैली के सूत्र ने हमें आगे बढ़ने का रास्ता दिखाया है।