गणित और जुआ

• हम जानते हैं कि जुआ संभावनाओं का खेल है, और यह कुछ अजीब जुआ परिणामों है कि गणितज्ञ पास्कल और महान गणितज्ञ Fermat, जो पत्रों के माध्यम से, कुछ संभावना सिद्धांतों की पेशकश की है, जो संभावना सिद्धांत की स्थापना की रुचि पैदा कर दी है. आज के गणित में कुछ जुआ में संभावना के बारे में दिलचस्प विषयों का परिचय है, तो आप जानते हैं कि, जुआ खेलने के लिए, बारीकी से विचार करना होगा.

• 1. सही जुआ

एनबीए टीम, लेकर्स और बैल के बीच एक खेल है, और दोनों टीमों के वफादार प्रशंसक हैं, तो उन्हें बैल और बैल कहते हैं। प्रशंसकों को निश्चित रूप से लगता है कि वे जिस टीम का समर्थन करते हैं वह जीतने की अधिक संभावना है, इसलिए वे आपके साथ दांव लगाना चाहते हैं। मान लीजिए कि बैल को लगता है कि बैल जीतने की संभावना p है, और बैल को लगता है कि बैल जीतने की संभावना q, p और q दोनों 50% से अधिक होनी चाहिए। अगला हिस्सा मजेदार है, हम हमेशा आसानी से एक तरीका डिजाइन कर सकते हैं, बैल और बैल के साथ खेलते हैं, लेकिन परिणाम चाहे जो भी हो, हम हमेशा जीत सकते हैं!

यह इस तरह है: हम एक ही खेल खेलते हैं, जैसे कि कंगन और एक ही तरह का बैल खेलते हैं, अगर हम जीतते हैं तो हम y प्राप्त करते हैं, और अगर हम हारते हैं तो हम x खो देते हैं, जब तक कि y>x हम जीत जाते हैं। और x और y को केवल निम्नलिखित दो सरल असमानताओं को पूरा करने की आवश्यकता है, कंगन और बैल के लिए अपेक्षित लाभ सकारात्मक है, और हमारे साथ दांव लगाते हैंः

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

y>x की सीमा के साथ, चित्रित किया गया क्षेत्र तीन सीधी रेखाओं से घिरा हुआ है, जो किसी भी बिंदु के लिए निर्देशांक मूल्य ((x, y) है। यदि p>q है, तो समाधान निम्न चित्र में नीले रंग का हिस्सा हैः

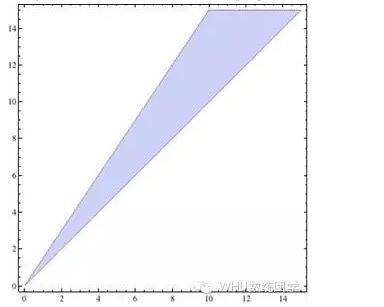
यह सवाल पूरी तरह से हल हो गया है, लेकिन एक और संदेह है, और मुझे लगता है कि पाठक जल्द ही इस बात की बेतुकी बात को समझेंगेः चाहे वे यांग या बैंग का परिवार हो, वे सकारात्मक आय की उम्मीद करते हैं, अर्थात, वे लंबे समय तक पैसा कमाते हैं, और हम लगातार लाभ कमाते हैं, तो यह पैसा कहां से आता है, और हर कोई इसे कैसे कमा सकता है?

• ### दो-तीन कार्ड का धोखा

यह एक और चतुर पहेली है, हम पहले तीन कार्ड तैयार करते हैं, कार्ड नंबर 1 का उल्टा काला है, कार्ड नंबर 2 का उल्टा लाल है, कार्ड नंबर 3 का एक तरफ काला है, और एक तरफ लाल है। फिर कार्डों को एक बॉक्स में रखो, उन्हें हिलाओ, और अपने प्रतिद्वंद्वी को एक समतल पत्ती खींचने के लिए दें। फिर उसे और उसके पहेली के विपरीत रंग और सकारात्मक के समान। यह पहेली निष्पक्ष लगती है, जैसे कि एक सतह पर एक काला पत्ती है, तो कार्ड नंबर 1 या 3 नहीं है, विपरीत रंग काला या लाल नहीं है, और सभी संभावनाएं ¹⁄₂ हैं।

वास्तव में, हमारे जीतने की संभावना ¹⁄₂ नहीं है, बल्कि ²⁄₃ है, और इस पहेली में सबसे ज्यादा उलझन में डालने वाली बात यह है कि हमारे पास दो-तरफ़ा पहेली है। हम तीन कार्ड नहीं, बल्कि छह कार्ड खींचते हैं: तीन काले और तीन लाल। हम उन छह को A, B, C, D, E और F कहते हैं:

जब एक खिलाड़ी काले रंग की ओर जाता है, तो A, C और D तीन संभावित स्थितियां हैं, और उनके पीछे क्रमशः D, F और A हैं, जिसमें काले रंग की स्थिति ²⁄₃ होती है।

इस समस्या को सबसे पहले 1889 में फ्रांसीसी गणितज्ञ जोसेफ लुई फ्रेंकोइस बर्ट्रैंड द्वारा प्रस्तुत किया गया था, क्योंकि इस समस्या का परिणाम अप्रत्याशित था, इसे बर्ट्रैंड के बॉक्स विरोधाभास के रूप में जाना जाता है। 1950 में अमेरिकी गणितज्ञ वॉरेन वेवर ने ऊपर दिए गए कार्ड खेलने की शुरुआत की, जिसे मार्टिन गार्डनर ने तीन-कार्ड धोखे के रूप में जाना था।

• ### 3. अनोखी मैंगनीज

कभी-कभी हम जुआ खेलना शुरू करते हैं और पानी छोड़ देते हैं, पहले दूसरों को कुछ पैसे कमाते हैं, लंबी लकीर खींचते हैं, और अंत में एक बड़ा जाल खत्म हो जाता है। नीचे एक उत्कृष्ट उदाहरण है। चार लोग ब्रिज खेल रहे हैं, मैं पहले कहता हूंः आओ एक पहेली खेलते हैं, मेरे पास अब एक ए है, आप अनुमान लगा सकते हैं कि मेरे पास और ए हैं? इस मामले में आप शायद हार जाएंगे, और इस समय आप चुपचाप एक रंगीन ए का चयन करेंगे, जैसे कि ब्लैक ए, और जब एक निश्चित दौर में ब्लैक ए पकड़ा जाता है, तो यह मौका आता हैः चलो एक और पहेली खेलते हैं, अब मेरे पास ब्लैक ए है, आप अनुमान लगा सकते हैं कि मेरे पास और ए नहीं है?

बहुत से लोगों को लगता होगा कि दो लहसुन के बीच कोई अंतर नहीं है, और एक आड़ू के साथ कोई फर्क नहीं पड़ता। लेकिन उनके बीच का अंतर अविश्वसनीय रूप से बड़ा है। आइए पहले लहसुन के लिए संभावना की गणना करेंः

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

इस बार मैं खुद को और A, खोने के लिए आसान है. लेकिन पहली बार के बाद से, सभी के दांव लगाने की इच्छा को गति दी गई है, एक बार जब मैं दूसरी बार नहीं बदलना चाहता था, तो मैंने दांव लगाया, और फिर मैंने कहा कि मेरे पास और A नहीं है, ठीक है, हम नीचे हैं. नीचे हम पाएंगे कि दूसरी बार की संभावना बहुत अलग है:

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

डब्ल्यूएचयू गणितीय समूह विज्ञान