जुआरी की ट्रेडिंग रणनीति

इस लेख का विषय वास्तव में जॉब्स द्वारा कही गई एक बात है: We’re making it less random to make it feel more random (हम इसे कम यादृच्छिक बना रहे हैं ताकि यह अधिक यादृच्छिक महसूस हो) ।

लंदन ट्रेडर नोटः निम्नलिखित पैराग्राफ अग्रलेख के रूप में हैं, लेखक को सलाह दी जाती है कि पहले अग्रलेख को पढ़ें और फिर मूल पाठ पढ़ें, ताकि आप जो के सहायक के ज्ञान को बेहतर ढंग से जान सकें।

• ##### संयुक्त राज्य अमेरिका की स्वतंत्रता की घोषणा में सबसे अधिक उल्लिखित वाक्यांश यह है कि “सभी पुरुष समान हैं”। लेकिन यह एक तथ्य की घोषणा के बजाय, यह उस इच्छा के करीब है जो हम प्रार्थना के दौरान करते हैंः हम चाहते हैं कि सभी पुरुष समान हों।

इच्छाओं से संकेत मिलता है कि ऐसा कुछ भी नहीं है: कोई बच्चा गाड़ी से कार चलाता है, कोई आईक्यू 180 है, कोई तीन साल की उम्र में पेंसिल से कैलकुलस करता है और पतला सोना लिखता है। इन लोगों से मिलने के बाद, हम केवल एक ही कर सकते हैं जो सोचता है कि कैसे जीवन के बाद के जीवन को बचाने के लिए।

आज हम बात करेंगे उन सभी असमानताओं के बारे में जो उपरोक्त से भी अधिक असमान हैं: क्यों कुछ लोग हमेशा जीतते हैं!

हर कंपनी में ऐसे कई लोग होते हैं, हर साल एक लॉटरी होती है, और वे मंच पर पुरस्कार जीतते हैं, कहते हैं कि भाग्यशाली होने के लिए कोई बात नहीं है। मैंने एक बार कॉफी खरीदी थी, एक बार खरीदी थी, एक बार खरीदी थी, एक बार खरीदी थी, एक बार खरीदी थी, रात को सो नहीं सका (निश्चित रूप से, शायद बहुत अधिक कैफीन) ।

यह एक ऐसा अनुभव है जिसे लगातार जीत कहा जा सकता है।

लगातार पुरस्कार जीतना एक अन्याय है, यह हमेशा किसी और की माँ के साथ होता है

मान लीजिए कि कंपनी में 200 लोग हैं, और वार्षिक लॉटरी में शीर्ष पुरस्कार जीतने की संभावना ¹⁄₂₀₀ = 0.5% है, और लगातार दो वर्षों में शीर्ष पुरस्कार जीतने की संभावना 0.5% × 0.5% = 25 मिलियन में से 25 है, जो काफी कम है।

लेकिन वास्तव में यह किसी विशेष व्यक्ति (आप) की लगातार दो वर्ष तक प्रथम स्थान प्राप्त करने की संभावना है। किसी भी व्यक्ति की लगातार दो वर्ष तक प्रथम स्थान प्राप्त करने की संभावना 200 × 0.5% × 0.5% = 0.5% है, जो आपके ड्रॉ में प्रथम स्थान प्राप्त करने की संभावना के बराबर है।

3 साल में एक व्यक्ति के 2 बार पुरस्कार जीतने की संभावनाः 1 - 3 साल में 3 अलग-अलग विजेताओं की संभावना = 1-200 × 199 × 198 / 200 × 200 × 200) = 1.5%

और अगर आपको लगता है कि आप मुझे तीन साल में एक बार पुरस्कार दे सकते हैं, तो यह भी उचित है कि आप तीन साल में दो बार पुरस्कार जीतें।

मैं आपको पूरे साल धूम्रपान करने के लिए मजबूर कर सकता हूं।

क्या यह अधिक भयावह है कि एक ही वर्ष में एक बार फिर से विजेता बनने वाला व्यक्ति खुद को मई दिवस के लिए स्वर्ण गीत पुरस्कार का विजेता मानता है?

उदाहरण के लिए, 200 लोगों की कंपनी के उदाहरण पर वापस आते हुए, मान लीजिए कि 10 पुरस्कार हैं, और कर्मचारी पुरस्कार जीत सकते हैं। इस प्रकार, किसी भी व्यक्ति के लिए 2 से अधिक पुरस्कारों की संभावना हैः 1- 10 पुरस्कारों के 10 अलग-अलग लोगों द्वारा प्राप्त होने की संभावना) = 1-200 × … × 191 / 200 × … × 200) = 20.4%

एक मौका है कि एक सहकर्मी आपको बताता है कि वह मुझे जीतने के लिए जीतता है … … … … . .

लंदन के व्यापारीः अब बात हो गई है

यादृच्छिक नहीं यादृच्छिक

इस तरह की मूर्खता बहुत संभावना नहीं लगती है, लेकिन वास्तव में जीवन में इस तरह की मूर्खतापूर्ण घटना है, जैसे कि यादृच्छिक रूप से प्लेलिस्ट से गाने चलाना, यदि आपने प्लेलिस्ट से गाने नहीं हटाए हैं, तो 10 गानों की प्लेलिस्ट, एक बार यादृच्छिक क्रम में (यानी एक भी गीत दोहराया नहीं जाता है) 10 गाने सुनने के लिए, केवल 10!/1010 = 0.036%, असंभव कार्य की संभावना से कम है, और टॉम क्रूज़ की तुलना में कम है। सीधे प्लेलिस्ट से हटाए गए गानों को सुनने से समस्या हल हो सकती है, लेकिन दोष यह है कि 1 गीत को 10 बार सुनने से पहले 2 बार सुनने के लिए कम से कम है।

ऐप्पल के यादृच्छिक प्लेबैक प्रोग्राम के बारे में कहा जाता है कि यह विभिन्न गायकों, विभिन्न धुनों को एक दूसरे के साथ खेलता है, जिससे उपयोगकर्ता को लगता है कि प्रत्येक गीत के बीच कोई संबंध नहीं है। जॉब्स ने कहा था, “हम इसे कम यादृच्छिक बना रहे हैं ताकि इसे और अधिक यादृच्छिक महसूस किया जा सके”।

• #### ठीक है, तैयारियां पूरी हो चुकी हैं, अब हम मूल पाठ शुरू कर सकते हैं।

लेनदेन के जुआरी मॉडल के बारे में बात करें (विशिष्ट व्यावहारिक उदाहरण मार्क वॉलबर्ग की नवीनतम फिल्म जुआरी / द जुआरी को देखें, लेकिन लंदन के व्यापारियों ने कहा कि फिल्म वास्तव में अच्छी नहीं लगती है)

व्यापार करते समय, जब भी एक दिशा का अनुमान लगाएं, अगर गलत हो तो रिवर्स डबल करें और फिर से पोजीशन खोलें, कीमत हमेशा वापस आ जाएगी, यह संभव नहीं है कि यह वापस न आए (नहीं गिर सकता है) । मैं हर बार डबल करता हूं, फिर से, एक बार मैं वापस आ गया हूं और पैसा जीता हूं।

एक पैसा खोना ठीक है, अगली बार दो डालर का दांव लगाओ, अगर तुम जीत जाओ तो चार डालर, एक डालर और, अगर तुम फिर से गलत हो जाओ तो चार डालर लगाओ, फिर से आठ डालर, कुल निवेश 1+2+4=7, या एक डालर।

इस तरह से, आपको यह जानने की आवश्यकता नहीं है कि आप हर बार 1 युआन कैसे कमा सकते हैं।

और फिर, और फिर, और फिर, और फिर, और फिर, और फिर, और फिर, और फिर!

लेकिन यह क्लासिक जुआरी का मिथक, जैसा कि पोंटेज़ घोटाले में है, अविश्वसनीय रूप से जीवंत है, लंबे समय तक टिका है, खड़ा है, और सट्टेबाजों की पीढ़ियों को धोखा दे रहा है।

एक सिक्का फेंकने पर सकारात्मकता की संभावना या अपेक्षित मूल्य 0.5 है, लेकिन यदि केवल एक बार फेंक दिया जाता है, तो सकारात्मकता की संभावना 0 या 1 है (दूरस्थ विचलन 0.5) । जैसे-जैसे सिक्का फेंकने की संख्या बढ़ती है (यानी, नमूना बड़ा होता है), सिक्का के सकारात्मक होने की संभावना धीरे-धीरे 0.5 के करीब हो जाती है। लेकिन संज्ञानात्मक मनोविज्ञान के छोटे-छोटे संख्या के नियम के अनुसार, लोग आमतौर पर नमूना आकार के प्रभाव को अनदेखा करते हैं, यह मानते हुए कि छोटे नमूने और बड़े नमूने में समान अपेक्षित मूल्य है।

एक बार जब आपके पास सकारात्मकता है, तो आपको लगता है कि नकारात्मकता की संभावना बढ़ जाती है।

एक बार लाल रंग के कई बार आने के बाद, हमेशा कई लोग काले रंग पर ध्यान केंद्रित करने के लिए चुनते हैं।

इस रणनीति का उपयोग करते हुए, वित्तपोषण की वक्र निश्चित रूप से इस प्रकार होगीः

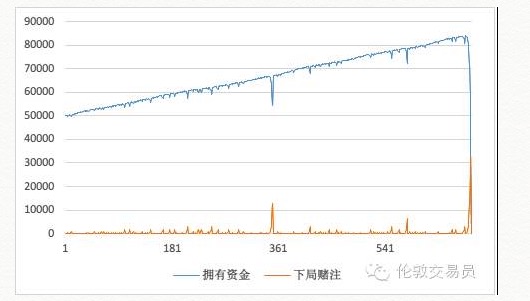
अभ्यास के दौरान, पूंजी वक्र एक तरह से ऊपर की ओर है, और ऐसा लगता है कि यह काफी स्थिर है. अभ्यास के अंत में 361 बार के आसपास, हम एक बार में एक गलती देख सकते हैं, और फिर रणनीति के साथ रहते हैं, न केवल वापसी, लेकिन यह भी एक तरह से ऊपर की ओर बढ़ना जारी है.

बेशक, इस तरह की रणनीतियों का अंतिम परिणाम शून्य होना चाहिए, कोई भी कीमत नहीं है। न केवल कोई कीमत नहीं है, लेकिन यह भी एक मजबूत दर्दनाक भावना है कि एक अच्छा सपना टूट जाएगा।

मैंने ऐसा एक से अधिक बार देखा है। हर बार जब कोई मुझे एक नए व्यापारिक विचार के बारे में बताता है, जो लगभग वापस नहीं लिया जाता है, तो मुझे संदेह होता है कि क्या कोई और जुआरी की गलती में फंस गया है।

जो लोग इसमें फंस जाते हैं, वे अक्सर खुद को नहीं निकाल पाते हैं, तथाकथित ग्रिड ट्रेडिंग रणनीति, मार्टिनगेलर पट्टा विधि, और इसी तरह, कभी भी झूठे झूठे के चंगुल से नहीं बच सकते हैं, लेकिन यह निश्चित रूप से अनंत जीवन शक्ति प्राप्त कर सकता है।

क्योंकि एक रणनीति की लोकप्रियता का निर्धारण कभी भी उसकी कमाई की क्षमता से नहीं होता है, बल्कि यह है कि वह मानवता के अनुरूप है या नहीं।

ऐसा लगता है कि दुनिया में किसी भी चीज को जब तक वह मानवीय अपेक्षाओं को पूरा करती है, तब तक वह मजबूत जीवन शक्ति प्राप्त करती है। यह पंकज घोटाले की तरह है। नेट रणनीति भी अच्छी है, मार्टिंगेल रणनीति भी, शुरुआत में हमेशा आपको एक बहुत ही स्थिर रिटर्न देती है। उम्मीदें। और कोई धन वापसी नहीं।

मानव मस्तिष्क लाभ से अधिक हानि से घृणा करता है। यह एक रणनीति है जो हमारे पूर्वजों ने प्राचीन काल में विकसित की थी, क्योंकि हमारे पूर्वजों के पास बहुत लंबे समय तक सोचने के लिए समय नहीं था, पेट भरने के लिए, और फिर इस भोजन को खत्म करने के लिए।

हालांकि, मानव सभ्यता तेजी से विकसित हो रही है, दिन-ब-दिन बदलती है, जैविक अर्थों में मस्तिष्क अभी भी एक इकाई के रूप में लाखों वर्षों में विकसित हो रहा है। एक प्राचीन मस्तिष्क आज के वित्तीय बाजार का सामना कैसे कर सकता है? इसलिए, बाजार को अपने व्यक्तिपरक भावनाओं के आधार पर न्याय न करें, रणनीति का न्याय न करें; मानव ज्ञान पर भरोसा करने की आवश्यकता है, न कि भावनाओं पर।

(न्यूरोइकॉनॉमिक्स, दूसरा संस्करण)

दोस्तों, अगर आपको एक अच्छी ट्रेडिंग रणनीति की सिफारिश की जाती है, और प्रमोटरों को विश्वास है कि आपको बाजार के बारे में किसी भी अंतर्दृष्टि की आवश्यकता नहीं है, तो आपको अपने धन के प्रबंधन को अपने मुख्य नियम के रूप में रखना चाहिए। सावधान रहें, यह एक और धोखाधड़ी का नया रूप हो सकता है।

वित्तीय बाजार एक तरह से थर्मोडायनामिक्स की तरह हैं, और हमें थर्मोडायनामिक्स के निष्कर्षों को ध्यान में रखना चाहिए ताकि हम धोखाधड़ी से बच सकें।

सबसे महत्वपूर्ण बात यह है कि ऊर्जा संरक्षण का नियम है, ऊर्जा न तो पैदा होती है और न ही गायब होती है। यदि आप बाजार में कोई योगदान या अंतर्दृष्टि नहीं देते हैं, और यदि आप बाजार को अधिक कुशल संसाधन नहीं बनाते हैं, तो आप बिना किसी लाभ के लाभ नहीं कमा सकते हैं, जो कि प्राकृतिक कानूनों का उल्लंघन है।

कोई भी रणनीति प्रकृति के नियमों का उल्लंघन नहीं कर सकती है, यह एक निश्चित बात है। प्रत्येक प्रभावी रणनीति को सूचना असममितता का लाभ उठाना होगा, या सुपरमैन अंतर्दृष्टि का लाभ उठाना होगा, या बाजार को अधिक कुशल बनाने के लिए अपने स्वयं के संसाधनों का उपयोग करना होगा। आपको इसके अनुरूप योगदान देना होगा ताकि बाजार आपको वापस कर सके।

ग्रिड ट्रेडिंग रणनीति (यदि आप गलत हैं, तो आप दोगुने हो जाएंगे) और यह उम्मीद करना कि आप कोई आउटपुट नहीं देंगे, लेकिन आपको लाभ मिलेगा, यह एक पागलपन है, जैसे कि आप एक अनंत प्रेरक बनाना चाहते हैं।

ट्रेडिंग लागत को ध्यान में रखे बिना, ग्रिड रणनीति ((एक दिशा में काम करने के लिए, कभी भी पोजीशन को कम करने के लिए, एक बार सही होने पर, तुरंत मुनाफा कमाएं, एक बार गलत होने पर, रिवर्स करें, स्थिति को दोगुना करें)) की अपेक्षित आय शून्य है।

यह शून्य प्रत्याशित लाभ केवल गणित है, और लेन-देन की लागत को ध्यान में रखते हुए, प्रत्याशित लाभ नकारात्मक है, अर्थात, एक निश्चित नुकसान रणनीति।

एक बार फिर, यह देखते हुए कि ग्रिड रणनीति का कहना है कि अतिरिक्त निवेश की आवश्यकता है, यह लाभप्रदता मॉडल के अनुरूप है, और इसलिए, कई बार गलत होने के बाद, नए निवेश की आवश्यकता खगोलीय संख्या होगी।

वित्तपोषण की क्षमता, अंततः, एक ऊपरी सीमा है, क्योंकि इस प्रतिबंध के अस्तित्व के कारण, एक कम शानदार अंत अपरिहार्य है।

सभी समझदार लोग समझते हैं, दृढ़ रहना, लेकिन इतना मुश्किल है।

लेकिन, लेकिन! इतने दिनों तक आसमान में रोटी नहीं होने के बाद, सब निराश हो गए, हम जानते हैं कि जुआरी गलत हैं, चलो देखते हैं कि चेस में एक ट्रिक के लिए कौन से बुद्धिमान हैं।

एक अन्य यूजर ने ट्वीट कियाः

यह एक साधारण यांत्रिक उपकरण है जिसमें दो सिक्के होते हैं, जो काले और सफेद को दर्शाते हैं। खिलाड़ियों को खेल के सिक्कों को दांव पर लगा दिया जाता है। जब सभी खिलाड़ियों के सिक्के समाप्त हो जाते हैं, तो मशीन शुरू हो जाती है और यादृच्छिक रूप से दो छोटे काले और सफेद छेद से एक गेंद निकलती है। हारने वाला खाली है, विजेता को दोगुना पुरस्कार मिलता है।

इस मॉडल के तहत, खिलाड़ियों को जो भी मिश्रित रणनीतियों का उपयोग करना चाहिए, उन्हें हमेशा शून्य लाभ की उम्मीद करनी चाहिए।

मुझे नहीं पता था कि कैसे जीतना है, और मुझे नहीं लगता कि यह संभव है।

एस जुंग ने आगे कहा कि उनकी रणनीति बहुत सरल है। अर्थात्, एक बार एक रंग चुनें, जैसे कि काला। तो पहली बार एक सिक्का काला में दांव लगाएं; अगर हार गए, तो दूसरी बार दो सिक्के काली पर जारी रखें; अगर फिर से हार गए, तो तीसरी बार चार सिक्के काली … ऐसा ही। यदि n राउंड नहीं जीते, तो n + 1 राउंड में 2 का n चौथाई काला में दांव लगाएं। यदि एक बार जीत हो जाए, तो रिसीवर एक, दो, चार डॉलर का एक नया चक्र शुरू करता है।

इस पद्धति का लाभ यह है कि कोई फर्क नहीं पड़ता कि पहले कितना पैसा खो दिया है, अगर आप अगली बार जीतते हैं, तो आप अपने नुकसान को वापस कर सकते हैं, और एक डॉलर का शुद्ध लाभ उठा सकते हैं, जबकि लगातार असफलता की संभावना बहुत कम है, केवल 1 / 2 ^ n) ।

बेशक, यह तरीका मेरे लिए पर्याप्त नहीं है। जब मैंने पहले कहा था कि किसी भी मिश्रण रणनीति की उम्मीद शून्य है, तो स्वाभाविक रूप से इस रणनीति को शामिल किया गया था।

इस रणनीति में हारने की संभावना बहुत कम लगती है, फिर भी शून्य क्यों? यह बहुत आसान है, क्योंकि उसका दांव बहुत बड़ा है, मान लीजिए कि वह पहले 7 बार हार गया है, तो उसे आठवीं बार 256 डॉलर का जुआ खेलना होगा ताकि वह फिर से जीत सके। लेकिन आठवीं बार फिर से हारने पर, 511 डॉलर का नुकसान हुआ, और मुझे नहीं लगता कि एक प्राथमिक छात्र एस के पास आगे बढ़ने के लिए पूंजी है। दूसरे शब्दों में, असफल होने की संभावना छोटी है, लेकिन हर सात या आठ बार होने वाली छोटी संभावना की घटना में नुकसान घातक है, जिससे उसे कुछ हफ्तों के भीतर खेलना बंद हो जाता है। इसके अलावा, इस रणनीति में से प्रत्येक सफल चक्र में केवल 1 डॉलर का लाभ होता है, स्थिर लाभ प्राप्त करने के लिए इसे बहुत बार दोहराया जाना चाहिए। प्रत्येक चक्र में दो बार गिनती करने के लिए, यह अनुमान लगाया गया है कि 20404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040

सच कहूं तो, मुझे इस रणनीति की व्यवहार्यता पर बहुत संदेह है।

यहाँ हम देख सकते हैं कि यह एक सरल रणनीति है, जैसे कि ग्रिड रणनीति, जो कि जुगाली के मिथक का एक क्लासिक रूप है। यहाँ, मैंने सोचा था कि यह एक और जुगाली था।

हालांकि, वास्तव में, एस-जुन ने इस रणनीति को अपनाया, हर बार गेम रूम में 20-30 सिक्के कमाने के बाद, वह एक दोपहर के लिए अन्य गेम खेलने के लिए चला गया। मैं न केवल पूरी तरह से उसके एक तरफ़ा शब्दों पर विश्वास करता हूं, बल्कि उसके बाद के विश्लेषण ने मुझे विश्वास दिलाया कि यह रणनीति वास्तव में काम करती है, क्योंकि मेरे पहले के विश्लेषण में घातक त्रुटि थी।

और अगर आप इसे पूरी तरह से निष्पक्ष खेल मानते हैं, तो यह आपकी घातक गलती है।

यहाँ एक दिलचस्प जगह है, सुपर सूखा। (लंदन के व्यापारियों ने इसे ध्यान से पढ़ने की सलाह दी है)

इसका क्या मतलब है?

S君 मुस्कुराया और कहा, “आपका विश्लेषण गणितीय रूप से निर्विवाद है। लेकिन यह मत भूलो कि आपका निष्कर्ष यह है कि खिलाड़ी की अपेक्षा शून्य है, दूसरे शब्दों में, जमींदार की अपेक्षा भी शून्य है। लेकिन क्या जमींदार की आय वास्तव में शून्य है, और यदि शून्य है, तो क्या वह इस मशीन को किराए पर लेने के लिए घाटे में नहीं है? “

वास्तव में, श्री एस का विचार मैं भी सोच रहा था कि जुआरी निश्चित रूप से पैसा कमाएगा। एकमात्र तरीका यह है कि जुआरी छोटी गेंद को हेरफेर कर रहा है। एक चरम परिकल्पना कीजिए, अगर कोई व्यक्ति सफेद रंग में दस हजार जुआ खेलता है, तो उसके जीतने की संभावना बहुत कम है, और जुआरी कई हफ्तों तक बहती हुई पूर्वी धारा की ओर नहीं देखेगा। हालांकि कोई भी गेम रूम में दस हजार जुआ नहीं कमाएगा, लेकिन एस के अनुसार, एक बार में 200-300 जुआ खेलने वाले वयस्क देशभक्तों के लिए यह असामान्य नहीं है।

जुआरी के लिए, सबसे लालची स्थिति यह है कि वह हर बार छोटी गेंद को कम दांव वाले रंग पर गिरने के लिए नियंत्रित करता है, जिससे वह हर बार जीतता है। लेकिन यह स्पष्ट रूप से सामान्य नहीं है, और यदि यह बहुत स्पष्ट है और खिलाड़ी को पता है, तो यह सुखद खेल नहीं हो सकता है।

घर के मालिकों को जीत या हार का सामना करना पड़ता है, और आम तौर पर एक उचित छोटे से लाभ को बनाए रखना चाहिए, जैसे कि हर दस में से 10%, हालांकि यह बड़ा नहीं है, लेकिन यह किसी भी वित्तीय संपत्ति की तुलना में बहुत अधिक लाभदायक है।

मुझे कुछ संदेह है, तो क्या यह आपकी रणनीति नहीं है कि खिलाड़ियों को हर बार अल्पसंख्यक पक्ष में खड़ा होना चाहिए?

S ने आगे कहा कि यह मशीन प्रत्येक खिलाड़ी के सिक्के को आगे की ओर फेंकने के लिए सेट की गई है। यदि आप खिलाड़ी के साथ संवाद नहीं करते हैं, तो आप मूल रूप से अन्य खिलाड़ियों को उस स्थान पर सिक्के फेंकने के लिए नहीं देख सकते हैं, और हर बार अन्य खिलाड़ियों के साथ संवाद करना और निर्णय लेना असंभव है।

मैं: तो क्या तुम मानते हो कि तुम थोड़े से लोगों को जीतते हो? क्या तुम मानते हो कि इस गोताखोरी के नियम का कोई व्यावहारिक अर्थ नहीं है?

S: आप इसे अलग-थलग नहीं देख सकते हैं, और जब आप समझते हैं कि यह एक खेल है, तो आप पहले से कहीं अधिक आगे बढ़ चुके हैं।

मैं: अरे, और भी कुछ हैं, मुझे लगता है कि कुछ जीतने से बॉस को पैसा मिल गया है।

S: जुआ मालिक पहले से ही मशीन और साइट की लागत वहन करता है, यानी वह इस खेल में देनदार है। न केवल वह घाटा नहीं कर सकता, बल्कि उसे पैसा भी कमाना होगा। और पैसा कमाना दो आवश्यक शर्तों के साथ है, एक यह है कि किसी को एक बार में भारी राशि नहीं निकालना चाहिए, जिसे कुछ जीत कहा जाता है, लेकिन एक और महत्वपूर्ण शर्त यह है कि जुआ स्थिर आय के आधार पर यथासंभव अधिक खिलाड़ियों को आकर्षित करे।

मैं: अरे, जुआरी के लिए, यह जुआ कर मुक्त है, और जीतने और हारने के लिए हर तरफ दिखता है, यह वास्तव में बहुत आकर्षक है

S: हाँ, लेकिन जो लोग गणित के बारे में नहीं सोचते हैं, वे ऐसा नहीं सोचते हैं। चलो शुरू करते हैं, आपने मेरे सवाल पर सवाल उठाया था, आपने कहा था कि मेरी रणनीति असफल होने की संभावना नहीं है, लेकिन अगर यह विफल हो जाती है तो यह बहुत नुकसान पहुंचाएगा, है ना?

मैं: हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ, हाँ

S: अच्छा, आप सोचें कि मैं कैसे असफल हो सकता हूं। मेरे पास आमतौर पर लगभग 300 युआन हैं, जो मुझे 128 युआन के लिए समर्थन करने के लिए पर्याप्त है, जो कि 8 बार खेलना है। मेरी विफलता की एकमात्र संभावना यह है कि आठ बार लगातार सफेद हैं, और मैं समाप्त हो गया हूं।

मैं: ओह, यह बहुत कम संभावना है, लेकिन यह सच है … और यह बहुत नुकसान पहुंचाता है … ओह

S: आप गलत हैं, इस तरह की संभावना केवल गणित में मौजूद है. वास्तव में, यह संभव नहीं है कि मालिक इस तरह की स्थिति की अनुमति नहीं देता है. कल्पना कीजिए कि एक खेल में, एक ही रंग आठ बार दिखाई देता है, मेरे लिए स्वीकार्य है, क्योंकि मैंने इसे हजारों बार खेला है, आठ बार सफेद रंग की संभावना ¹⁄₁₂₈ है। लेकिन अन्य खिलाड़ियों के लिए जो कभी-कभी केवल एक बार खेलते हैं, वे क्या सोचेंगे, क्या वे स्वीकार करने के लिए तैयार हैं कि वे ¹⁄₁₂₈ भाग्य से टकरा गए हैं, या वे सट्टेबाज पर सवाल उठाने लगे हैं?

खेल को नियंत्रित करने के बारे में सवाल उठाने से रोकने के लिए, वास्तव में इसे नियंत्रित नहीं करना है, लेकिन यह सुनिश्चित करना है कि उन्हें ऐसा महसूस न हो।

इस सिद्धांत के आधार पर, यहां तक कि सामान्य वितरण की छोटी संभावनाओं को भी हटा दिया जाना चाहिए, क्योंकि वे सवाल उठाते हैं (क्योंकि निष्पक्षता के कारण यह अनुचित महसूस होता है) । इसके विपरीत, गर्म पानी में तले हुए मेंढक के रूप में कभी-कभी कुछ डिब्बे में हेरफेर किया जाता है, क्योंकि सज्जनों को पहले से पता नहीं है कि सफेद और काला एक अल्पसंख्यक है, इसलिए परिणामों के अनुसार, यह काले और सफेद के औसत वितरण को नहीं तोड़ता है।

इसलिए, सट्टेबाजों को कुछ लोगों को जीतने की अनुमति देने से कोई फर्क नहीं पड़ता, क्योंकि यह चाल एक अंतर्निहित काले और सफेद संतुलन को नहीं तोड़ती है। लेकिन यह बिल्कुल भी स्वीकार्य नहीं है कि एक ही रंग की पट्टियाँ लगातार दिखाई दें, हालांकि बड़ी संख्या में खेलों में ऐसी छोटी संभावनाएं होनी चाहिए।

वे गणित में छोटी संभावना की घटनाएं हैं, लेकिन वास्तविकता में उन्हें शून्य संभावना की घटनाओं के रूप में संशोधित किया गया है।

यहाँ मैं पूरी तरह से समझता हूँ कि एस वास्तव में कहाँ तेज है, और यह भी कि एक सरल रणनीति हमेशा इस तरह के एक निष्पक्ष खेल में कैसे जीत सकती है।

बाद में, एस ने कहा कि वह सोचता है कि मालिकों को जानबूझकर 10% राजस्व पर नियंत्रण करना बहुत परेशानी है, क्योंकि मालिकों को अन्य खेलों और खिलाड़ियों की भी देखभाल करनी है। इसलिए यह अनुमान लगाने के लिए अधिक निकट है कि यह मशीन स्वयं एक यादृच्छिक वितरण के साथ आती है। इस वितरण के तहत, मालिकों को वास्तव में राजस्व मिलता है और खिलाड़ियों के रूप में कुल मिलाकर, शून्य है। और मालिकों को हर दिन कुछ समय के लिए धूम्रपान करना पड़ता है, कुछ खेलों को हेरफेर करना पड़ता है, जिससे मालिकों को इन खेलों में पर्याप्त पैसा मिलता है, और अन्य समय में मशीन को स्वचालित रूप से चलाने के लिए छोड़ दिया जाता है।

और एस की रणनीति न केवल एक लालची मालिक के लिए काम करती है, बल्कि एक निष्पक्ष दिखने वाली मशीन के लिए भी परीक्षण की जाती है। यह बहुत सरल है, यह एक मशीन है जो एक दशक पहले की है, इसमें इलेक्ट्रॉनिक घटक हैं, लेकिन यह एक साधारण यांत्रिक उपकरण है। वास्तव में, कंप्यूटर सहित, कोई भी मशीन बनाने वाला वास्तव में यादृच्छिकता का प्रतिनिधित्व नहीं कर सकता है। किसी भी कार्यक्रम में यादृच्छिक संख्याएं मूल रूप से जटिल परिचालनों में एक छद्म यादृच्छिकता हैं। बेशक, कंप्यूटर की गणना की क्षमता बहुत मजबूत है, यह बहुत मजबूत है, जो लाखों स्थितियों का अनुकरण कर सकती है।

लेकिन एक साधारण मशीन के लिए, दर्जनों स्थितियों का अनुकरण करने के लिए बहुत अधिक लागत होती है, और यह मानने की कोई आवश्यकता नहीं है कि मशीन केवल ब्लैक ब्लैक ब्लैक ब्लैक, व्हाइट ब्लैक ब्लैक, व्हाइट ब्लैक ब्लैक, व्हाइट ब्लैक ब्लैक …

एस के लिए, यदि मशीन केवल 32 स्थितियों को पूर्व-बनाए रखती है और उन्हें बार-बार बुलाती है, तो उसकी रणनीति हमेशा जीतने के लिए पर्याप्त है, जब तक कि वह पांच बार दांव लगाने के लिए तैयार न हो, 1 + 2 + 4 + 8 + 16 = 31 युआन।

वास्तव में, एस ने पहली बार में 30 से अधिक सिक्के खरीदे थे। हर बार इन सिक्कों के साथ पूंजी के रूप में, अतिरिक्त 20-30 सिक्के कमाने के बाद, वह वास्तव में खेलना चाहता था। यानी, मशीन की पूर्ति 32 घंटे के बराबर से कम है।

तब मुझे पता चला कि मेरे और एस की सोच में कितना अंतर है, मेरे सभी निर्णय गणित पर आधारित हैं, और यह हिस्सा पहले के दो-तीन सौ शब्दों में हल किया गया था, लेकिन बाद के हजारों शब्द वह क्षेत्र हैं जो एस वास्तव में सोचता है।

मैं इस वीडियो को पहली बार देख रहा हूं और मुझे लगता है कि यह मेरे लिए एक तरह से गर्भपात है!

आखिरकार, यह खेल है, और मैं पहले से ही संख्याओं की एक मात्रात्मक दुनिया में डूब गया हूं, एक ऐसी रणनीति की तलाश कर रहा हूं जो अधिक लाभ की उम्मीद कर सकती है, और एक बहुत ही बुनियादी तथ्य की अनदेखी कर रही है जो कि हमारे सामने है:

सट्टा व्यापार मांस और रक्त के साथ लोगों के साथ खेल रहा है! मात्रा हमेशा केवल साधन और विधि है, व्यापारियों के बाद सभी लोगों के साथ व्यापार कर रहे हैं. तथाकथित व्यापार, एक व्यापार प्रतिद्वंद्वी औ