Dalam artikel ini, kita akan menguraikan proses Ornstein-Uhlenbeck, menjelaskan rumus matematisnya, mengimplementasikannya dan mensimulasinya dengan Python, dan membahas beberapa aplikasi praktisnya dalam keuangan kuantitatif dan sistem perdagangan. Kita akan menggunakan model proses acak yang lebih canggih, yang disebut proses Ornstein-Uhlenbeck (OU), yang dapat digunakan untuk memodelkan urutan waktu regresi yang menunjukkan perilaku nilai rata-rata. Ini sangat berguna untuk memodelkan suku bunga dalam penetapan harga derivatif dan untuk melakukan algoritma pada sistem perdagangan saat perdagangan.

Apa itu Proses Ornstein-Uhlenbeck?

Proses Ornstein-Uhlenbeck adalah sebuah proses acak waktu yang terus menerus yang digunakan untuk memodelkan perilaku regresi nilai rata-rata. Ini berarti bahwa, berbeda dengan standar random walk atau gerakan Brownian yang dapat mengapung tanpa batas, proses OU cenderung kembali ke rata-rata jangka panjang dari waktu ke waktu. Secara matematis, proses OU adalah solusi dari persamaan diferensial acak tertentu (SDE) yang mengontrol perilaku regresi nilai rata-rata ini.

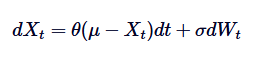
Di antaranya, Xt adalah proses acak pada waktu t, μ adalah rata-rata jangka panjang, θ adalah tingkat pengembalian rata-rata, δ adalah volatilitas, dan dWt adalah proses Wiener atau gerakan Brown standar.

Latar Belakang Sejarah dan Aplikasi

Proses Ornstein-Uhlenbeck pertama kali dikemukakan oleh Leonard Ornstein dan George Eugene Uhlenbeck pada tahun 1930 untuk mensimulasikan kecepatan partikel yang melakukan gerakan Brownian dalam keadaan bergesekan. Seiring berjalannya waktu, kepraktisan proses ini telah melampaui bidang fisika, dengan aplikasi di berbagai bidang seperti biologi, kimia, ekonomi, dan keuangan.

Dalam keuangan kuantitatif, proses OU sangat berguna untuk memodelkan fenomena yang menunjukkan perilaku regresi rata-rata. Contoh yang menonjol meliputi volatilitas suku bunga, nilai tukar, dan pasar keuangan. Misalnya, model suku bunga populer, model Vasicek, berasal langsung dari proses OU.

Pentingnya dalam keuangan kuantitatif

Proses Ornstein-Uhlenbeck sangat penting dalam keuangan kuantitatif karena: sifat regresi rata-ratanya yang membuatnya menjadi pilihan alami untuk memodelkan variabel keuangan yang tidak menunjukkan pergerakan acak, tetapi berfluktuasi rata-rata jangka panjang di sekitar stabilitas. Karakteristik ini sangat penting untuk pemodelan suku bunga, di mana regresi rata-rata mencerminkan pengaruh bank sentral terhadap tingkat suku bunga stabil jangka panjang.

Selain itu, proses OU juga digunakan dalam model harga aset (termasuk penilaian derivatif) dan strategi manajemen risiko. Ini juga dapat digunakan sebagai blok bangunan model yang lebih kompleks, seperti model Cox-Ingersoll-Ross (CIR), yang memperluas proses OU untuk memodelkan suku bunga dengan nilai non-negatif.

Fitur utama dan intuisi

Fitur utama dari proses Ornstein-Uhlenbeck dapat diringkas sebagai berikut:

• Regressi rata-rata:Proses OU cenderung kembali ke rata-rata jangka panjang μ. Ini kontras dengan proses seperti gerakan Brown, yang tidak menunjukkan kecenderungan ini.
• Volatilitas:Parameterδ tingkat randomitas atau volatilitas dalam proses kontrol. Semakin volatilitas, semakin besar proses menyimpang dari rata-rata sebelum regresi.
• Kecepatan kembali:Parameter θ menentukan kecepatan proses kembali ke rata-rata.
• Stabilitas:Proses OU bersifat stabil, yang berarti sifat statistiknya tidak berubah seiring waktu. Hal ini sangat penting untuk memodelkan sistem stabilitas di bidang keuangan.

Secara intuitif, Anda dapat memodelkan proses Ornstein-Uhlenbeck sebagai perilaku otot kalsium yang membentang di sekitar nilai rata-rata. Meskipun prosesnya mungkin menyimpang dari rata-rata karena fluktuasi acak, batang ketegangan otot kalsium (seperti regresi rata-rata) memastikannya akhirnya kembali ke rata-rata.

Perbandingan dengan proses acak lainnya

Karena proses OU terkait erat dengan pemodelan berbagai fenomena keuangan, maka seringkali dibandingkan dengan proses acak lainnya (seperti Gerakan Brown dan Gerakan Brown Geometri (GBM)). Berbeda dengan Gerakan Brown (yang tidak memiliki kecenderungan untuk kembali ke rata-rata), proses OU memiliki perilaku yang jelas untuk kembali ke rata-rata. Hal ini membuatnya lebih cocok untuk pemodelan skenario di mana variabel berputar di sekitar pergerakan keseimbangan yang stabil.

Dibandingkan dengan GBM, yang biasanya digunakan untuk memodelkan harga saham dan mengandung item drift dan fluktuasi, proses OU tidak menunjukkan pertumbuhan indeks, tetapi bergoyang di sekitar rata-ratanya. GBM lebih cocok untuk memodelkan jumlah yang meningkat dari waktu ke waktu, sedangkan proses OU sangat cocok untuk memodelkan variabel yang menampilkan karakteristik kemunduran rata-rata.

Contoh keuangan kuantitatif

Proses Ornstein-Uhlenbec memiliki aplikasi yang luas di bidang keuangan, terutama dalam skenario pemodelan dengan regressi rata-rata sebagai fitur kunci. Di bawah ini, kita akan membahas beberapa kasus penggunaan yang paling umum.

Pemodelan suku bunga

Salah satu aplikasi yang paling menonjol dari proses OU adalah pemodelan tingkat bunga, terutama dalam kerangka model Vasicek. Model Vasicek mengasumsikan bahwa tingkat bunga mengikuti proses OU, yaitu tingkat bunga cenderung kembali ke rata-rata jangka panjang dari waktu ke waktu. Ciri ini sangat penting untuk mensimulasikan dengan akurat perilaku tingkat bunga, karena tingkat bunga cenderung tidak berfluktuasi tanpa batas waktu, tetapi berfluktuasi di sekitar tingkat rata-rata yang dipengaruhi oleh kondisi ekonomi.

Penetapan harga aset

Dalam penilaian aset, terutama sekuritas dengan pendapatan tetap, proses OU sering digunakan untuk mensimulasikan evolusi tingkat pengembalian obligasi. Sifat regresi rata-rata dari proses OU memastikan bahwa tingkat pengembalian tidak terlalu jauh dari rata-rata historisnya, yang sesuai dengan perilaku pasar yang diamati. Hal ini membuat proses OU menjadi alat yang berharga untuk penetapan harga obligasi dan instrumen sensitif tingkat bunga lainnya.

Strategi perdagangan pasangan

Pairing trading adalah strategi netral pasar yang melibatkan pembentukan posisi offset di antara dua aset terkait. Dalam hal ini, proses OU sangat berguna karena dapat memodelkan perbedaan harga antara dua aset, yang biasanya merupakan nilai rata-rata. Dengan menggunakan proses OU untuk memodelkan perbedaan harga, pedagang dapat mengkonfirmasi titik masuk dan keluar yang menguntungkan ketika harga menyimpang dari nilai rata-ratanya, memprediksi nilai rata-rata, dan menghasilkan sinyal perdagangan.

Sebagai contoh, jika selisih harga antara dua futures melonjak melampaui suatu titik terendah, trader mungkin akan melakukan shorting pada futures yang berkinerja baik dan melakukan multiply pada futures yang berkinerja buruk, dengan harapan selisih harga akan kembali ke level rata-rata historisnya, sehingga menghasilkan keuntungan ketika terjadi pembalikan.

Solusi untuk Ornstein-Uhlenbeck SDE

Ornstein-Uhlenbeck proses persamaan diferensial adalah dasar dari pemecahan SDE. Untuk memecahkan SDE, kita menggunakan integrasi faktorisasi. Mari kita tuliskan SDE:

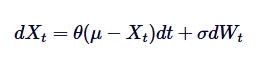
Pertama, kita kalikan kedua sisi dengan faktor integrasi /upload/asset/28dfe9abfb54772651590.png:

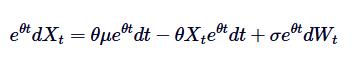
Perhatikan bahwa jika kita menambahkan 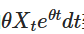di kedua sisi, maka sisi kiri dapat dinyatakan sebagai perkalian dari perkalian:

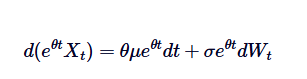
Dengan mengintegrasikan kedua sisi dari 0 ke t, kita mendapatkan:

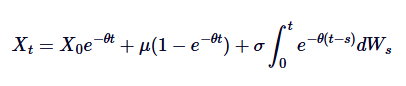
Ini adalah definisi umum dari Ornstein-Uhlenbeck SDE.

Solusi eksplisit yang diimplementasikan di atas memiliki beberapa implikasi penting. Bagian pertama 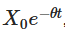menunjukkan bahwa nilai awal menurun seiring waktu, menunjukkan bagaimana proses secara bertahap melupakan titik awal. Bagian kedua 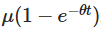menunjukkan bahwa proses cenderung ke nilai rata-rata μ seiring waktu.

Solusi ini menekankan keseimbangan antara perilaku pengembalian nilai rata-rata pasti dan faktor acak yang didorong oleh gerakan Brownian. Pemahaman tentang solusi ini sangat penting untuk mensimulasikan proses OU secara efektif, seperti yang dijelaskan di bawah ini.

Hubungan dengan proses acak lainnya

Proses Ornstein-Uhlenbeck memiliki beberapa hubungan penting dengan proses acak terkenal lainnya (termasuk gerakan Brown dan model Vasicek).

Hubungan dengan gerakan Brown

Proses Ornstein-Uhlenbeck dapat dilihat sebagai versi regression rata-rata dari gerakan Brownian. Gerakan Brownian menggambarkan sebuah proses dengan peningkatan independen dan tidak ada tren regression rata-rata, sedangkan proses OU menggunakan modifikasi drift untuk memperkenalkan regression rata-rata dari gerakan Brownian, sehingga menarik proses kembali ke nilai pusat. Secara matematis, jika kita menetapkanθ = 0, proses OU akan disederhanakan menjadi gerakan Brownian standar dengan gelombang:

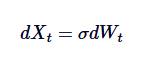
Oleh karena itu, gerakan Brownian adalah contoh khusus dari proses OU, yang sesuai dengan hilangnya regresi rata-rata.

Hubungan dengan model Vasicek

Model Vasicek digunakan secara luas dalam pemodelan suku bunga, pada dasarnya adalah proses Ornstein-Uhlenbeck dalam evolusi suku bunga. Model Vasicek mengasumsikan suku bunga mengikuti proses OU, di mana SDE didefinisikan sebagai:

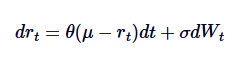
Di antaranya, rt menunjukkan tingkat bunga jangka pendek, dan interpretasi parameter θ, μ, danδ mirip dengan interpretasi dalam proses OU. Model Vasicek mampu menghasilkan jalur nilai rata-rata bunga yang kembali, yang merupakan salah satu keunggulan utama dalam pemodelan keuangan.

Memahami hubungan ini dapat memberikan pemahaman yang lebih luas tentang bagaimana proses OU digunakan dalam berbagai lingkungan, terutama di bidang keuangan. Kami akan membahas hubungan ini secara praktis ketika membahas contoh aplikasi di bawah ini.

Proses Ornstein-Uhlenbeck dimodelkan dengan Python

Pada bagian ini, kita akan membahas bagaimana menggunakan Python untuk mensimulasikan proses Ornstein-Uhlenbeck (OU). Ini melibatkan penggunaan Euler-Maruyama dissociation untuk dissociate definisi proses OU (SDE) dari persamaan diferensial acak.

Disintegrasi SDE

Mari kita lihat kembali rumus-rumus matematika SDE di atas dan jelaskan setiap istilah:

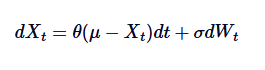
di dalam,

• Xt adalah nilai proses pada waktu t.
• θ adalah kecepatan regresi rata-rata
• μ adalah rata-rata jangka panjang dari proses tersebut.
• δ adalah parameter fluktuasi.
• dWt menunjukkan peningkatan proses Wiener (gerakan Brown standar).

Untuk mensimulasikan proses ini di komputer, kita perlu melakukan disassociation dari SDE waktu berkelanjutan. Salah satu metode yang umum digunakan adalah disassociation Euler-Maruyama, yang memperkirakan proses berkelanjutan dengan mempertimbangkan langkah waktu berkelanjutan yang kecil.

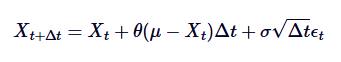
Di antaranya, 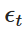adalah variabel acak yang diekstrak dari distribusi normal standar (yaitu 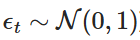). Disassociasi ini memungkinkan kita untuk menghitung nilai Xt secara iteratif dari waktu ke waktu, sehingga mensimulasikan perilaku proses OU.

Implementasi Python

Sekarang mari kita implementasikan proses Ornstein-Uhlenbeck yang terisolasi dengan Python. Dalam konteks ini, kita hanya menggunakan NumPy dan Matplotlib Python library.

Pertama, kita mengimpor NumPy dan Matplotlib dengan cara standar. Kemudian, kita menentukan semua parameter untuk model OU. Kemudian, kita terlebih dahulu mengalokasikan array NumPy dengan panjang N, untuk menambahkannya setelah menghitung jalur OU. Kemudian kita mengulangi langkah N-1 (langkah 1 adalah kondisi awal yang ditentukan X0), mensimulasikan peningkatan acak dW, dan kemudian menghitung iterasi berikutnya dari jalur OU berdasarkan rumus matematika di atas.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Hasil pemetaan adalah sebagai berikut:

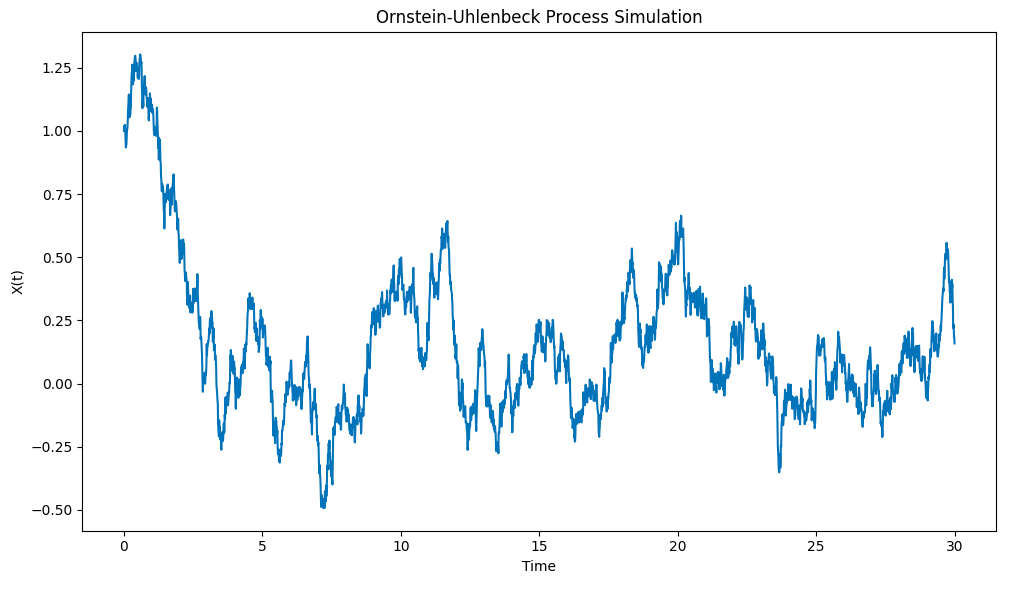
Simulasi proses Ornstein-Uhlenbeck dengan Python

Perhatikan bagaimana proses ini dengan cepat mengambil X0 = 1 dari kondisi awal ke nilai rata-rata μ = 0, dan kemudian ketika ia menyimpang dari nilai rata-rata itu, ia menunjukkan kecenderungan untuk kembali ke nilai rata-rata itu.

Ringkasan dan langkah selanjutnya

Dalam artikel ini, kami menguraikan proses Ornstein-Uhlenbeck, menjelaskan rumus matematika, dan memberikan implementasi dasar Python untuk mensimulasikan versi terpisah dari SDE waktu kontinu. Dalam artikel berikutnya, kami akan mempelajari SDE yang lebih kompleks yang dibangun berdasarkan proses OU dan bagaimana mereka digunakan dalam sistem perdagangan dan aplikasi harga derivatif.

Kode lengkap

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Sumber: http://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/