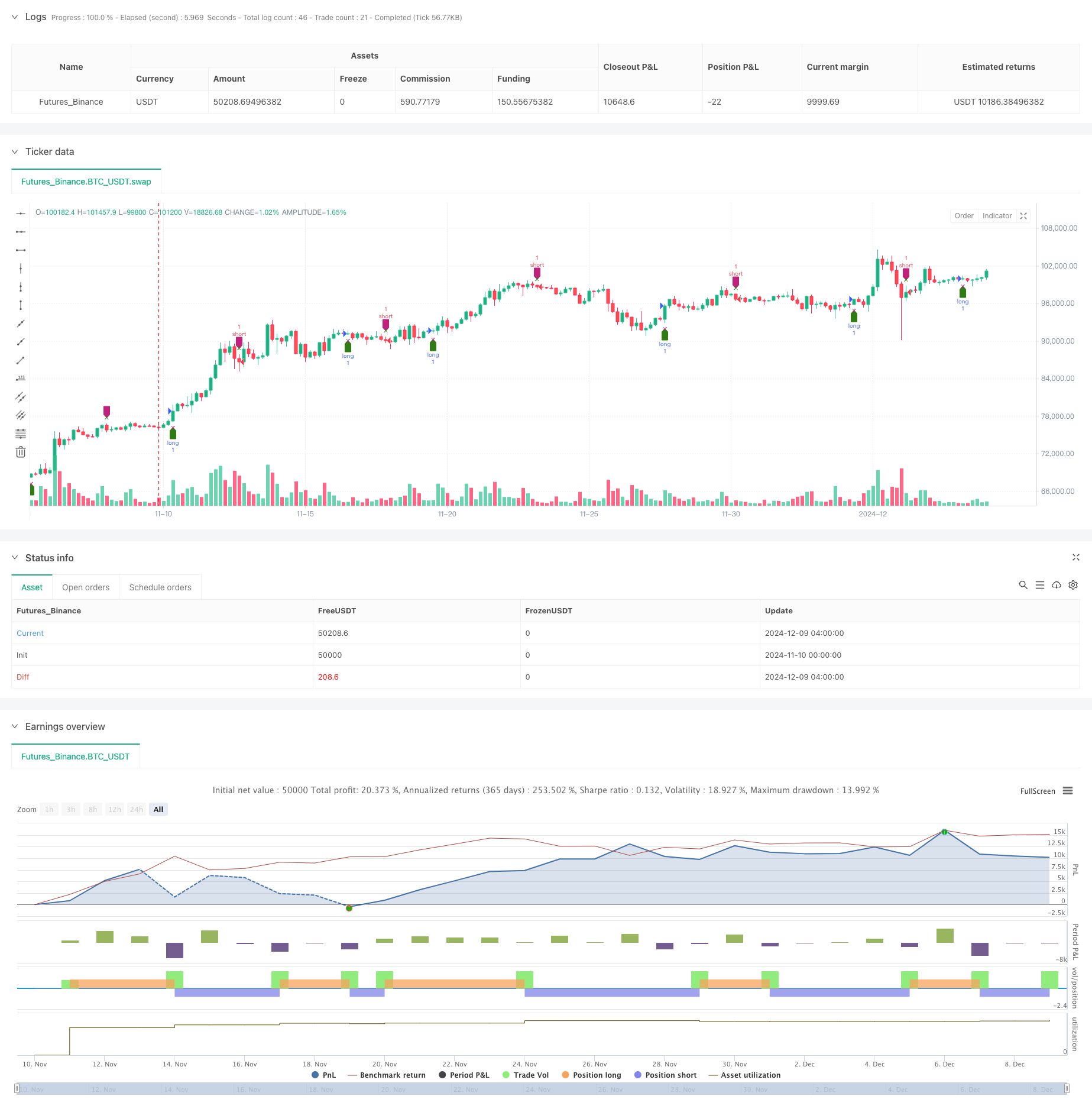
Strategi ini adalah sistem perdagangan kuantitatif yang didasarkan pada osilator dinamis RSI. Dengan melakukan analisa multifungsi dan urutan waktu dari indikator RSI, strategi ini menghitung tingkat perubahan RSI untuk menangkap dinamika pasar. Strategi ini menggunakan metode matematika canggih seperti pemecahan QR untuk pemrosesan sinyal, dan untuk pengambilan keputusan perdagangan yang digabungkan dengan sistem linier.

Prinsip Strategi

Inti dari strategi ini adalah Delta-RSI oscillator, yang diimplementasikan melalui langkah-langkah berikut:

1. Pertama, menghitung RSI tradisional sebagai data dasar.
2. RSI ditangani dengan multifungsi untuk mengurangi kebisingan
3. Perhitungan variabel waktu RSI yang diperoleh dari Delta-RSI, yang mencerminkan tingkat perubahan RSI
4. Membandingkan Delta-RSI dengan rata-rata bergerak untuk menghasilkan sinyal perdagangan
5. Evaluasi dan penyaringan kualitas kecocokan menggunakan kesalahan akar rata (RMSE)

Sinyal perdagangan dapat dihasilkan dengan tiga cara:

• Jalur nol: Delta-RSI lebih tinggi dari nilai negatif dan lebih rendah dari nilai positif
• Garis sinyal bersilang: Delta-RSI naik / turun di atas rata-rata bergerak masing-masing
• Pergeseran arah: Delta-RSI melakukan over saat zona negatif mulai naik, melakukan over saat zona positif mulai turun

Keunggulan Strategis

1. Dasar matematika yang kuat: menggunakan metode matematika canggih seperti pemecahan QR untuk pemrosesan sinyal, dasar teoritis yang solid
2. Signal Smoothing: Fitting multi-modal dapat secara efektif menyaring kebisingan pasar, meningkatkan kualitas sinyal
3. Fleksibel: menyediakan berbagai cara menghasilkan sinyal dan pilihan parameter untuk menyesuaikan dengan lingkungan pasar yang berbeda
4. Risiko terkontrol: berisi mekanisme penyaringan RMSE, yang dapat memfilter sinyal dengan keandalan yang lebih tinggi
5. Efisiensi komputasi: Operasi matriks menggunakan algoritma yang dioptimalkan, dengan efisiensi operasi yang lebih tinggi

Risiko Strategis

1. Parameter sensitif: beberapa parameter kunci yang perlu disesuaikan dengan baik, dan pilihan parameter yang tidak tepat dapat berdampak buruk pada kinerja strategi
2. Lag: Proses sinyal yang lancar dapat menyebabkan keterlambatan, dan mungkin kehilangan kecepatan.
3. False breakout: kemungkinan sinyal palsu dalam pasar yang bergejolak, meningkatkan biaya transaksi
4. Kompleksitas komputasi: melibatkan lebih banyak operasi matriks, dan kemungkinan adanya hambatan kinerja dalam perdagangan frekuensi tinggi
5. Overfitting: Perhatian harus diberikan untuk menghindari overfitting data historis saat mengoptimalkan parameter

Arah optimasi strategi

1. Parameter penyesuaian diri: dapat menyesuaikan siklus RSI dan tingkat penyesuaian sesuai dengan dinamika fluktuasi pasar
2. Siklus multi waktu: sinyal yang menggabungkan lebih banyak siklus waktu untuk verifikasi silang
3. Filter fluktuasi: menambahkan indikator fluktuasi seperti ATR untuk filter sinyal
4. Klasifikasi pasar: menggunakan aturan pembuatan sinyal yang berbeda untuk kondisi pasar yang berbeda (trend/shake)
5. Optimasi Stop Loss: Menambahkan mekanisme stop loss yang lebih cerdas, seperti stop loss dinamis berdasarkan titik resistensi pendukung

Meringkaskan

Ini adalah strategi perdagangan kuantitatif dengan struktur yang utuh dan dasar teoritis yang kuat. Dengan analisis karakteristik dinamis RSI, pengolahan sinyal dikombinasikan dengan metode matematika modern, dapat menangkap tren pasar dengan lebih baik. Meskipun ada beberapa masalah sensitivitas parameter dan kompleksitas komputasi, tetapi dengan pilihan dan pengoptimalan parameter yang masuk akal, strategi ini memiliki nilai aplikasi yang baik.