1. フォーラム
  2. 量子ペディア
  3. SPY と IWM の間の日中逆転対戦略のバックテスト

SPY と IWM の間の日中逆転対戦略のバックテスト

作者: リン・ハーン優しさ作成日:2019年3月28日 10:51:06 更新日:

この記事では,最初のイントラデイ・トレーディング戦略について説明します. クラシックなトレーディング・アイディアである"取引ペア"を使用します. この例では,ニューヨーク証券取引所 (NYSE) で取引されている2つのエクスチェンジ・トレード・ファンド (ETF) SPYとIWMを使用し,それぞれS&P500とラッセル2000の米国株式市場指数を表現しようとします.

この戦略は,一般的に,ETFのペア間の幅を1つを長引いて,もう1つの金額をショートすることで創出する. 長期対短期の比率は,統計的コインテグレーション時間列技術などの多くの方法で定義することができます. このシナリオでは,SPYとIWMの間のヘッジ比をローリング線形回帰によって計算します. これにより,SPYとIWMの間の幅を創出することができ,zスコアに標準化されます. zスコアが特定の値を超えると,トレードシグナルが生成されます.

この戦略の根拠は,SPYとIWMが大概同じ状況,つまり大資本と小資本の米国企業の経済を特徴づけていることである.前提は,価格のスプレッドを取ると,それは平均を逆転するものであるべきである.S&P500またはラッセル2000指数 (小資本/大資本差,再バランス日付またはブロックトレードなどの) にそれぞれ影響を与える場合 (S&P500またはラッセル2000指数など),両者の長期価格シリーズはおそらく統合される.

戦略

戦略は次の段階で行われます.

  1. SPYとIWMのデータ - 1分バーは,2007年4月から2014年2月までの期間で得られる.
  2. 処理 - データは正しく並べられ,欠けているバーは相互に取り消されます.
  3. スプレッド - 2つのETF間のヘッジ比は,ローリング線形回帰を取ることで計算される.これは,回帰係数を1バー前に移動し,回帰係数を再計算するバックバックウィンドウを使用してβ回帰係数として定義される.したがって,バーbiのヘッジ比βiは,kバーのバックバックのために,点bi−1−kからbi−1を横断して計算される.
  4. Zスコア - スプレッドの標準スコアは通常の方法で計算されます.これは,スプレッドの (サンプル) 平均を引いて,スプレッドの (サンプル) 標準偏差で割ることを意味します. zスコアが無次元量であるため,スリース値パラメータをより直接的に解釈できるようにする理由です.私は意図的に計算にルーカヘッドバイアスを導入しました.それがどれほど微妙であるかを示すために.試してみて注意してください!
  5. トレーディング - 負のzスコアが既定 (または後最適化) 値を下回るときにロング信号が生成され,ショート信号はその逆である. 絶対のzスコアが追加の値を下回るときにアウトシグナルが生成される. この戦略のために,私は (少し恣意的に) 絶対のエントリースロングレスを ┃z ┃z ┃z=2と終了スロングレスを ┃z ┃z ┃z=1と選択した. 平均の逆転行動を想定して,この関係は把握され,ポジティブなパフォーマンスを提供することを期待する.

おそらく,戦略を深く理解する最良の方法は,実際にそれを実装することです. 次のセクションでは,この平均逆転戦略の実装のための完全な Python コード (単一のファイル) を説明しています.理解を助けるために,私は自由にコードにコメントしました.

Python の実装

Python/pandaのチュートリアルと同様に,このチュートリアルで説明されているように Python 研究環境を設定する必要があります. セットアップすると,最初のタスクは必要な Python ライブラリをインポートすることです. このバックテストのために matplotlib と pandas が必要です.

私が使用している特定のライブラリバージョンは以下の通りです.

  • パイソン - 2.7.3
  • NumPy - 1.8.0
  • パンダ 0.12.0
  • マットプロットリブ - 1.1.0 図書室をインポートしてみましょう
# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

次の関数 create_pairs_dataframe は,2つのシンボルのイントラデイバーを含む2つの CSV ファイルをインポートします.私たちの場合,これは SPY と IWM です.その後,2つのオリジナルファイルのインデックスを使用する別々のデータフレームペアを作成します.そのタイムスタンプが見逃した取引やエラーのために異なる可能性が高いため,これは一致するデータを持つことを保証します. これはパンダのようなデータ分析ライブラリを使用する主な利点の1つです. ボイラープレートコードは非常に効率的に処理されます.

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

次のステップは,SPY と IWM の間のローリング線形回帰を実行することです.この例では,IWM は予測値 (x) で,SPY は応答値 (y) です.私は 100 バーのデフォルトのバックバックウィンドウを設定しました.上記のように,これは戦略のパラメータです.戦略が堅牢であるとみなされるためには,理想的にはバックバック期の凸関数としてリターンプロファイル (または他のパフォーマンス測定値) を見たいと思います.したがって,コードの後段階では,バックバック期を範囲にわたって変えて感度分析を行います.

SPY-IWMの線形回帰モデルでローリングベータ係数が計算されると,それを DataFrame のペアに追加し,空欄を削除します.これはトリミングメーターとしてlookback のサイズに等しい最初のバーセットを構成します.その後,SPY の単位と -βi の単位として2つのETFのスプレッドを作成します.これは明らかに現実的な状況ではありません.これは実際の実装では不可能です.

最後に,スプレッドの平均を減算して標準偏差で正規化することで計算されるスプレッドのzスコアを作成します.ここでかなり微妙な見出し偏差が発生していることに注意してください.研究でそのような間違いを犯すのがどれほど簡単かを強調したいので,意図的にコードに残しました.平均値と標準偏差は,スプレッド時間系列全体に計算されます.これが真の歴史的精度を反映するなら,この情報は,暗黙に将来の情報を使用しているため,入手できないでしょう.したがって,私たちはローリング平均値とstdevを使用してzスコアを計算する必要があります.

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

create_long_short_market_signalsでは,トレード信号が作成されます.これらの信号は,zスコアがマイナス zスコアを超えるとスプレッドをロングし,zスコアがマイナス zスコアを超えるとスプレッドをショートして計算されます.出口信号は,zスコアの絶対値が他の (大きさの小さい) 限界値未満またはそれと同等であるときに与えられます.

この状況を達成するためには,各バーに対して,戦略が市場内または外にあるかどうかを知る必要があります. long_marketと short_marketは,ロングとショート市場のポジションを追跡するために定義された2つの変数です.残念ながら,これはベクトル化されたアプローチとは対照的に繰り返す方法でコードするのがはるかに簡単で,計算は遅いです. CSV ファイルごとに ~ 700,000 データポイントを必要とする 1 分間のバーにもかかわらず,それはまだ私の古いデスクトップマシンで計算するのに比較的速いです!

パンダの DataFrame を繰り返すには (一般的な操作ではない) iterrows メソッドを使用する必要があります. このメソッドは,繰り返すためのジェネレーターを提供します.

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

この段階では,実際のロング/ショートシグナルを含むペアを更新し,市場に入れる必要があるかどうかを決定することができます.現在,ポジションの市場価値を追跡するためにポートフォリオを作成する必要があります.最初のタスクは,ロングとショートシグナルを組み合わせるポジション列を作成することです.これは (1,0,−1),1から要素を表示し,1はロング/マーケットポジション,0はポジションがないことを表し (退出すべき),−1はショート/マーケットポジションを表します. sym1と sym2列は各バーの終了時にSPYとIWMポジションの市場価値を表します.

ETFの市場価値が作成されると,各バーの終わりに総市場価値を生成するためにそれらを合計します.これは,そのシリーズオブジェクトの pct_change 方法によってリターンストリームに変換されます.次のコード行は悪いエントリ (NaN と inf 要素) をクリアし,最終的に完全な株式曲線を計算します.

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

について主要機能がすべてをまとめる. 日中の CSV ファイルは datadir パଥରେ位置しています. 特定のディレクトリを指すために下記のコードを変更してください.

ストラテジーはバックバック期間にどの程度敏感かを判断するには,バックバックの範囲のパフォーマンスメトリックを計算する必要があります.私はパフォーマンスメーターとしてポートフォリオの最終的な総百分比リターンを選択し,バックバックの範囲は [50,200] で,10のインクリメントで選択しました.次のコードでは,以前の関数はこの範囲全体で forループに包まれ,他の値が固定されています.最終タスクは,バックバックとリターンの線グラフを作成するためにmatplotlibを使用することです:

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

Lookback Period vs Returns のグラフは,現在見ることができます.Lookback の周りに 110 バーに等しい 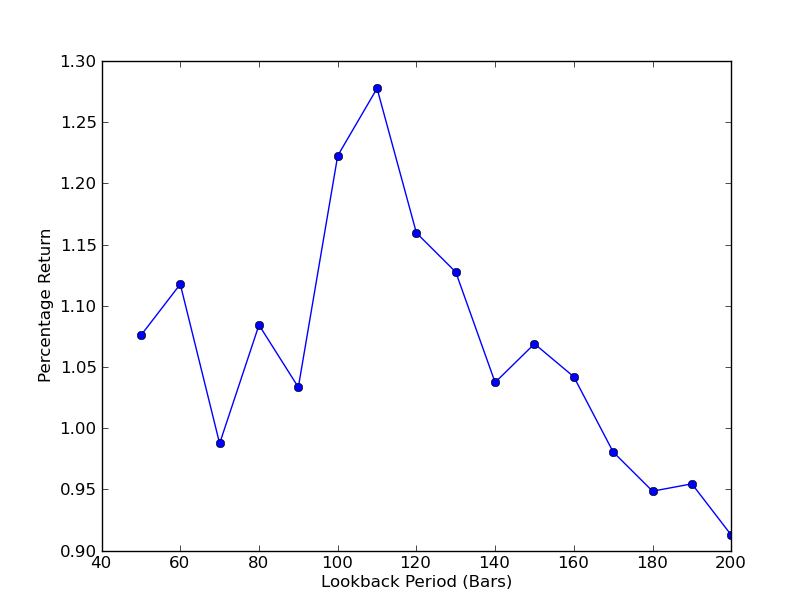global の最大値があることに注意してください.Lookback がリターンから独立している状況を見ていたら,これは懸念の理由になっていたでしょう.imgSPY-IWM 線形回帰によるヘッジ比回顧期間の感度分析

バックテストの記事は,上向き傾斜の株式曲線なしには完結しない.したがって,累積収益対時間の曲線をプロットしたい場合は,次のコードを使用できます.それはバックバックパラメータ研究から生成された最終ポートフォリオをプロットします.したがって,どのチャートを視覚化したいかに基づいてバックバックを選択する必要があります.チャートは,比較を助けるために同じ期間のSPYの収益もプロットします:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

次の株式曲線グラフは100日間の回顧期間のものです.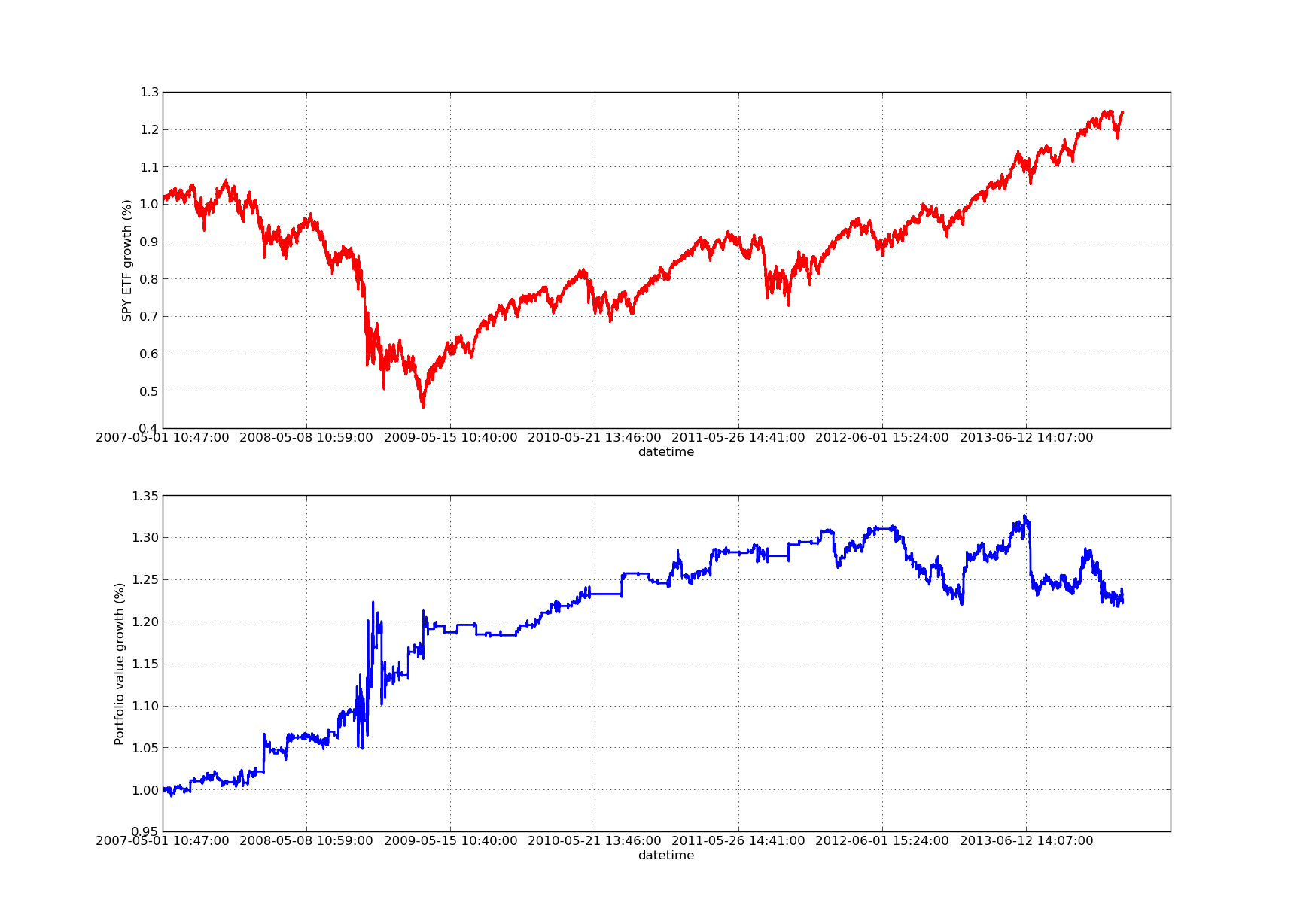imgSPY-IWM 線形回帰によるヘッジ比回顧期間の感度分析

2009年の金融危機期間中にSPYの引き上げが著しいことに注意してください.この段階では戦略も不安定な期間がありました.また,S&P500指数に反映されるこの期間のSPYの強い傾向性により,過去1年間で業績が若干悪化したことを注意してください.

差のzスコアを計算する際には,まだlookheadバイアスを考慮しなければならないことに注意してください.さらに,これらの計算はすべて取引コストなしで実施されています.これらの要因を考慮すると,この戦略は確かに非常に劣悪なパフォーマンスを発揮します.手数料,オファー/オールスプレッドおよびスリップは,現在すべて考慮されていません.さらに,戦略はETFの割引単位で取引されています.これは非常に非現実的です.

この要因を考慮し,株式率曲線と業績指標に対する信頼を大幅に高めます. 投資のコストは,

もっと

2019 FMZ - すべての権利は保護されています.