SVM ベクトル マシンで賭け (取引) することでゴリラを追い抜くことができますか?

今日,我々は,金融界で最も恐ろしいライバルの一つであるオオカミを倒すために全力を尽くします. 賭けを賭けて50%の確率で勝てるオオカミを倒すのは,大変なことだと思います. 矢量分類器を支える機械学習のアルゴリズムを使用します.SVM矢量機械は,回帰と分類のタスクを解決する非常に強力な方法です.

• SVM 支持ベクトルマシン

SVMベクトルマシンは,次の考えに基づいています:超平面対pベクトル特征空間を用いることができる.SVMベクトルマシンのアルゴリズムは,超平面と識別マージンを用いて分類決定境界を作成する.

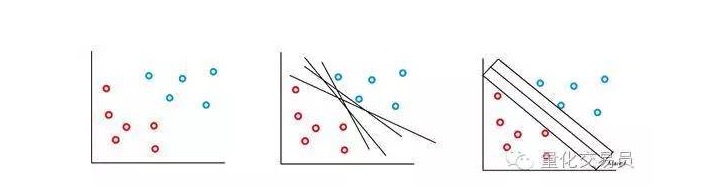
最も単純な場合,線形分類は可能である.アルゴリズムは決定境界を選択し,それはクラス間の距離を最大化することができる.

ほとんどの金融タイムシーケンスの場合,単純で線形的に分割可能な集合はほとんど見かけないが,分割できない集合はよく見かけます.SVMベクトルマシンは,ソフトマージンメソッド (soft margin method) と呼ばれる方法を実装することでこの問題を解決しました.

この例では,いくつかの誤った分類が許されるが,それらは自らが関数を実行し,C (コストまたは予算の誤りが許される) と正比の因数と誤りから境界までの距離を最小限に抑える.

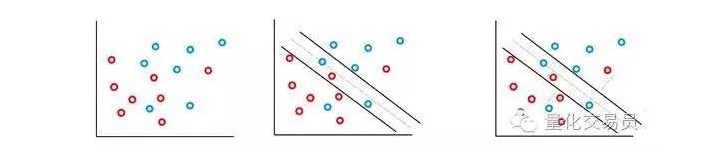
基本的に,機械は分類間の間隔を最大化し,Cが加重した罰項を最小限にします.

SVM分類器の素晴らしい特徴は,分類決定境界の位置とサイズが決定されるのは,決定境界から最も近い部分のみである.このアルゴリズムの特性により,遠隔の異常値の干渉に対抗できる.上図の青い点のように,決定境界への影響は小さい.

面白いのは,まだ始まったばかりだ.

赤い点と他の色の点を分離する:

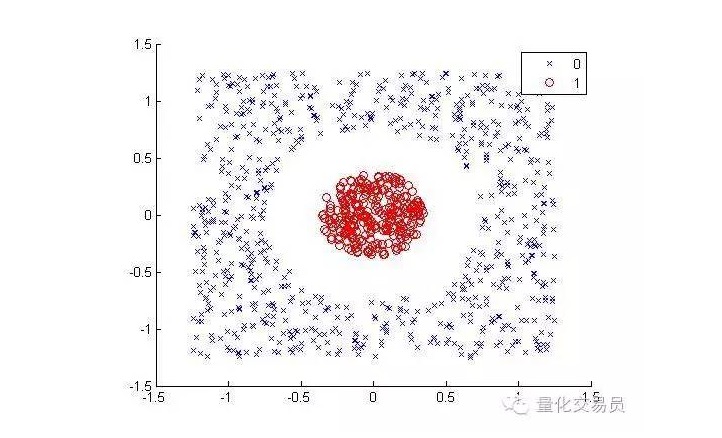
人間の目には,単純に分類できる (円線ならいい) でも,機械にとっては違います. 明らかに,直線にはなれない (一本の直線は赤い点を分けて見分けられない). ここで,内核の技をやってみよう.

内核技は,非常に巧妙な数学的技術で,高次元空間で線形分類問題を解くことができます. では,それがどのように行われているかを見てみましょう.

2次元特征空間を3次元に変換し,分類を完了すると2次元に戻します.

下は,拡大マッピングと分類完了後の図です.

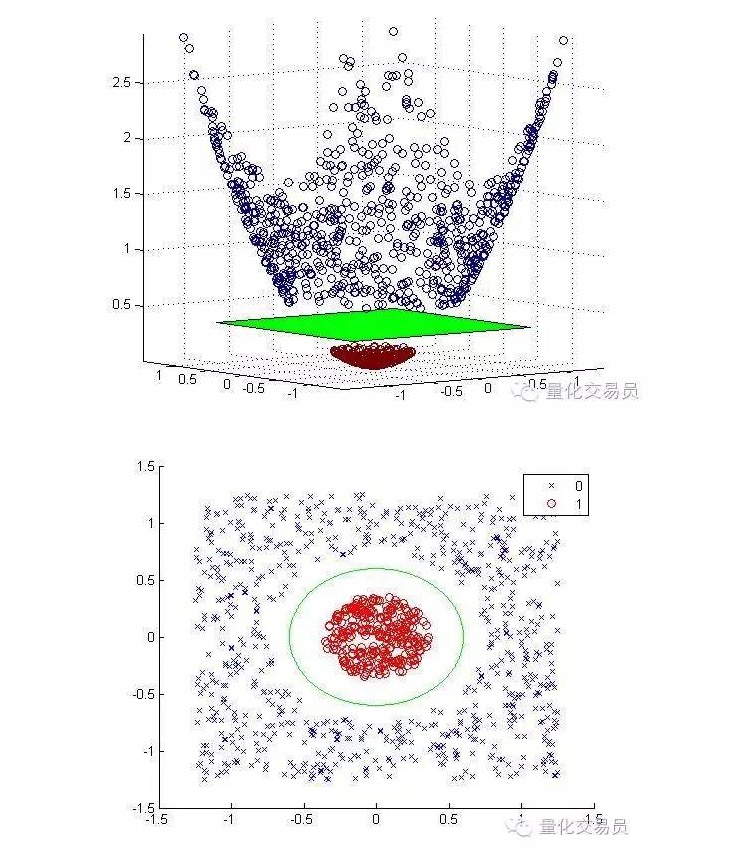
一般的に,dの入力がある場合,d次元入力空間からp次元特征空間へのマッピングを使用できます。上記の最小化アルゴリズムが生成するソリューションを実行し,元の入力空間のp次元超平面に戻します。

上記の数学的な解決の重要な前提は,特征空間で良い点サンプルセットをどのように生成するかによる.

境界の最適化を行うには,これらの点サンプルセットのみが必要で,マッピングは明示される必要がありません.高次元特征空間における入力空間の点は,核関数 ((と少しメルサー定理の助け) によって安全に計算できます.

例えば,あなたが,非常に大きな特性の空間で,あなたの分類問題を解決したいと仮定すると,それは100000次元です. あなたは,あなたが必要とする計算能力を想像できますか? 私はあなたがそれを行うことができるかどうか非常に疑っています.

• 挑戦とゴリラ

ジェフの予想力を打ち破る挑戦を準備中です. ジェフを見てみましょう.

ジェフは通貨市場の専門家で, ランダムに賭けることで50%の予測精度を得ることができました. この精度は,次の取引日の利回りを予測するシグナルです.

商品価格の時間帯など,様々な基本時間帯を使用し,各時間帯で10ラグの収益を上げ,合計55のフィーチャーを使用します.

私たちが構築するSVMベクトルマターは,3度カーネルの使用です. 適切なカーネルの選択は別の非常に困難な作業であり,CとΓのパラメータを校正するために,3倍クロス検証は,可能なパラメータの組み合わせのグリッド上で実行され,最良のセットが選択されます.

メディアは,この調査結果に不満を述べています.

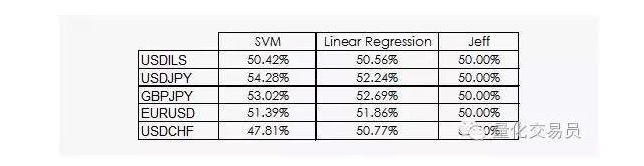
線形回帰とSVMのベクトルマシンがジェフを倒すのがわかります. 楽観的な結果ではありませんが,データから何かを抽出することもできます. これは良いニュースです. なぜなら,データ学科では,金融タイムシーケンスの日々の利益は最も有用ではないからです.

クロス検証後,データセットは訓練され,テストされ,訓練されたSVMの予測能力を記録し,安定したパフォーマンスを得るために,各通貨のランダム分割を1000回繰り返します.

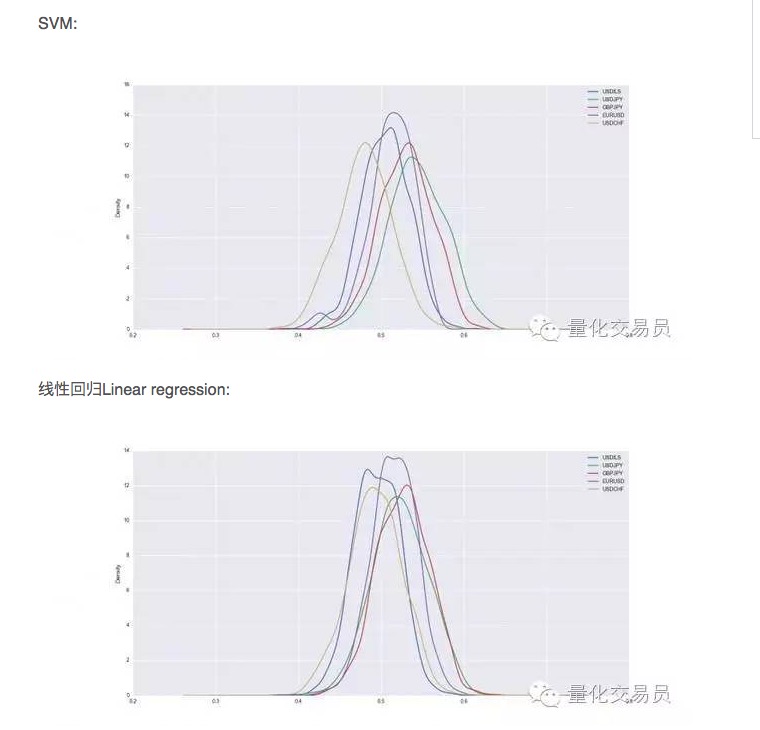
このように,SVMは単純な線形回帰よりも優れている場合もあるが,その性能の差も少し大きい.例えば,ドル対日元では,平均して予測可能な信号は,全体の54%を占めている.これはかなり良い結果ですが,もう少し詳しく見てみましょう!

テッドはジェフのいとこであり,もちろんゴリラでもあったが,ジェフよりずっと頭が良い.テッドは,ランダムな賭けではなく,トレーニングのサンプルセットを注視していた.彼の賭けの信号は,常にトレーニングのセットの最も一般的な出力から与えられていた.今,賢明なテッドを基準にしよう.

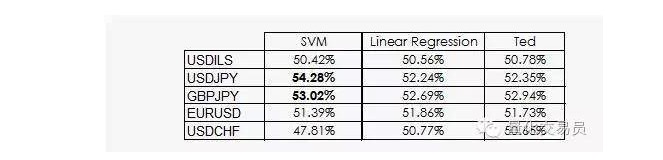
このように,SVMのほとんどのパフォーマンスは, 機械学習が分類を先行性と同等に扱う可能性が低いという事実にのみ由来する. 実際,線形回帰は特征空間から情報を得ることができないが, 切断点 (intercept) は回帰において有意義であり, 切断点とが特定の分類をよりよく表すという事実に関係している.

少し良いニュースですが,SVMベクトルマシーンがデータからいくつかの非線形情報を得ることができ,予測の精度を2%に提示することができます.

残念ながら,SVMのベクトルマシンには,その主な欠点があるように,それがどのような情報なのかは,まだ分かっていません.

投稿者:P. López 投稿者:P. López 投稿者:P. López 投稿者:P. López 微信公論号より転送