ネギとビッド・アスク・スプレッド：EKOPモデルの予備的研究

• #### 1 序言

最近は大変忙しくて,最後のコラムを書いてから数ヶ月が経ちました。この数か月間,多くのことが起こりました,そのうちのいくつかは,私自身の人生にとって,絶え間ない黒天でした。しかし,これらの経験から,人生は取引と同じで,起伏があり,未知に満ちていることを学びました。私たちは常に,すでに起こった出来事から何かを学び,存在していないかもしれない真実にゆっくり近づくことを望んでいます。

雑談は少なく,正題に突入する。 取引が活発な株は通常,買入価格差が比較的小さいことを知っていますが,取引が活発でない株は,その逆です。 なぜこのような状況が起こるのでしょうか? 価格差の説明をシンプルで美しい数学モデルで説明できるでしょうか? 本日のEKOPモデル[初めは,異なる情報を持つトレーダーの行動が,この2種類の株式価格の差異の原因であるかどうかを研究するために提出された.このコラム記事では,このモデルの基礎を紹介する.モデルの適用については,後続記事で (もし私が時間があれば) 更に分析する.数学モデルの簡潔さは,この論文で示された美しさに尽き,論文を読む過程は楽しさに満ちている.

• #### 2 取引過程の仮定

金融モデルについて語るとき,最も重要なことは,そのモデルの仮定を注意することです.良い金融モデルには,それなりの仮定があります.それは,普遍性がないほど強くないし,美しい簡潔な結果を推論できないほど弱くないです.EKOPモデルの基本仮定は以下の通りです.

仮説1:我々は,株の取引について,取引の行動は日中に散発し,日中に連続した仮説を議論する.つまり,トレーダーの取引は,これらの散発した取引日の中で /upload/asset/8eeada05ae62fa9a4d5cf8f0acf05a5cc760c562.pngで発生する.そして,取引日の中で,取引は, /upload/asset/57926eb5a1e7fa14063c4148b25499190bfa6919.pngで,このような連続した時間に発生する.

• 悪いニュースは,株価は 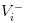と記入されています.
• 株価は 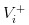と表記されています.
• 株価は 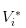と記入されています.

/upload/asset/6487043d156510fd43080526c4b2fef3850e99d4.pngが表示されています.

仮説2:ある日,α

株価に影響する事件が起こる確率は1−αで,株価に影響しない事件が起こる確率は1−αである.事件が起こる日には,株価を下げる悪い事件が起こる確率は1−δで,株価を上げる良い事件が起こる確率は1−δである.

仮説3:株式取引の参加者は,市場メーカー (MM),知られたトレーダー (IT),および知られていないトレーダー (UT) がある.彼らはそれぞれ以下の取引行動を遵守する.

MMは常に1ユニットの買取または販売のオートに掛ける準備ができていて,市場商人としての義務を果たしている.MMはリスク中立であるため,彼が掛けた価格は,彼が自分の考えでは公正な価格である.

ITはニュースが起こった日にのみ取引し,彼らの取引は休憩のプロセスである.ある日,悪いニュースが起こった場合,彼はμの到着率で売り切りを掛ける.そして,良いニュースが起こった日,彼はμの到着率で買い切りを掛ける.

UT (UT) は,私たちの哀れな菜です. メッセージの優位性がないので,彼らの取引は,毎日,到着率で,購入と販売の表を掛けるという,安らかなプロセスです. 注意してください,ここではすべてのポソンプロセスは相互に独立しています. 仮説3を図で示します.

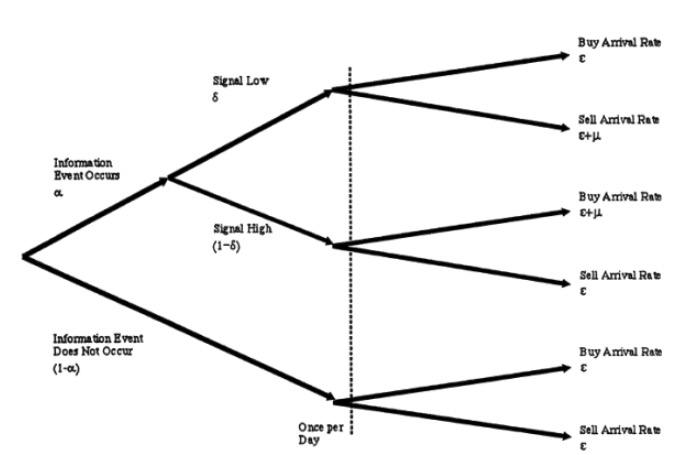
• #### 3 取引と価格の更新

市場商人というのは,大企業で働くのが常だと知っています。彼らは頭が良く,ITとUTとの長期の闘いの中で,膨大な歴史的データ分析によって,上記のツリーグラフのモデルパラメータをまとめています。しかし,幸いなことに,彼らは知的なトレーダーほど強くないのです.ある取引日が開かれる頃には,取引先のように,その日何か重要なことが起こったかどうかについて,胸に思いません。彼らができることは,その取引日の取引を進める過程で,他のトレーダーのレポートの行動を通して,その日の出来事,良いことなのか悪いことなのかを,常に更新することです。友好的な提醒:上記のすべてが仮定です。これは理解しやすいものです。特に,市場商人として,もし私が取引の過程で,この日の購入券が特別なものだと発見したならば,私は自然に,この日の購入券が特別なものだと推測します.そして,もし私がその日の取引を進めていると知的なトレーダーのように,その日の出来事が何か重要なものであったかどうかについて,胸に思いません。その日の取引を進める過程で,他のトレーダーのレポートの行動を通して,この日の出来事が良いものであったか悪いものであったかについて,自分自身に

では,MMの役を演じて ITとUTと戦ってみましょう. ある時点で,私たちは,何もないこと,良いこと,悪いことの確率のベクトルとして,

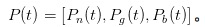┃ 明らかに,一日が始まったばかりの,つまり, 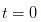のとき,私は,一枚のレシートを1つも見ていないので,私は,何も起こらない確率はαであり,良いことが起こる確率は /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.pngであり,悪いことが起こる確率は /upload/asset/87418f07b12fce65f4c3f70b24b0e94d2e19f769a.pngであると考えることができる.

さて,この確率はどうやって更新すべきでしょうか? 市場を分析する人はベイエスの公式を知っているでしょう. 売り切れが起きた場合,ベイエスの法則を使って,自分の確率を更新します. まず,今日のニュースがない確率を更新します.

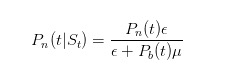
この式は,情報がないとき,無知のトレーダーだけがεで売る,という分子で,分母は,無知のトレーダーがいつでもεで売る,知のトレーダーが悪いことが起こったときだけμで売る,という分子で,同じように推論できます.

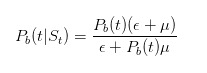
そして

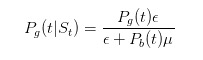
推論を続ける前に,ちょっとしたテストをしてみましょう. 売り札を見たら, 悪いことが起こる確率は 大きくなるはずです.

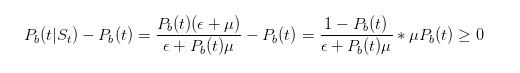
推論は直感を裏付けていることがわかります.

この確率を更新したら, 公正価格を計算して, 市場から購入する価格として,

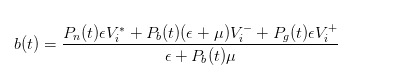
同じ推論で,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,買い手として,

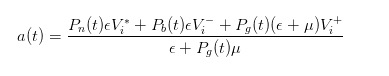
• #### 4 価格の変換後の価格差表現

上記の購入価格と販売価格の表現は直観的ではないので,単純化するために,t時点の株式の期待値を導入することができます.

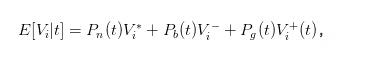
この式は,bidとaskの表記を,

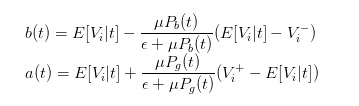
価格の差を明確に表すには,

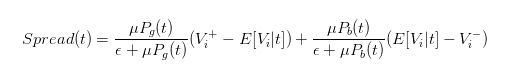
• #### 5 価格差に対するトレーダーの行動の影響

価格差の表記法があれば, 価格差に対する様々な取引者の影響を分析できます!

菜が多くなるほど,価格差は小さくなります。 注意して,εは知られていないトレーダー (菜と呼ぶことにしましょう) の到達率であり,もしε >> μがあれば,/upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.pngの両方が0に近づくことになるので,スプレッドも0に近づくことになる。 菜がないと取引はない。また別の極端に進むと,市場には菜がないと仮定し,菜よりも精巧な知識商のグループしかいないと仮定すると,悲惨な結果として,私たちが掲げる価格は 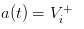と 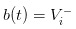となる.知識商は,購入と販売がどうであれ利益が見込めないことを発見し,市場は必ず沈んでいくだろう。。。

数学的なモデルの魅力とは,いくつかの仮定に基づいて,非常に単純な数学的な推論を用いて,このような興味深い,そして深い結論を導き出すことです. この記事を読んだ後,皆さんにも菜を親切に扱ってもらいたいと思います. 菜は,市場が正常な取引を行うための保証です!

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.