前回の記事では、暗号通貨市場における一般的な現象について検討しました。ほとんどの暗号通貨、特にビットコインやイーサリアムの価格変動に追随する暗号通貨は、上昇と下降が同時に起こる傾向を示すことが多いのです。この現象は、主流通貨との高い相関関係を明らかにしています。ただし、異なる暗号通貨間の相関の程度は異なります。では、この相関関係の違いは各通貨の市場パフォーマンスにどのように影響するのでしょうか?この記事では、2023 年後半の強気相場を例にこの問題を検討します。

暗号通貨市場の同期性のルーツ

暗号通貨市場は、その変動性と不確実性で知られています。ビットコインとイーサリアムは、市場の二大巨頭として、価格動向において主導的な役割を果たすことが多いです。市場競争力と取引活動を維持するために、ほとんどの小規模または新興のデジタル通貨は、これらの主流通貨、特にプロジェクト関係者が作成した通貨とある程度の価格同期を維持する傾向があります。この同期は市場参加者の心理的な期待と取引戦略を反映しており、定量的取引戦略の設計において重要な考慮事項となります。

相関式と計算方法

定量取引の分野では、相関関係の測定は統計的手法によって行われます。最も一般的に使用される指標はピアソン相関係数であり、これは 2 つの変数間の線形関連の度合いを測定します。以下に、いくつかの基本的な概念と計算方法を示します。

ピアソン相関係数 (r で表記) の範囲は -1 から +1 です。+1 は完全な正の相関、-1 は完全な負の相関、0 は線形相関がないことを示します。係数は次のように計算されます。

\(r = \frac{\sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n} (X_i - \bar{X})^2} \sqrt{\sum_{i=1}^{n} (Y_i - \bar{Y})^2}}\)

ここで、\(X_i\)と\(Y_i\)は2つのランダム変数の観測値であり、\(\bar{X}\)と\(\bar{Y}\)はそれぞれ2つのランダム変数の平均です。 Python の科学計算関連パッケージを使用すると、相関を計算するのに非常に便利です。

データ収集

この記事では、2023年通年のBinanceの4時間Kラインデータを収集し、1月1日に上場された144通貨を選択します。具体的なダウンロードデータコードは以下の通りです。

import requests
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

ticker = requests.get('https://fapi.binance.com/fapi/v1/ticker/24hr')
ticker = ticker.json()
sort_symbols = [k['symbol'][:-4] for k in sorted(ticker, key=lambda x :-float(x['quoteVolume'])) if k['symbol'][-4:] == 'USDT']

def GetKlines(symbol='BTCUSDT',start='2020-8-10',end='2023-8-10',period='1h',base='fapi',v = 'v1'):
    Klines = []
    start_time = int(time.mktime(datetime.strptime(start, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000
    end_time =  min(int(time.mktime(datetime.strptime(end, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000,time.time()*1000)
    intervel_map = {'m':60*1000,'h':60*60*1000,'d':24*60*60*1000}
    while start_time < end_time:
        time.sleep(0.5)
        mid_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        url = 'https://'+base+'.binance.com/'+base+'/'+v+'/klines?symbol=%s&interval=%s&startTime=%s&endTime=%s&limit=1000'%(symbol,period,start_time,mid_time)
        res = requests.get(url)
        res_list = res.json()
        if type(res_list) == list and len(res_list) > 0:
            start_time = res_list[-1][0]+int(period[:-1])*intervel_map[period[-1]]
            Klines += res_list
        if type(res_list) == list and len(res_list) == 0:
            start_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        if mid_time >= end_time:
            break
    df = pd.DataFrame(Klines,columns=['time','open','high','low','close','amount','end_time','volume','count','buy_amount','buy_volume','null']).astype('float')
    df.index = pd.to_datetime(df.time,unit='ms')
    return df

start_date = '2023-01-01'
end_date   = '2023-11-16'
period = '4h'
df_dict = {}

for symbol in sort_symbols:   
    print(symbol)
    df_s = GetKlines(symbol=symbol+'USDT',start=start_date,end=end_date,period=period)
    if not df_s.empty:
        df_dict[symbol] = df_s

df_close = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
for symbol in symbols:
    df_s = df_dict[symbol]
    df_close[symbol] = df_s.close
df_close = df_close.dropna(how='any',axis=1)

市場レビュー

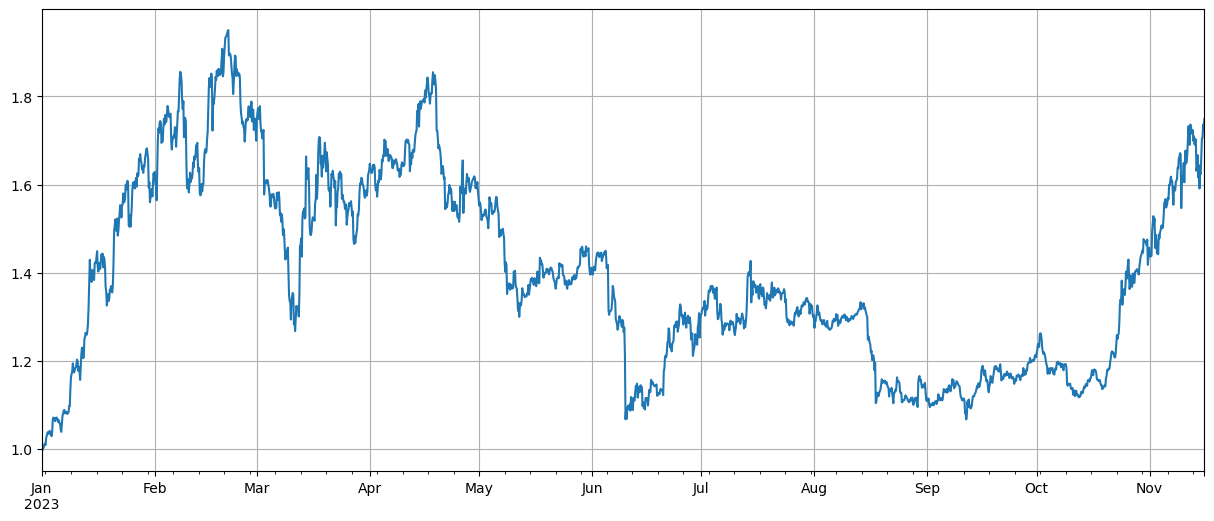
まず、データを正規化した後、平均価格上昇指数と下落指数を計算しました。2023年の市況には2つの波があり、1つは年初に大きな上昇があり、もう1つは10月から大きく上昇。指数の最高値。

df_norm = df_close/df_close.fillna(method='bfill').iloc[0] #归一化
total_index = df_norm.mean(axis=1)
total_index.plot(figsize=(15,6),grid=True);

相関分析

Pandasには相関計算が組み込まれています。BTC価格との相関は下の図の通りです。ほとんどの通貨は正の相関関係があり、BTC価格に追随しますが、一部の通貨は負の相関関係があります。デジタル通貨市場における異常事態とみなされる。

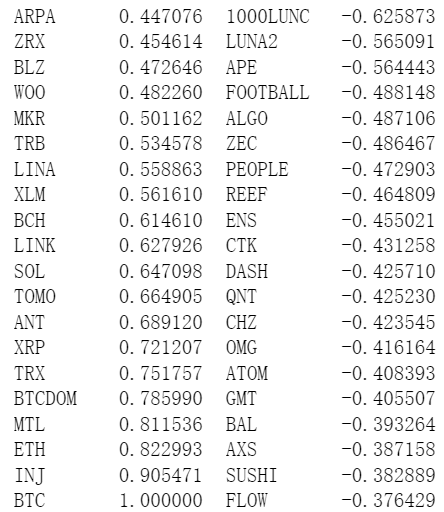
corr_symbols = df_norm.corrwith(df_norm.BTC).sort_values().index

相関関係と価格上昇

ここでは、通貨を大まかに2つのグループに分けます。最初のグループは、BTC価格と最も相関関係にある40通貨で構成され、2番目のグループは、BTC価格と最も相関関係のない通貨で構成されています。2つのグループのインデックスは、平均ロング第一グループに売りポジション、第二グループに売りポジションを置き、価格変動とBTCとの相関関係を計算できます。コードと結果は次のとおりです。

(df_norm[corr_symbols[-40:]].mean(axis=1)-df_norm[corr_symbols[:40]].mean(axis=1)).plot(figsize=(15,6),grid=True);

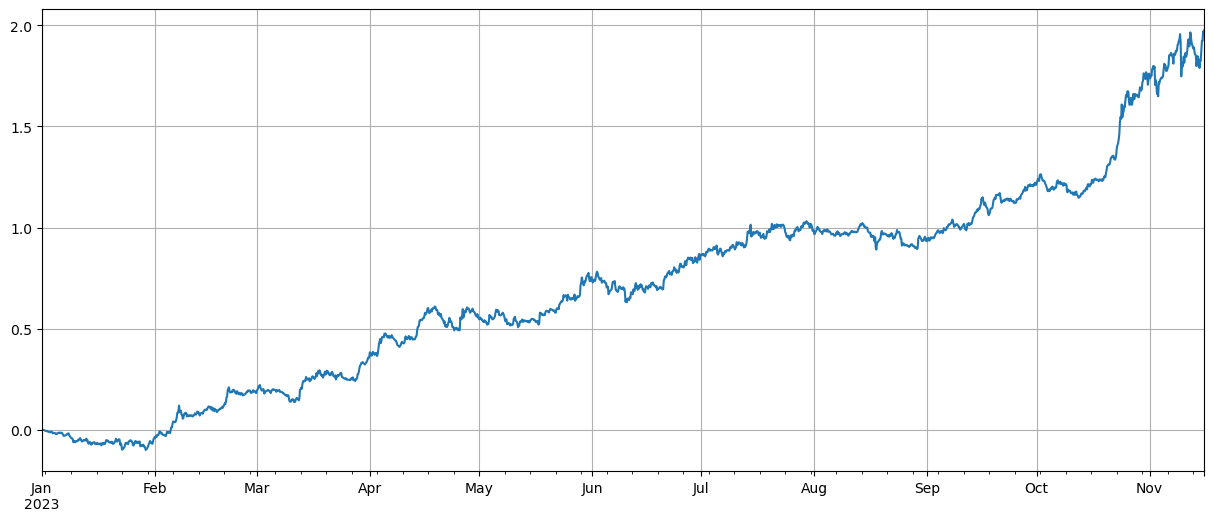
結果は、BTC 価格との相関が強い通貨の方が成長が良く、相関が低い通貨をショートすることも優れたヘッジの役割を果たすことを示しています。ここで不正確なのは、将来のデータが相関を計算するために使用されていることです。次に、データは2つのグループに分割され、1つは相関を計算するため、もう1つはヘッジ後のリターンを計算するためです。結果は下の図に示されています。結論は依然として同じです。

市場リーダーとして、ビットコインとイーサリアムの価格変動は市場全体に大きな影響を与えることが多いです。これらのビットコインの価格が上昇すると、通常、市場センチメントは楽観的になり、多くの投資家が市場のトレンドに従う傾向があります。投資家はこれを市場全体の上昇のシグナルと捉え、他の通貨を買い始めるかもしれない。主要通貨との相関性が高いコインは、市場参加者の集団行動により同様の価格上昇を経験する可能性があります。現時点では、価格動向に対する市場の予想は、自己達成的予言となることがあります。ビットコインと負の相関関係にある通貨は独特です。そのファンダメンタルズが悪化したか、もはや主流の投資家の目に留まらなくなった可能性があります。ビットコインの血を吸う市場さえあるかもしれません。市場はそれらを見捨てたのです。利益に追いつくことができるコインを追い求めます。

corr_symbols = (df_norm.iloc[:1500].corrwith(df_norm.BTC.iloc[:1500])-df_norm.iloc[:1500].corrwith(total_index[:1500])).sort_values().index 

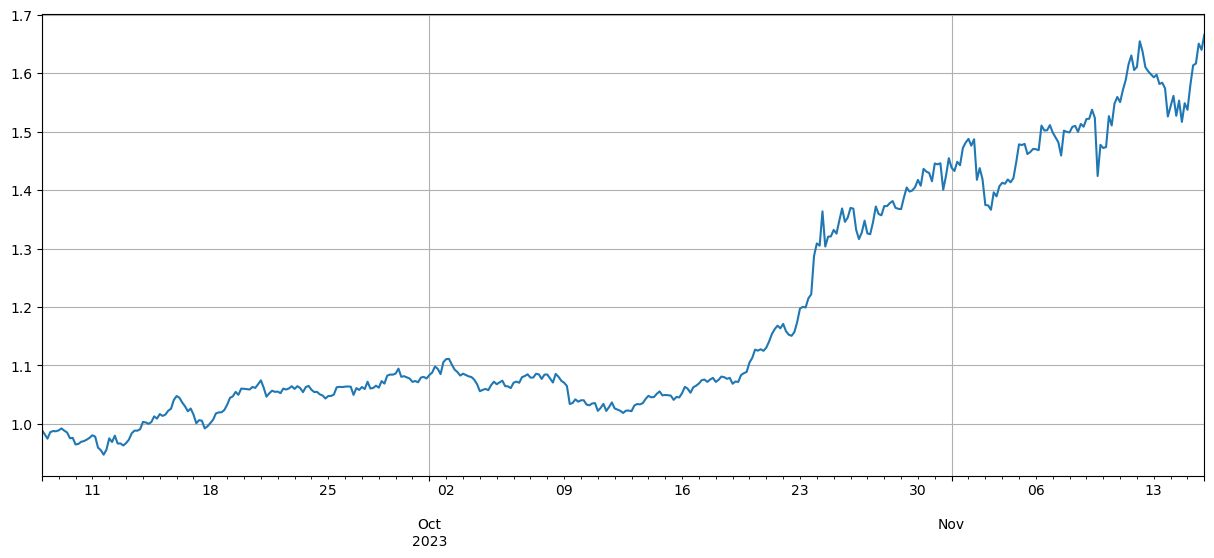
要約する

この記事では、ピアソン相関係数を使用して通貨間の相関の度合いを明らかにします。この記事では、通貨間の相関関係を計算するためのデータを取得し、そのデータを使用して市場の動向を評価する方法を説明します。デジタル通貨市場における価格変動の同期は、市場心理や戦略を反映しているだけでなく、科学的な手法によって定量化および予測できることが明らかになりました。これは、定量的な取引戦略の設計にとって特に重要です。

この記事のアイデアは、ローリング相関を計算したり、増加時と減少時の相関を個別に計算するなど、拡張できる領域が多数あり、より効果的な情報を分析できます。