SPYとIWM間の均等値回帰を利用した日中取引戦略

この記事では,日中取引戦略を書きます.これは,対回転対の古典的な取引理念を使用します.この例では,ニューヨーク証券取引所 (NYSE) で取引されている2つの取引型オープンインデックスファンド (ETF),SPY,IWMを利用し,米国株式市場指数であるS&P500とRussell 2000を代表しようとします.

この戦略は,複数のETFと別のETFを空にして利益差を生み出します. 多空間の比率は,統計的共調時間配列を用いた方法など,多くの方法で定義できます.このシナリオでは,ローリングラインナリー回帰によってSPYとIWMとの間のヘッジ比率を計算します.これは,SPYとIWMの間に利益差を生み出し,zスコアとして標準化します.zスコアが特定の値を超えると,取引信号が生じます.この利益差が平均値に戻ると信じているからです.

この戦略の基本原理は,SPYとIWMはほぼ同じ市場状況,つまり大小の米国企業の株価のパフォーマンスを代表するものである.前提は,価格の均等が回帰理論を受け入れた場合,それは常に回帰する時がある.事件は,S&P500とラッセル2000に非常に短い時間でそれぞれ影響を与える可能性があるため,しかし,それらの間での利回りの差は常に正常な平均に戻り,長期間の価格配列は常に統合されている.

戦略

この戦略は次のステップで実行されます:

データ - 2007年4月から2014年2月までの間,SPYとIWMの1分間のk線図が入手された.

処理 - データを正しくアレンジし,互いに欠けているk文字列を削除する.

差 - 2つのETF間のヘッジ比率は,回転線形回帰計算を用います. これは,回転窓を使用したβ回帰系数として定義され,この回転窓は1根k線を前に移動し,回帰系数を再計算します. したがって,ヘッジ比率βiは,根K線は,横断点をbi-1-kからbi-1に計算することによって,k線を回転するために使用されます.

Z-Score - 標準利差の値は通常の方法で計算される.これは利差の平均値 (サンプル) を減算して利差の標準差 (サンプル) を除算することを意味します.これは,Z-Scoreが次元のない量であるため,値参数を理解しやすくするためです.

取引 - 負のzスコア値が設定された (または後最適化) 限界値を下回ると多発信号が発生し,空発信号は逆である. zスコア値の絶対値が追加的な限界値を下回ると平衡信号が発生する. この戦略のために,私は (少しランダムに) 引き上げz = 2を開場値と引き上げz = 1を平衡値として選択した. 均等値回帰が利差に作用すると仮定すると,上記のものは,この利息関係を捕捉して良い利益をもたらすことを期待する.

戦略を深く理解する最良の方法は,実際に実行することです. 次のセクションでは,この均等値帰帰策を実行するための完全なPythonコード (単一のファイル) が詳細に説明されています. 詳細なコード注釈を追加して,よりよく理解できるようにしました.

Pythonの実装

すべてのPython/pandasチュートリアルと同様に,このチュートリアルで説明するPython環境に従って設定する必要があります. 設定が完了すると,最初のタスクは必要なPythonライブラリをインポートすることです. これはmatplotlibとpandasを使用するには必須です.

ウェブのデータベースは,ウェブのデータベースとリンクされています.

パイソン - 2.7.3 NumPy - 1.8.0 パンダ 0.12.0 マットプロットリブ - 1.1.0

データベースの詳細はこちらです.

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

次の関数 create_pairs_dataframeは,二つのシンボルを含む内部のk線のCSVファイルを2つ輸入します.この例では,SPYとIWMになります.その後,単一のデータペアペアを作成します.このデータペアペアは,二つの原始ファイルのインデックスを使用します.逃した取引やエラーにより,それらのタイムフレームが異なる可能性があります.これはpandasのようなデータベースを使用する主な利点の1つです.私たちは非常に効率的な方法でサンプルコードをします.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

次のステップは,SPYとIWMの間にローリングラインナリー回帰を行う.このシナリオでは,IWMは予測器 (x),SPYは応答器 (y) である.私は100根のk線をデフォルト回帰ウィンドウに設定している.上記のように,これは方針のパラメータである.方針が堅牢であると考えられるために,理想的には,回帰レポートが回帰期間に凸関数状態 (x) または他の性能メタルの表現を示すことを望む.したがって,コードの後期には,変化範囲内の回帰期を通して敏感性分析を行う.

SPY-IWMの線形回帰モデルで,beta系数を計算し,DataFrameに追加し空行を削除した. これで最初のK線が構築され,回帰長さの切削メタファーに等しい. その後,SPYの単位とIWMの-βiの単位で2つのETFの利息差を作成した.明らかに,これは現実的ではありません.

最後に,利息の平均値を減算して標準利息の標準利息を計算する利息差のzスコアを作成します. ここで注意すべきは,かなり微妙な先見偏差が存在していることです. 私は意図的にそれをコードに留めたので,研究でそのような間違いを犯すのがどれほど容易かを強調したいです. 利息時間配列全体の平均値と標準利差を計算します. もしそれが真の歴史的精度を反映しようとすると,これらの情報は得られないでしょう. それは暗黙的に将来の情報を利用しているからです. したがって,私たちはローリング平均値とdevst値を使用してzスコアを計算する必要があります.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

create_long_short_market_signalsでは,取引信号を作成します.これらは,zスコアの値が値を超えると計算されます. zスコアの絶対値が他の (より小規模な) 値よりも小さいとき,平衡信号が与えられます.

この状態を実現するために,k線ごとに開いた仓庫か平らな仓庫を設定する取引戦略を確立することが必要である. long_marketと short_marketは,多頭と空頭の位置を追跡するために定義された2つの変数である.残念ながら,ベクトル化方法と比較して,イリテラルな方法でプログラミングすることがより簡単であり,したがって計算は遅い. 1分間のk線図のCSVファイルごとに約700,000のデータポイントが必要であるにもかかわらず,私の古いデスクトップでは計算は比較的速い!

パンダスの DataFrame をイリテージするには (これは間違いなく珍しい操作です) iterrows 方法を使用する必要があります.

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

この段階では,ペアを更新し,実際の多,空のシグナルを含めるようにしました.これは,私たちがポジションを開く必要があるかどうかを判断できるようにしました.今,ポジションの市場価値を追跡するポートフォリオを作成する必要があります.最初の課題は,多頭シグナルと空頭シグナルを組み合わせた位置列を作成することです.これは,1から1までの要素を列に含みます.,1は多頭シグナルを表し,0は空頭シグナルを代表します.

ETFの市場価値が作成されたら,k行の終わりに合計市場価値を生成するためにそれらを組み合わせます.その後,そのオブジェクトのpct_change方法によってそれを返還値に変換します.次のコード行では誤ったエントリ (NaNとinf要素) を削除し,最後に完全な利害曲線を計算します.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

主関数はそれらを結合します. 日中のCSVファイルはdatadirのパスにあります. あなたの特定のディレクトリを指すように以下のコードを変更してください.

策略がlookback周期にどの程度敏感かを決定するために,lookbackのパフォーマンス指標を数える必要がある.私はポートフォリオの最終総返済パーセントをパフォーマンス指標とlookback範囲[50,200]として選択し,10のインクリメントで示した.以下のコードでは,前の関数はこの範囲内のforループに含まれ,他の限界値は変わらないことがわかります.

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

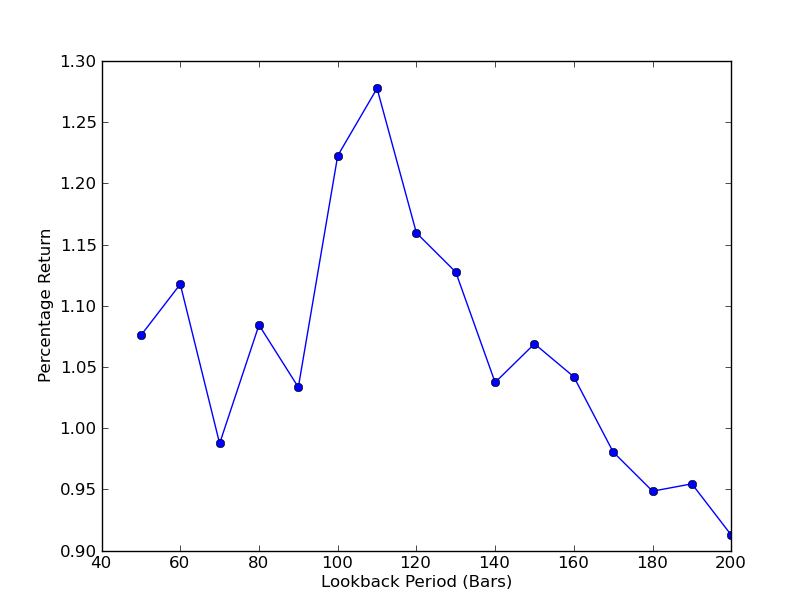
lookbacks と returns のグラフが表示される. lookback は,全局的なの最大値である 110 基k 線を持つ. lookbacks と returns の関係がないことが示されている場合,それは:

SPY-IWM線性回帰ヘッジ比lookback期間の敏感性分析

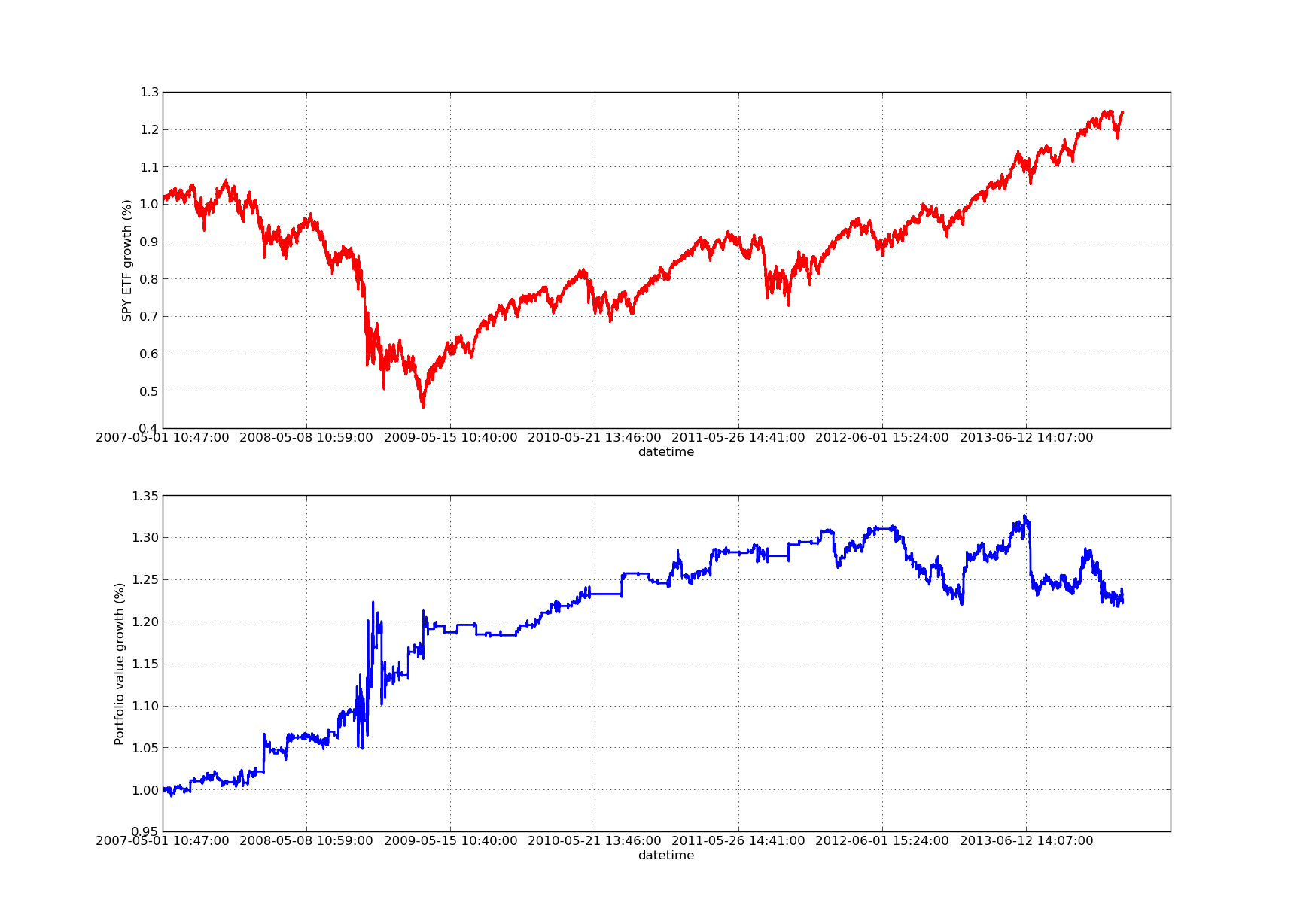
向上傾斜の利回り曲線がないと,どんなリトーク記事も不完全です!したがって,累積利回りと時間との曲線を描きたい場合は,次のコードを使用できます.それはlookbackパラメータの研究から生成される最終投資ポートフォリオを描きます.したがって,あなたが視覚化したいグラフに基づいてlookbackを選択することが必要です.このグラフは,比較を助けるために同期SPYの返還も描いています:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

フォローしている権利・利益曲線グラフの Lookback Period は 100 日です.

SPY-IWM線性回帰ヘッジ比lookback期間の敏感性分析

金融危機の間,2009年のSPYは大きく縮小した.この戦略は,この時期も不安定な時期にあった.また,SPYが,この期間における強い傾向性によって,スタンダード500指数を反映したため,昨年の業績が悪化したことも注意してください.

注目すべきは,zスコアの利差を計算する際に,我々は依然として前向きな偏差を考慮する必要がある.さらに,これらの計算はすべて取引コストがない状態で行われている.これらの要因を考慮すると,この戦略は確実に悪い結果をもたらす.手続費とスライドポイントは,現在決定されていません.また,この戦略は,ETFの小数単位で取引されているので,これは非常に非現実的です.

以降の記事では,より複雑なイベント駆動バックテストを作成し,上記の要素を考慮し,資金曲線とパフォーマンス指標により自信を示します.