データ駆動型テクノロジーに基づくペア取引
 2
2
 2768
2768

ペア取引は、数学的分析に基づいて取引戦略を開発する優れた例です。この記事では、データを活用してペア取引戦略を作成し、自動化する方法を説明します。
基本原則
ペプシとコカコーラのように、両方の会社が同じ製品を生産しているなど、何らかの根本的な相関関係がある投資 X と Y のペアがあるとします。 2 つの価格比率または基準 (スプレッドとも呼ばれる) が時間の経過とともに一定に保たれるようにします。ただし、投資対象に対する大量の売買注文や、いずれかの企業に関する重要なニュースへの反応など、一時的な需給の変化により、2 つの通貨ペア間のスプレッドが時々乖離する場合があります。この場合、一方の投資は相対的に上昇し、もう一方の投資は相対的に下降します。この乖離が時間の経過とともに正常化すると予想される場合は、取引の機会 (または裁定取引の機会) を見つけることができます。このような裁定取引の機会は、BTC と安全資産の関係、先物における大豆粕、大豆油、大豆品種の関係など、デジタル通貨市場や国内商品先物市場のいたるところにあります。
一時的な価格差がある場合、トレードではパフォーマンスの良い投資(上昇した投資)を売り、パフォーマンスの悪い投資(下落した投資)を買います。2つの投資の間には違いがあることは間違いありません。スプレッドは、最終的には、パフォーマンスのよい投資が下落するか、パフォーマンスの悪い投資が上昇するか、またはその両方として反映されます。これらのすべてのシナリオで、取引は利益を生みます。投資額が両者の差額を変えずに同時に上がったり下がったりした場合、利益も損失も出ません。
したがって、ペア取引は、上昇トレンド、下降トレンド、横ばいなど、ほぼすべての市場状況からトレーダーが利益を得ることができる市場中立の取引戦略です。
概念を説明する: 2つの仮想投資ターゲット
- Inventor Quantitative Platform 上での研究環境の構築
まず、スムーズに作業を進めるためには、研究環境を構築する必要があります。この記事では、主に便利で高速なAPIを使用できるように、Inventor Quantitative Platform(FMZ.COM)を使用して研究環境を構築します。このプラットフォームのインターフェースとカプセル化は後で行います。完全な Docker システム。
Inventor Quantitative Platform の正式名称では、この Docker システムはホスト システムと呼ばれます。
ホストとロボットの展開方法の詳細については、以前の記事を参照してください: https://www.fmz.com/bbs-topic/4140
独自のクラウド コンピューティング サーバー展開ホストを購入したい読者は、この記事を参照してください: https://www.fmz.com/bbs-topic/2848
クラウドコンピューティングサービスとホストシステムを正常に展開したら、最も強力なPythonツールであるAnacondaをインストールします。
この記事で必要なすべての関連プログラム環境 (依存ライブラリ、バージョン管理など) を実現するには、Anaconda を使用するのが最も簡単な方法です。これは、パッケージ化された Python データ サイエンス エコシステムおよび依存関係マネージャーです。
Anacondaのインストール方法については、Anacondaの公式ガイドを参照してください:https://www.anaconda.com/distribution/
この記事では、Python 科学計算で非常に人気があり重要な 2 つのライブラリである numpy と pandas も使用します。
上記の基本的な作業については、Anaconda環境とnumpyとpandasの2つのライブラリの設定方法を説明した前回の記事も参照してください。詳細については、https://www.fmz.com/digest-をご覧ください。トピック/4169
次に、コードを使用して「2つの仮想投資ターゲット」を実装してみましょう。
import numpy as np
import pandas as pd
import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)
import matplotlib.pyplot as plt
はい、Python の非常に有名なチャートライブラリである matplotlib も使用します。
仮想投資資産 X を生成し、正規分布を使用してその日次収益をプロットするシミュレーションを行ってみましょう。次に累積合計を実行して毎日の X 値を取得します。
# Generate daily returns
Xreturns = np.random.normal(0, 1, 100)
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
Xreturns), name='X')
+ 50
X.plot(figsize=(15,7))
plt.show()
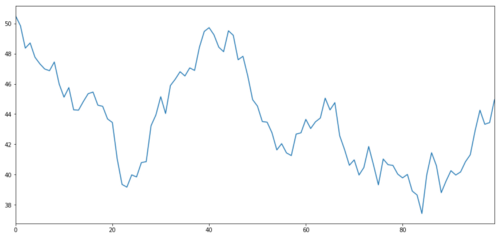
投資対象Xの毎日の収益を正規分布でシミュレートして描画する
ここで、X と強く相関する Y を生成すると、Y の価格は X の変化と非常によく似た動きをするはずです。これをモデル化するには、X を取得して上方にシフトし、正規分布から抽出したランダム ノイズを追加します。
noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()
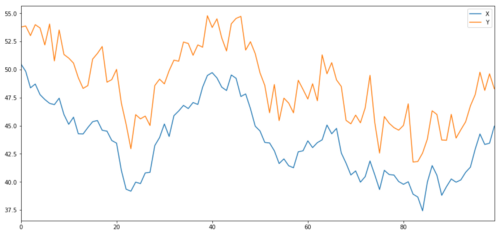
共和投資対象XとY
共和分
共和分は相関関係と非常によく似ており、2 つのデータ系列間の比率が平均を中心に変化することを意味します。2 つの系列 Y と X は次のようになります。
Y = ⍺ X + e
ここで、⍺ は定数比、e はノイズです。
2 つの時系列間の取引ペアの場合、時間の経過に伴う比率の期待値は平均に収束する必要があります。つまり、それらは共和分される必要があります。上記で構築した時系列は共和分化されています。次に、2 つの間のスケールを描いて、どのように見えるかを確認します。
(Y/X).plot(figsize=(15,7))
plt.axhline((Y/X).mean(), color='red', linestyle='--')
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()
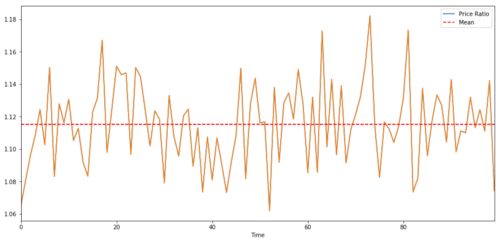
2つの共和分投資の価格の比率と平均
共和分検定
これをテストする便利な方法は、statsmodels.tsa.stattools を使用することです。可能な限り共和分化された 2 つのデータ シリーズを人工的に作成したため、p 値は非常に低くなるはずです。
# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue
結果は1.81864477307e-17です。
注: 相関と共和分
相関と共和分は理論的には似ていますが、同じではありません。相関しているが共和分化していないデータ系列の例、およびその逆の例を見てみましょう。まず、生成したばかりの系列の相関関係を確認しましょう。
X.corr(Y)
結果は0.951です
予想通り、これは非常に高いです。しかし、相関はあっても共和分ではない 2 つの系列の場合はどうなるでしょうか?簡単な例としては、異なる 2 つのデータ シリーズが挙げられます。
ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)
s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')
pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)
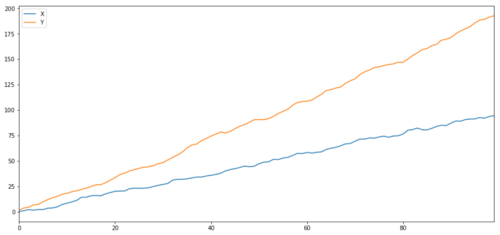
2 つの関連シリーズ (相互統合されていない)
相関係数: 0.998 共和分検定 p値: 0.258
相関関係のない共和分の簡単な例としては、正規分布する系列と方形波があります。
Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)
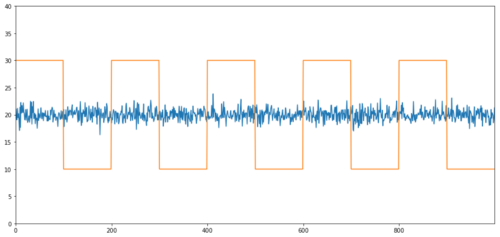
相関: 0.007546 共和分検定 p値: 0.0
相関は非常に低いですが、p 値は完全な共和分を示しています。
ペア取引を行うにはどうすればいいですか?
2 つの共和分時系列 (上記の X と Y など) は互いに近づいたり離れたりするため、高い基準値と低い基準値が存在する場合があります。 1 つの投資を購入し、別の投資を売却することでペア取引を実行します。このように、2 つの投資対象が同時に下落または上昇した場合、利益も損失も発生せず、つまり市場中立になります。
上記のY = ⍺ X + eのXとYに戻ると、比率(Y/X)をその平均⍺の周りで動かすことで利益を得ることができます。これを行うには、Xが⍺の値が大きすぎると、高すぎるか低すぎる場合、⍺の値が高すぎるか低すぎます。
ロング比率: これは比率⍺が小さく、大きくなると予想される場合です。上記の例では、Y をロング、X をショートしてポジションを開きます。
ショート レシオ: これは、比率 ⍺ が大きく、小さくなることが予想される場合です。上記の例では、Y をショートし、X を買いポジションを開きます。
我々は常に「ヘッジされたポジション」を持っていることに注意してください。つまり、原資産のロングが価値を失えば、ショート ポジションは利益を上げ、その逆もまた同様であるため、市場全体の動きの影響を受けません。
資産 X と Y が相互に相対的に動くと、利益が出たり損失が出たりします。
データを使用して同様の行動をとる取引を見つける
これを行う最善の方法は、共和分である可能性があると疑われる取引から始めて、統計テストを実行することです。すべての取引ペアに対して統計テストを実行すると、多重比較バイアスの被害者。
多重比較バイアス多数のテストを実行する必要があるため、多くのテストを実行すると、有意な p 値が誤って生成される可能性が高くなる状況を指します。このテストをランダム データで 100 回実行すると、0.05 未満の p 値が 5 つ表示されるはずです。共和分について n 個の機器を比較する場合、n(n-1)/2 の比較を実行することになり、多くの不正確な p 値が表示されます。これは、テスト サンプル サイズが大きくなるにつれて増加します。そして、増加します。これを回避するには、共和分である可能性が高いと考えられるいくつかの取引ペアを選択し、個別にテストします。これにより、多重比較バイアス。
それでは、共和分を示す金融商品をいくつか見つけてみましょう。S&P 500 の米国大手テクノロジー株のバスケットを見てみましょう。これらの金融商品は同様の市場セグメントで運用されており、共和分を示しています。価格。取引商品のリストをスキャンし、すべてのペア間の共和分をテストします。
返された共和分テスト スコア マトリックス、p 値マトリックス、および p 値が 0.05 未満のすべてのペアワイズ マッチが含まれます。この方法は多重比較バイアスが発生しやすいため、実際には 2 回目の検証を実行する必要があります。 この記事では、説明の便宜上、例ではこれを無視することにします。
def find_cointegrated_pairs(data):
n = data.shape[1]
score_matrix = np.zeros((n, n))
pvalue_matrix = np.ones((n, n))
keys = data.keys()
pairs = []
for i in range(n):
for j in range(i+1, n):
S1 = data[keys[i]]
S2 = data[keys[j]]
result = coint(S1, S2)
score = result[0]
pvalue = result[1]
score_matrix[i, j] = score
pvalue_matrix[i, j] = pvalue
if pvalue < 0.02:
pairs.append((keys[i], keys[j]))
return score_matrix, pvalue_matrix, pairs
注: データには市場ベンチマーク (SPX) が含まれています。市場は多くの金融商品のフローを駆動し、共和分化しているように見える2つの金融商品が見つかることがありますが、実際には相互に共和分化しているわけではなく、市場。これは交絡変数と呼ばれます。見つかった関係性において市場参加を調べることが重要です。
from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
dataSetId=dataSetId,
instrumentIds=instrumentIds,
startDateStr=startDateStr,
endDateStr=endDateStr,
event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

それでは、私たちの方法を使用して、共和分取引ペアを見つけてみましょう。
# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds,
yticklabels=instrumentIds, cmap=’RdYlGn_r’,
mask = (pvalues >= 0.98))
plt.show()
print pairs
[('ADBE', 'MSFT')]
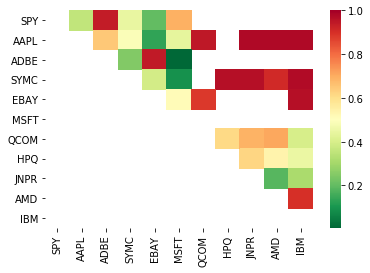
「ADBE」と「MSFT」は共和分化しているようです。実際に妥当かどうか確かめるために価格を見てみましょう。
S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()
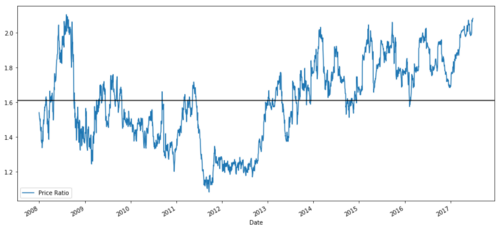
2008年から2017年までのMSFTとADBEの価格比率のグラフ
この比率は確かに安定した平均のように見えます。絶対比率は統計的にはあまり役に立ちません。信号を Z スコアとして表示して正規化すると、より役立ちます。 Z スコアは次のように定義されます。
Z Score (Value) = (Value — Mean) / Standard Deviation
警告する
実際には、データが正規分布している場合に限り、データに何らかの拡張を適用しようとします。ただし、多くの財務データは正規分布していないため、統計を生成する際には正規分布や特定の分布を単純に想定しないように十分注意する必要があります。比率の実際の分布には太い裾野がある可能性があり、極端に傾向するデータはモデルを混乱させ、大きな損失につながる可能性があります。
def zscore(series):
return (series - series.mean()) / np.std(series)
zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()
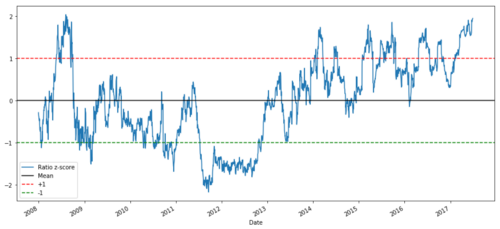
2008年から2017年までのMSFTとADBEのZ価格比率
これで、比率が平均値の周りでどのように動くかがわかりやすくなりましたが、平均値から大きく逸脱する傾向にある場合もあり、これを活用することができます。
ペア取引戦略の基本について説明し、価格履歴に基づいて共和分ターゲットを特定したので、取引シグナルを開発してみましょう。まず、データ技術を使用して取引シグナルを開発する手順を確認しましょう。
信頼できるデータの収集とデータのクリーニング
データから関数を作成し、取引シグナル/ロジックを識別する
特徴としては、移動平均や価格データ、より複雑な信号の相関関係や比率などが挙げられ、これらを組み合わせて新しい特徴を作成することができます。
これらの機能を使用して、買い、売り、ショートポジションのシグナルを生成します。
幸いなことに、Inventor Quantitative Platform (fmz.com) が上記の 4 つの側面を補完してくれます。これは戦略開発者にとって大きな恵みです。私たちは戦略ロジック、設計、機能拡張にエネルギーと時間を費やすことができます。
Inventor Quantitative Platform には、さまざまな主流の取引所のインターフェースがパッケージ化されています。必要なのは、これらの API インターフェースを呼び出すことだけです。残りの基礎となる実装ロジックは、専門チームによって洗練されています。
論理的な完全性と原理の説明のために、これらの基礎となるロジックを詳細に紹介しますが、実際の操作では、読者は Inventor Quant の API インターフェイスを直接呼び出して、上記の 4 つの側面を完了することができます。
始めましょう:
ステップ1: 問題を設定する
ここでは、次の瞬間に比率が買いになるか売りになるかを示すシグナル、つまり予測変数 Y を作成しようとしています。
Y = Ratio is buy (1) or sell (-1)
Y(t)= Sign(Ratio(t+1) — Ratio(t))
原資産の実際の価格や比率の実際の値を予測する必要はなく (予測することは可能ですが)、次に比率の方向を予測するだけでよいことに注意してください。
ステップ2: 信頼性が高く正確なデータを収集する
Inventor Quant はあなたの友達です!取引したい銘柄と使用したいデータ ソースを指定するだけで、必要なデータが抽出され、配当と銘柄の分割用にクリーンアップされます。したがって、ここにあるデータはすでに非常にクリーンです。
過去10年間の取引日について、Yahoo Financeの以下のデータ(約2,500データポイント)を使用しました:始値、終値、高値、安値、出来高
ステップ3: データを分割する
モデルの精度をテストするというこの非常に重要なステップを忘れないでください。私たちは以下のトレーニング/検証/テストの分割データを使用しています
Training 7 years ~ 70%
Test ~ 3 years 30%
ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]
理想的には、検証セットも作成しますが、現時点ではそうしません。
ステップ4: 特徴エンジニアリング
関連する機能は何でしょうか?比率の変化の方向を予測したい。 2 つの金融商品は共和分化しているため、この比率はシフトして平均値に戻る傾向があることがわかりました。私たちの特徴は、比率の平均の何らかの尺度であるべきであり、現在の値と平均の差によって取引シグナルを生成できると思われます。
以下の関数を使用します。
60日移動平均比率:移動平均の尺度
5日移動平均比率: 平均の現在の値の尺度
60日標準偏差
Z スコア: (5 日 MA - 60 日 MA) / 60 日 SD
ratios_mavg5 = train.rolling(window=5,
center=False).mean()
ratios_mavg60 = train.rolling(window=60,
center=False).mean()
std_60 = train.rolling(window=60,
center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()
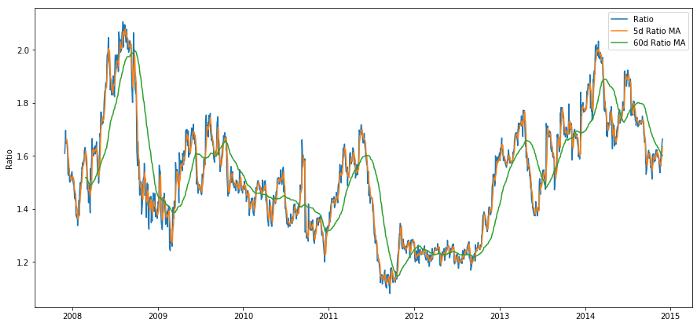
60日移動平均と5日移動平均の価格比率
plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()
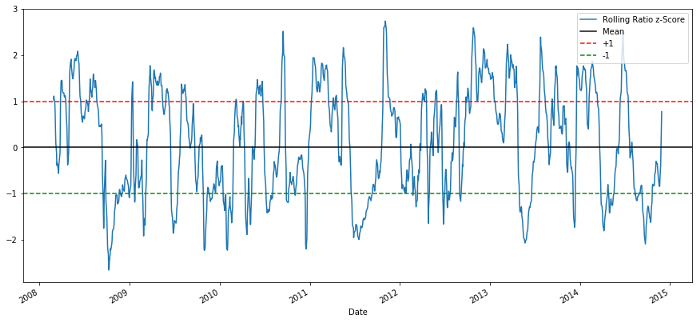
60-5 Zスコア価格比率
ローリング平均の Z スコアは、比率の平均回帰特性を実際に引き出します。
ステップ5: モデルの選択
非常に単純なモデルから始めましょう。 Z スコア グラフを見ると、Z スコアが高すぎる場合や低すぎる場合は必ず回帰することがわかります。高すぎる値と低すぎる値を定義するしきい値として +1/-1 を使用し、次のモデルを使用して取引シグナルを生成できます。
zが-1.0以下の場合、比率は買い(1)となる。なぜならzが0に戻ると予想されるため、比率は増加するからである。
zが1.0を超える場合、比率は売り(-1)です。これは、zが0に戻ると予想され、比率が下がるためです。
ステップ6: トレーニング、検証、最適化
最後に、モデルが実際のデータにどのような影響を与えるかを見てみましょう。この信号が実際の比率でどのように動作するかを見てみましょう
# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()
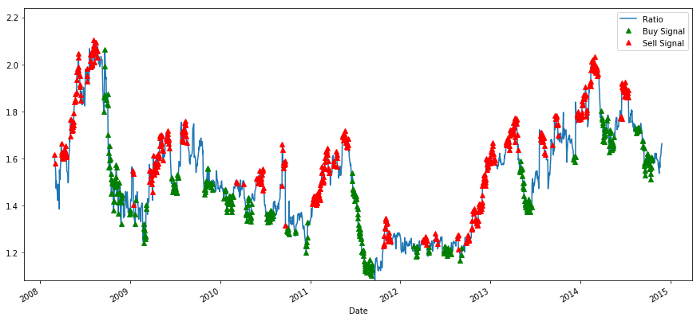
売買価格比率シグナル
このシグナルは妥当と思われます。比率が高いか増加しているとき(赤い点)に売り、比率が低いか減少しているとき(緑の点)に買い戻すようです。これは、私たちの取引の実際の主題にとって何を意味するのでしょうか?見てみましょう
# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()
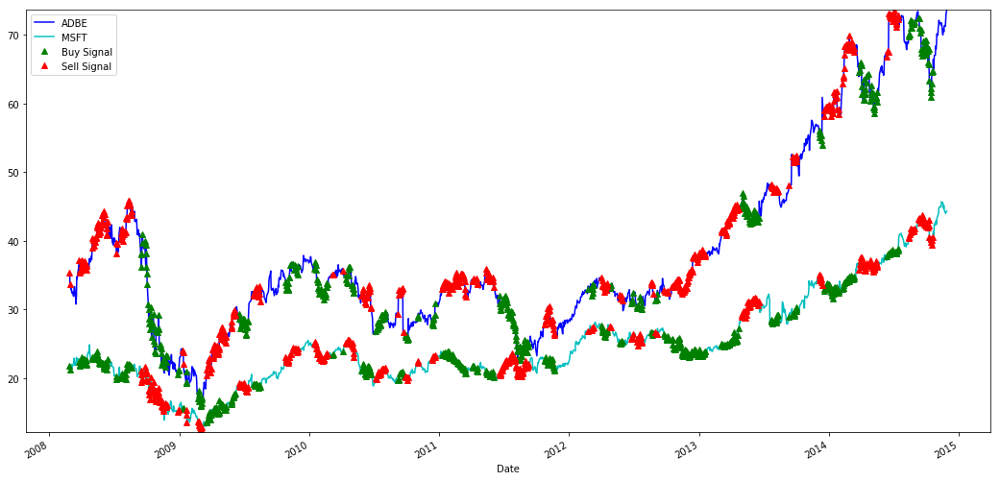
MSFT と ADBE 株の売買シグナル
時には「ショート レッグ」で利益を上げたり、「ロング レッグ」で利益を上げたり、その両方で利益を上げたりすることがあることに注目してください。
トレーニング データの信号に満足しています。このシグナルがどのような利益を生み出すか見てみましょう。比率が低いときに1比率(ADBE株1株を購入し、比率x MSFT株を売却)を購入し、1比率(ADBE株1株を売却し、コール比率x MSFT株を売却)を売却する簡単なバックテスターを作成し、これらの取引のPnLを計算できます。比率。
# Trade using a simple strategy
def trade(S1, S2, window1, window2):
# If window length is 0, algorithm doesn't make sense, so exit
if (window1 == 0) or (window2 == 0):
return 0
# Compute rolling mean and rolling standard deviation
ratios = S1/S2
ma1 = ratios.rolling(window=window1,
center=False).mean()
ma2 = ratios.rolling(window=window2,
center=False).mean()
std = ratios.rolling(window=window2,
center=False).std()
zscore = (ma1 - ma2)/std
# Simulate trading
# Start with no money and no positions
money = 0
countS1 = 0
countS2 = 0
for i in range(len(ratios)):
# Sell short if the z-score is > 1
if zscore[i] > 1:
money += S1[i] - S2[i] * ratios[i]
countS1 -= 1
countS2 += ratios[i]
print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
# Buy long if the z-score is < 1
elif zscore[i] < -1:
money -= S1[i] - S2[i] * ratios[i]
countS1 += 1
countS2 -= ratios[i]
print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
# Clear positions if the z-score between -.5 and .5
elif abs(zscore[i]) < 0.75:
money += S1[i] * countS1 + S2[i] * countS2
countS1 = 0
countS2 = 0
print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)
結果は1783.375です
つまり、この戦略は利益をもたらすようです!ここで、移動平均の時間ウィンドウを変更したり、買い/売りやポジションのクローズのしきい値を変更したりすることでさらに最適化し、検証データのパフォーマンスの向上を確認できます。
1/-1 予測には、ロジスティック回帰、SVM などのより複雑なモデルを試すこともできます。
さて、このモデルをさらに進めて、
ステップ7: テストデータをバックテストする
ここで、Inventor Quantitative Platformについて触れておきたいと思います。このプラットフォームは、高性能のQPS/TPSバックテストエンジンを使用して、過去の環境を忠実に再現し、一般的な定量的バックテストの罠を排除し、戦略の欠点を迅速に発見し、よりリアルな情報を提供します。 -時間の投資。助けを提供してください。
原理を説明するために、この記事では基礎となるロジックを示すことにしました。実際の応用では、読者はInventor Quantitative Platformを使用することをお勧めします。時間の節約に加えて、フォールトトレランス率を向上させることが重要です。
バックテストは簡単です。上記の関数を使用して、テストデータの PnL を表示できます。
trade(data[‘ADBE’].iloc[1762:], data[‘MSFT’].iloc[1762:], 60, 5)
結果は5262.868です
このモデルは非常によくできています!これは私たちの最初のシンプルなペア取引モデルとなりました。
過剰適合を避ける
最後に、オーバーフィッティングについて具体的にお話ししたいと思います。過剰適合は、取引戦略における最も危険な落とし穴です。オーバーフィッティング アルゴリズムは、バックテストでは非常に優れたパフォーマンスを発揮しますが、新しい未知のデータでは失敗する可能性があります。つまり、データの傾向を実際に明らかにすることはなく、実際の予測力はありません。簡単な例を見てみましょう。
私たちのモデルでは、ローリングパラメータ推定値を使用し、時間ウィンドウの長さを最適化することを目指しています。すべての可能性、妥当な時間ウィンドウの長さを単純に反復し、モデルが最適に機能する時間の長さを選択するという判断になるかもしれません。以下では、トレーニング データの PNL に基づいて時間ウィンドウの長さをスコアリングし、最適なループを見つけるための簡単なループを記述します。
# Find the window length 0-254
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762],
data['MSFT'].iloc[:1762], l, 5)
for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)
('Best window length:', 40)
ここで、テスト データでモデルのパフォーマンスをチェックすると、この時間ウィンドウの長さが最適からは程遠いことがわかります。これは、当初の選択がサンプル データに明らかに過剰適合しているためです。
# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:],
data['MSFT'].iloc[1762:],l,5)
for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset,
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])
(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)
明らかに、サンプル データでうまく機能するものが、将来的に必ずしも良い結果を生み出すとは限りません。テストのために、2つのデータセットから計算された長さスコアをプロットしてみましょう。
plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()
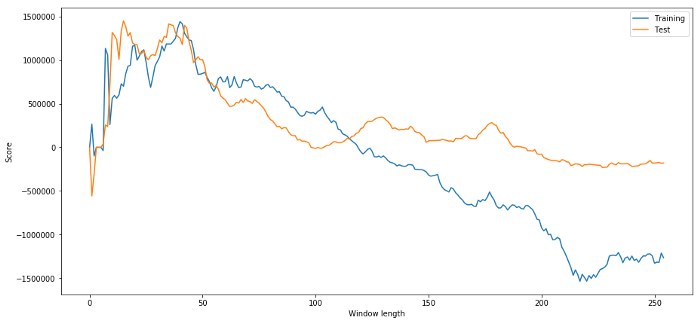
時間枠としては 20 ~ 50 が適切な選択であることがわかります。
過剰適合を回避するために、経済的推論またはアルゴリズムの特性を使用して時間ウィンドウの長さを選択できます。長さを指定する必要のないカルマン フィルターを使用することもできます。この方法については、後ほど別の記事で説明します。
次のステップ
この記事では、取引戦略を開発するプロセスを示すいくつかの簡単な入門方法を紹介します。実際には、より洗練された統計を使用する必要があり、次のオプションを検討できます。
ハースト指数
オルンシュタイン・ウーレンベック過程から推定される平均回帰の半減期
カルマンフィルタ