기계 학습에 기반한 주문서 고주파 거래 전략

기계 학습에 기반한 주문서 고주파 거래 전략

• 제1차 시론

  증권 시장의 거래 메커니즘은 제안운동 시장과 주문운동 시장으로 나눌 수 있다. 전자는 시장을 통해 유동성을 제공하는데 의존하고 후자는 제한 가격 문서를 통해 유동성을 제공하며 거래는 투자자의 구매 위탁과 판매 위탁 경매로 형성된다. 중국의 증권 시장은 주문운동 시장으로, 주식 시장과 선물 시장이 포함된다.

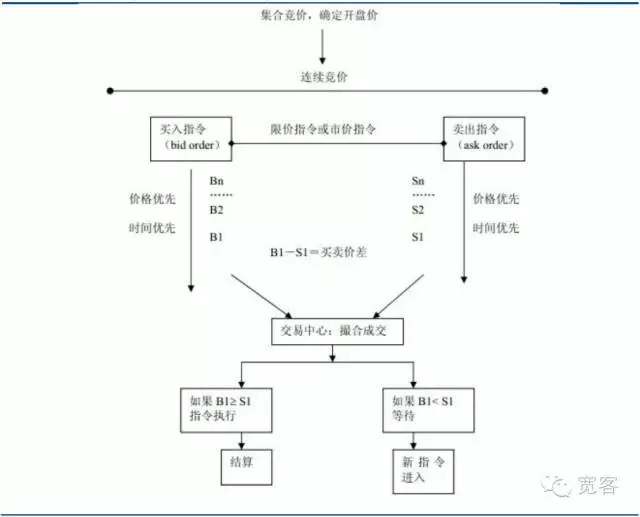  그림 1 주문을 주도하는 시장 지도

  • 1) 한정 가격 책상 주문서 소개

    주문책의 연구는 시장 미세구조 연구 범주에 속하며, 시장 미세구조 이론은 미세경제학에서의 가격 이론과 제조사 이론을 그 사상의 근원으로 삼고, 그 핵심 문제인 금융자산 거래와 그 가격 형성의 과정과 원인을 분석하는 데에는 일반적인 균형, 지역 균형, 기한수익, 기한비용, 시장 연속성, 재고 이론, 게임론, 정보경제학 등 다양한 이론과 방법을 사용한다.

    해외 연구의 발전에서 볼 때, 시장 미시스트럭처 영역은 오하라로 대표되며, 대부분의 이론은 재고 모델과 정보 모델과 같은 시장 (즉, 제안 추진 시장) 을 기반으로합니다. 올해, 실제 거래 시장에서 주문 추진이 점차 점유하고 있지만 주문 추진 시장에 대한 연구가 거의 없습니다.

    국내 증권시장과 선물시장은 모두 주문동력시장이며, 아래 그림은 주식 지표 선물계약 IF1312의 Level_1 시장 주문책 스크린입니다. 위에서 직접 얻은 정보는 많지 않으며, 기본 정보는 구매 가격, 판매 가격, 구매량 및 판매량입니다. 해외의 일부 학술 논문에서 주문책과 대응하는 정보책도 있으며, 가장 세밀한 주문 촬영 데이터를 포함하고, 각 주문의 주문량, 배달 가격, 주문 유형 정보 등이 포함됩니다. 국내 시장에서 공개된 정보책의 정보가 없기 때문에 초고속 거래는 주문책에만 의존 할 수 있습니다.

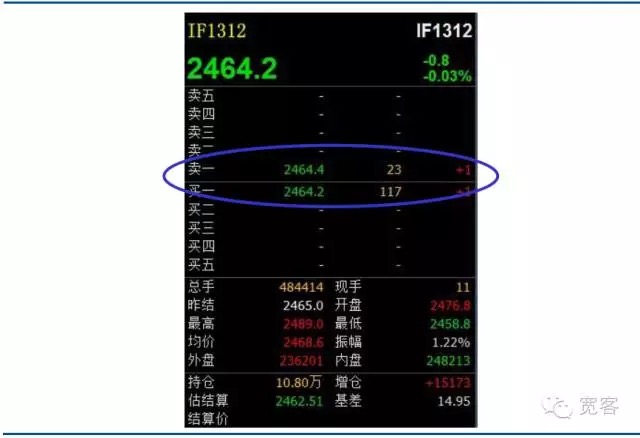    그림 2 주식 지수 미래 주식 계약 레벨-1 주문번호부

  • 2) 주문책 고주파 거래 연구 진행

    주문책의 동적 모델링에는 두 가지 방법이 있다. 하나는 고전적인 측정경제학 방법이고 다른 하나는 기계학습 방법이다. 측정경제학 방법은 고전적인 주류 연구 방법 중 하나로, 예를 들어, 가격차별 분석을 연구하는 MRR 분해, Huang 및 Stoll 분해, 주문 지속 기간을 연구하는 ACD 모델, 가격 예측을 연구하는 Logistic 모델이다.

    머신러닝은 금융 분야에서 학술 연구도 매우 활발하다. 예를 들어 2012년?? Forecasting trends of high_frequency KOSPI200 index data using learning classifiers?? 는 기술 분석의 일반적인 지표 (MA, EMA, RSI 등) 를 사용하여 머신러닝의 분류 방법을 도입하여 시장 예측을 하는 일반적인 연구 아이디어이다. 그러나 이러한 방법은 주문록의 동적 정보에 대한 채굴이 부족하다. 즉, 주문록의 동적 정보를 사용하여 높은 유동 트레이드를 수행하는 연구는 국내외에서 상대적으로 적어 있어 깊이 연구할 가치가 있는 분야이다.

• 두 번째, 주문부에서 높은 주파수 거래에서 기계 학습의 응용

  • 1) 시스템 구조

    아래 그림은 전형적인 기계 학습 거래 전략의 시스템 아키텍처이며, 주문록 데이터, 특징 발견, 모델 구축 및 검증 및 거래 기회의 몇 가지 주요 모듈을 포함합니다.

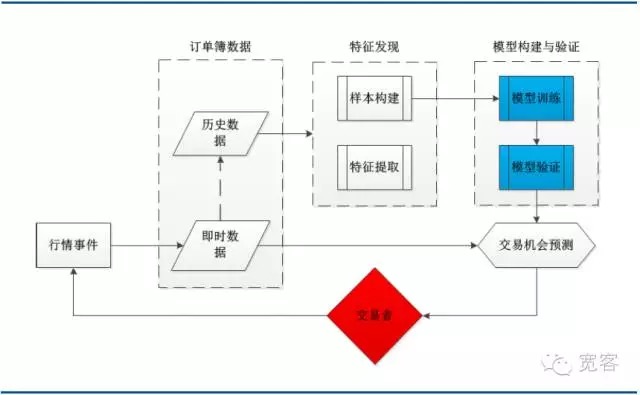    그림 3 기계 학습에 기반한 주문부 모델링 시스템 구조

  • 2) 벡터 기계를 지원하는 설명서

    1970년대에, 바프니크 등이 비교적 완성된 이론 체계인 통계학 학습 이론 (SLT, Statistical Learning Theory) 을 구축하기 시작하였다. 이 이론은 제한된 표본 상황에서 통계 법칙과 학습 방법의 특성을 연구하기 위해 사용되었으며, 제한된 표본의 기계 학습 문제에 대한 좋은 이론적 틀을 구축하여, 작은 표본, 비선형, 고차원 수와 지역 극소점과 같은 실제 문제를 더 잘 해결하였다. 1995년, 바프니크 등이 새로운 일반 학습 방법을 명확히 제시한 후, 이 이론은 광범위한 주목을 받았으며, 다양한 분야에 적용되었으며, 초기에는 방법보다 많은 우위를 나타냈다.

    SVM은 선형분해 가능한 경우에 최적의 분류 초평면에서 발전되었다. 두 가지 분류 문제에 대해 훈련 샘플 세트를 ((xi,yi), i=1,2...l, l는 훈련 샘플의 개체, xi는 훈련 샘플이며, yi는 입력 샘플 xi의 분류 표지 (예측 출력) 이다.

    최적의 분류 초평면은 모든 표본을 올바르게 분리할 수 있을 뿐만 아니라, 두 범주 사이의 가장 큰 범위를 만들 수 있다. 범위를 훈련 데이터 세트에서 해당 분류 초평면으로 가장 작은 거리의 합으로 정의한다. 최적의 분류 초평면은 테스트 데이터의 평균 분류 오류가 최소라는 것을 의미한다.

    만약 d차원 벡터 공간에 초평면이 존재한다면:

    F(x) =w*x+b=0

    위의 두 종류의 데이터를 분리할 수 있는 경우, 이 초평면을 분할 인터페이스라고 한다. 여기서 w*x는 2차원 벡터 공간의 두 벡터 w와 x의 내분자이다.

    만약 인터페이스가 나뉘면:

    w*x+b=0

    이 분포 인터페이스의 가장 가까운 두 종류의 샘플 사이의 거리를 최대화할 수 있는 분포 인터페이스는 최우선 분포 인터페이스라고 불린다.

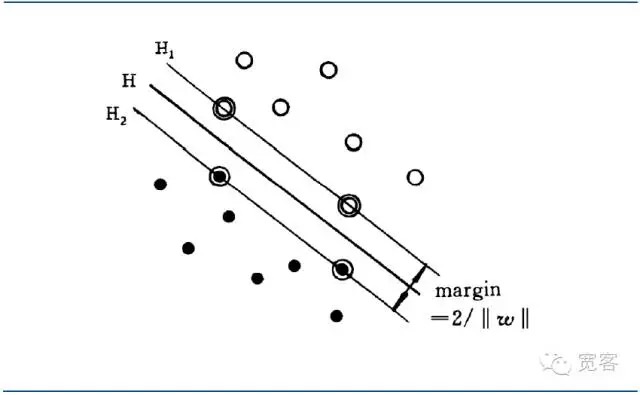    도4 SVM 2차원 최우수분석 인터페이스 도표

    최우선분해 인터페이스 방정식을 통일하여 두 종류의 샘플 사이의 거리를 만들 수 있습니다.

    

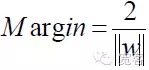
    그래서 어떤 표본에 대해서도

    

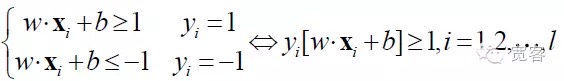
    가장 우수한 인터페이스를 얻으려면 위의 공식을 만족하는 것 외에도 최소화해야 합니다.

    따라서 SVM 문제의 수학 모형은 다음과 같습니다.

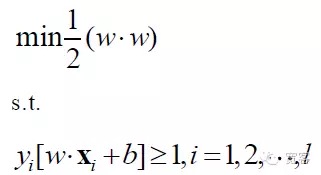
    결국 SVM은 가장 최적화된 계획 문제로 변했고, 학계의 연구 화두는 주로 신속한 해결, 다중 범주로 보급, 실제 문제 응용 등에 집중되었다.

    SVM은 초기에는 이분법 문제를 위해 제안되었으며, 현재 실제 응용의 요구에 따라 다분법 문제로 확대되었다. 기존의 다분법 알고리즘은 1대 2가, 1대 1가, 오류 수정 코딩, DAG-SVM, 그리고 다중 i-class SVM 분류기 등이 있다.

  • 3) 주문책 지표 추출

    주식 지표 선물 레벨-1 시장을 예로 들면, 주문서는 주로 구매, 판매, 구매, 판매 등의 기본 지표들을 포함하고, 깊이, 기울기, 상대적 가격 차이 등의 지표들을 파생할 수 있으며, 다른 지표들은 보유량, 거래량, 기하급수 등을 포함하며 총 17개의 지표를 포함하고 있다.

    표 1 레벨 시장 주문기록을 기반으로 한 지표 데이터베이스

    

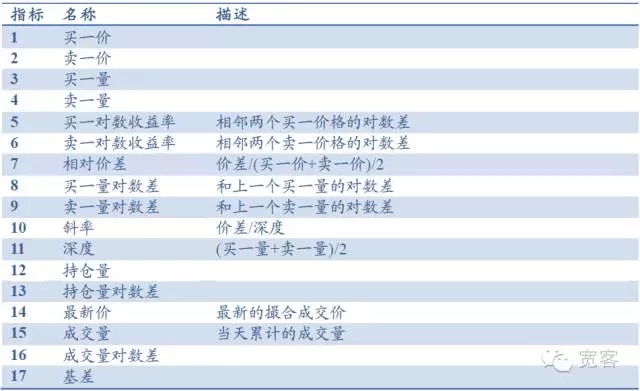
  • 4) 주문책의 역동적 특성과 거래 기회

    시장 미시경에서, 짧은 시간에 가격운동을 측정하는 두 가지 방법이 있다. 하나는 중간 가격운동이며 다른 하나는 가격차례 교차이다. 이 문서에서는 더 간단하고 직관적인 중간 가격운동을 선택한다. 중간 가격의 정의:

    

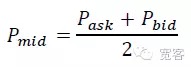
    주문책에 따라 Δt 내의 중간 가격의 ΔP 변화의 크기는 세 가지 범주로 나다.

    아래 그림은 주력계약 IF1311의 10월 29일 중간 가격 움직임의 분포이며, 하루 3,2400개의 틱 시장 데이터가 있습니다.

    Δt=1tick의 경우, 중간 가격의 변동의 절대값은 0.2가 약 6000번, 변동의 절대값은 0.4가 약 1500번, 변동의 절대값은 0.6가 약 150번, 변동의 절대값은 0.8가 50번, 변동의 절대값은 1가 약 10번이다.

    Δt=2tick의 경우, 중간 가격 변동의 절대값은 0.2가 약 7000번, 변동의 절대값은 0.4가 약 3000번, 변동의 절대값은 0.6가 약 550번, 변동의 절대값은 0.8가 약 205번, 변동의 절대값은 1보다 더 큰 약 10번이다.

    우리는 변동의 절대값이 0.4보다 크면 잠재적인 거래 기회라고 생각합니다. Δt=1tick의 경우, 하루에 약 1700개의 기회가 있습니다. Δt=2tick의 경우, 하루에 약 4000개의 기회가 있습니다.

    

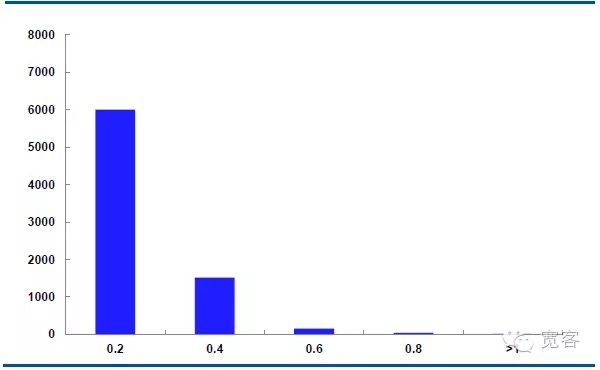
    그림 5 IF1311 10월 29일 중간 가격 변화 분포 (Δt=1tick)

    

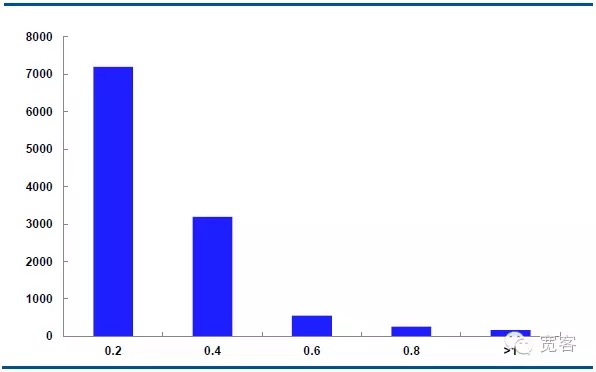
    그림 6 IF1311 10월 29일 중간 가격 변화 분포 (Δt=2tick)

• 세번째, 전략적 증거

  SVM 모델은 큰 표본 조건에서 훈련의 복잡성이 높고 훈련 시간이 길기 때문에, 우리는 IF1311 계약의 10월의 레벨_1 시장 데이터로 모델의 유효성을 검증하기 위해 비교적 짧은 기간의 역사적 시장 데이터 스프레스를 선택했습니다.

  • 1) 모델 효과 검사

    데이터 사이클: 10월 IF1311 계약 시장 데이터

    Δt 값 추출: Δt가 작을수록 거래 세부 사항에 대한 요구가 높으며, Δt=1tick의 경우 실제 거래에서 수익을 얻는 것이 어렵습니다. 모델의 효과를 비교하기 위해 각각 1tick, 2tick, 3tick을 추출합니다.

    모델 평가 지표: 샘플 정확성, 검사 정확성, 예측 시간.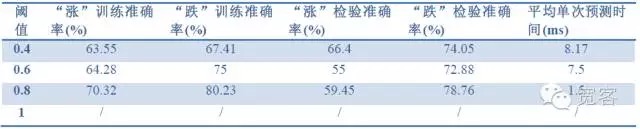표 2 1tick 데이터로 1tick의 효과를 예측합니다

    표 3 1 틱 데이터로 틱 2의 효과를 예측합니다

    테이블 4 2tick 데이터로 2tick의 효과를 예측합니다

    이 세 가지 표의 데이터에서 우리는 다음과 같은 결론을 내릴 수 있습니다. 가장 높은 정확도는 약 70%이며, 60%의 정확도는 거래 전략으로 변환 될 수 있습니다.

  • (2) 전략적 모방 수익

    예를 들어, 10월 31일, 우리는 시뮬레이션 거래를 수행하고, 기관의 주식 선물 거래 수수료는 일반적으로 기관의 주식 선물 거래 수수료는 일반적으로 0.26/10000입니다. 우리는 거래 횟수가 제한되지 않는다고 가정하고, 거래 한 번에 단편 슬라이드 가격이 0.2 포인트이며, 단편 손수는 1 명이라고 가정합니다.

    표 5 모방 전략 10월 31일 거래 상황

    하루 중 605번의 거래, 절차를 포함, 339번의 수익, 승률 56%, 순이익 11814.99원.

    이론적으로 유리는 14,520원이며, 이 부분은 전략적 실전의 핵심이다. 하위 주문 세부사항을 더 세밀하게 제어하면 유리는 감소하여 순이익을 증가시킬 수 있다. 하위 주문 세부사항이 적절하게 제어되지 않거나 시장의 변동이 이상하다면 유리는 더 커지고 순이익은 감소한다. 따라서 고주파 거래의 성공은 세부사항의 실행에 의존하는 경우가 많다.

    그림 7 10월 31일 모방 전략의 수익

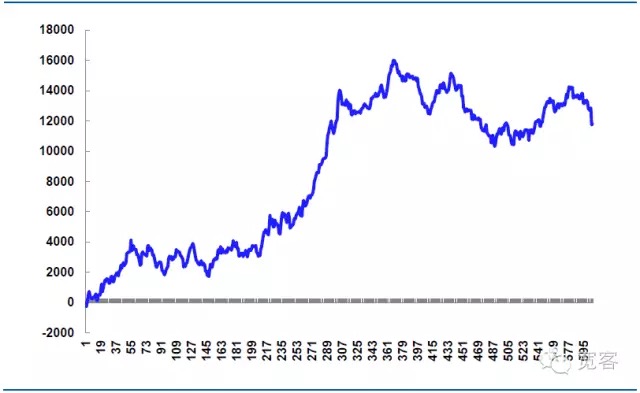
원본: 이 문서의 저자, 원본을 참조하십시오.