Naive Bayes에 대한 흥미로운 이해

NavieBayes

  생활의 많은 상황에서 분류를 사용해야 합니다. 뉴스 분류, 환자 분류 등과 같은 실제 사용 시나리오. 시각적으로 이해할 수 있도록 하기 위해, 이 글은 실제 응용에서 시작하여 간단한 일반적인 분류 알고리즘을 소개합니다.

• 01 환자 분류의 예

예를 들어서 시작해 보겠습니다. 베이즈 분류기는 아주 잘 이해가 되는데, 어렵지 않습니다. 한 병원에서 아침에 6명의 입원 환자를 입원시켰습니다. 아래의 표는 이렇습니다.

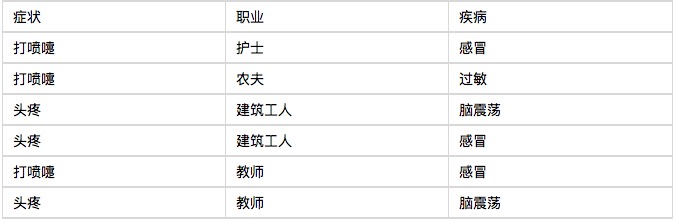
이제 일곱 번째 환자가 있습니다. 건물을 짓는 노동자입니다. 그는 감기에 걸릴 확률이 얼마나 될까요? 베이스의 법칙에 따르면:

  P(A|B) = P(B|A) P(A) / P(B)

“아뇨, 아닙니다.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

‘스피어’와 ‘건축 노동자’의 특성은 독립적이라고 가정하면, 위의 식은

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

이것은 계산할 수 있습니다.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

그래서, 이 콧물 뱉는 건설 노동자는 감기에 걸린 확률이 66%에 달한다. 마찬가지로, 이 환자가 알레르기나 뇌진탕에 걸린 확률을 계산할 수 있다. 이 확률을 비교하면 그가 가장 많이 걸린 질병이 무엇인지 알 수 있다.

이것이 베이즈 분류기의 기본적인 방법이다: 통계 자료를 바탕으로 특정 특성에 따라 각 범주의 확률을 계산하여 분류를 실현한다.

• 02 순수 베이스 분류기의 공식

어떤 개체가 n개의 특징을 가지고 있다고 가정하면, 각각 F1, F2,…,Fn. m개의 카테고리가 각각 C1, C2,…,Cm. 베이스 분류자는 가장 큰 확률을 계산하는 분류이며, 이는 다음과 같은 수식의 최대값이다:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

P ((F1F2…Fn) 는 모든 범주에 대해 동일하기 때문에, 방치할 수 있고, 문제는 求 (求) 로 바뀌게 됩니다.

  P(F1F2...Fn|C)P(C)

최대 값

순수 베이스 분류기는 더 나아가 모든 특성이 서로 독립적이라고 가정하고, 따라서

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

상술한 식의 우변에 있는 각 항은 통계 자료에서 얻을 수 있으며, 이를 통해 각 범주에 해당하는 확률을 계산하여 가장 큰 확률이 있는 범주를 찾아낼 수 있다.

“모든 특징이 서로 독립적”이라는 가정은 현실에서 성립할 가능성이 높지 않지만, 계산을 크게 단순화 할 수 있으며, 분류 결과에 대한 정확도에 큰 영향을 미치지 않는 연구가 있습니다.

다음 두 가지 예에서, 순수 베이시스 분류자를 어떻게 사용할 수 있는지 알아봅시다.

• 03 계정 분류

한 커뮤니티 웹사이트의 샘플 통계에 따르면, 10,000개의 계정 중 89%가 진짜 계정 (C0로 설정) 이며 11%가 가짜 계정 (C1로 설정) 이다. 다음으로, 계정의 진실성을 판단하기 위해 통계 자료를 사용해야 한다.

  C0 = 0.89 C1 = 0.11

어떤 계정에는 다음의 세 가지 특징이 있다고 가정해 봅시다. F1: 일기 수/기록일 수 F2: 친구 수/기록일 F3: 진짜 헤드 이미지를 사용하든가 (진짜 헤드 이미지는 1, 비진짜 헤드 이미지는 0) F1 = 0.1  F2 = 0.2  F3 = 0

이 계정은 진짜 계정인지 가짜 계정인지 물어보세요. 방법은 단순 베이시스 분류기를 사용하여 아래의 계산법의 값을 계산하는 것입니다.

P(F1|C)P(F2|C)P(F3|C)P©

위의 값들은 통계 자료에서 얻을 수 있지만, 여기서 문제가 있습니다: F1와 F2는 연속적인 변수이며, 특정 값에 따라 확률을 계산하는 것은 적절하지 않습니다. 하나의 기술은 연속적인 값을 이산 값으로 바꾸고, 간격의 확률을 계산하는 것입니다. 예를 들어 F1을[0, 0.05]、(0.05, 0.2)、[0.2, +∞] 세 개의 영역, 그리고 각각의 영역의 확률을 계산한다. 우리의 예에서, F1은 0.1이고, 두 번째 영역에 떨어지므로, 계산할 때, 두 번째 영역의 발생 확률을 사용한다.

통계자료에 따르면,

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

따라서

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 보시다시피, 이 사용자는 진짜 아이디를 사용하지 않았지만, 가짜 계정보다 30배 이상 더 많은 확률로 진짜 계정이라고 판단할 수 있습니다.

• 04 성별 분류

다음은 인간의 신체 특징에 대한 통계입니다.

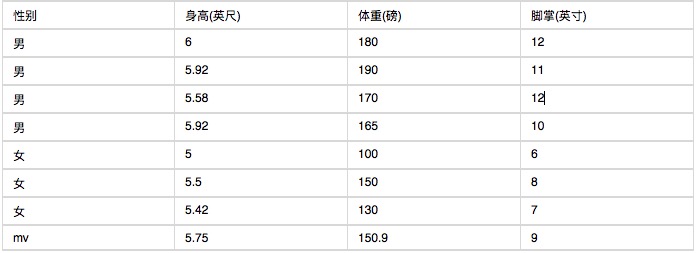
6피트, 130파운드, 8인치의 손바닥을 가진 사람이라는 것을 알고 있다면, 그 사람이 남자인지 여자인지 물어보세요. 순진한 베이츠 분류기로 아래의 공식의 값을 계산해 보세요.

P (고도와 성별) x P (체중과 성별) x P (발과 손바닥의 성별) x P (성별)

여기서의 어려움은, 키, 체중, 손바닥이 연속적인 변수이기 때문에, 분산 변수의 방법을 사용하여 확률을 계산할 수 없다는 것입니다. 그리고 표본이 너무 적기 때문에, 간격 계산도 할 수 없습니다. 어떻게 할 것인가? 이 경우, 남성과 여성의 키, 체중, 손바닥이 정형 분포라고 가정할 수 있으며, 표본을 통해 평균과 차등을 계산할 수 있습니다. 즉, 정형 분포의 밀도 함수를 얻습니다. 밀도 함수가 있으면, 대수 값을 입력하여 특정 지점의 밀도 함수의 값을 계산할 수 있습니다.

이 자료를 가지고 성별별을 계산할 수 있습니다.

P (높이=6명의 남자) x P (중량=130명의 남자) x P (발가락=8명의 남자) x P (남자)

= 6.1984 x e-9

P (높이=6명의 여성) x P (중량=130명의 여성) x P (발바닥=8명의 여성) x P (여성)

= 5.3778 x e-4

그리고 그 결과, 여성이 남성보다 거의 1만 배나 더 많은 확률로 여성이라고 판단할 수 있습니다.

위키백과 공용번호 (一峰)