PS: 이 글은 길고, 길고, 길고, 길고, 길고, 길고, 길고, 길고, 길고, 길고, 길다.

격자거래법은 본질적으로 하락과 하락, 반복적인 하락과 하락의 가격 변동에 대한 기계적 조작을 수행하는 거래 방법이다. 가격이 떨어지면 분기 구매를 하고, 가격이 상승하면 분기 판매를 한다. 격자거래법은 인위적인 사고에 의존하지 않고, 완전히 절차적 행동이다. 낚시망과 같이, 현상의 변동을 이용한 격자 간 구역에서 하락과 하락을 하고, 반복적인 순환 차등 가격을 통해 이익을 얻는다.

격자 거래법은 프로그래밍 작업을 할 수 있고, 오랜 시간을 투자하지 않고, 안전하고, 수익이 안정적입니다. 따라서 격자 거래법은 일반인이 참여하는 가장 적합한 안정적인 수익 방법입니다. 왜냐하면 이 방법은 사람의 기술 경험이 요구되는 것이 낮고, 보편성이 강하며, 특히 주식 시장에서 돈을 벌지 못하는 친구에게 적합합니다.

격자 거래법의 거래 규칙에 대한 설명

간단한 예시: 먼저 돈을 두 부분으로 나누고: 한 부분은 즉시 당신이 좋아하는 주식이나 펀드를 구입하고, 나머지 부분은 주머니에 보관합니다. 당신이 구입한 주식이나 펀드가 계속 떨어지면, 주머니의 돈을 꺼내서 더 넣습니다. 반대로, 당신이 구입한 주식이나 펀드가 부실하면, 일부를 팔고, 돈을 주머니에 넣습니다. 구체적인 규칙 세부 사항 많은 거래 소프트웨어가 내장되어 있으며, 사용자는 간단한 설정으로 자동화 운영 할 수 있습니다. 격자 거래법 우주 칼럼 시리즈 기사는 설정 교과서가 게시되어 있으며, 관심있는 친구는 칼럼 내용을 검색하여 직접 소프트웨어 설정 교과서를 학습 할 수 있습니다.

그레이트 트레이딩 방식의 다양한 변종은 많지만, 그 중 가장 유명한 변종은 다음과 같습니다. 그레이트 트레이딩 방식은 안정적으로 돈을 버는 과학적인 원리를 소개하고, 왜 당신의 계좌에 돈이 점점 더 많이 들어오는지를 설명합니다.

모든 주식을 파는 사람들은 이런 경험을 가지고 있습니다. 한 주식은 쉽게 올라가지 못하고, 다시 원래 가격으로 떨어집니다. 한 주식은 억울하게 후회하고, 빨리 팔았으면 좋겠어요. 사실 후회할 필요가 없습니다. 세계에서 가장 위대한 과학자 중 한 명인 정보학의 발명가인 샤논은 우리에게 해결책을 제시했습니다.

은 후반에 주로 투자에 관한 연구를 하며, 종종 다양한 강연을 통해 사람들에게 비밀 기술을 가르쳤다. 한 해, 은 MIT의 가장 큰 강당에서 강연을 통해 사람들에게 위의 상황에서 돈을 버는 방법에 대한 비밀을 가르쳤다.

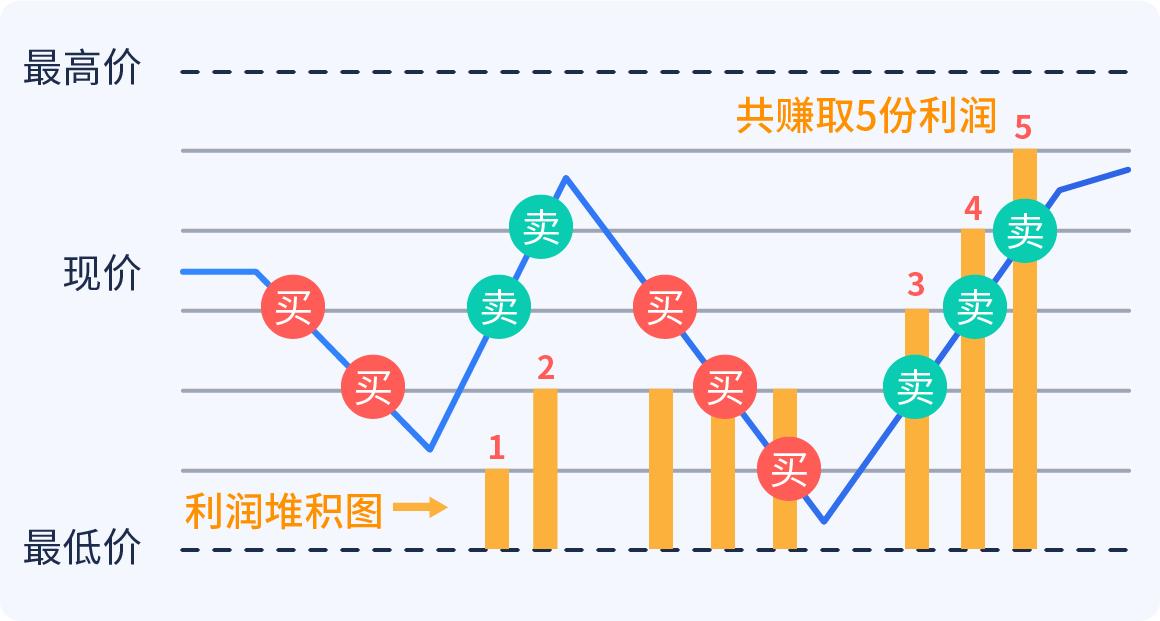
이 수수께끼의 후배들은 이것을 샤논의 악마라고 부르는데, 샤논의 악마는 우리가 흔히 말하는 격자 거래법 중 하나다.

노의 레시피는 다음과 같습니다.

만약 한 주가가 1에서 2로 올라갔다가 2에서 1로 내려갔다면 어떻게 해야 할까요?

만약 당신이 200달러를 투자하려고 한다면, 슨의 요리는 100달러를 주식과 100달러를 매장하고, 그 다음에 당신이 해야 할 일은 주식의 시장가치와 총 현금의 양을 유지하는 것입니다.

예를 들어, 100개의 주식이 200개로 올라갈때, 200개의 주식과 100개의 현금, 그리고 300개의 자산이 있을때, 당신은 50달러의 주식을 팔고, 150개의 주식과 150개의 현금을 갖게 됩니다. 그리고 주식이 1개로 떨어질때, 주식의 시장가치는 75달러입니다. 하지만 당신의 자산은 225달러입니다.

만약 주가가 먼저 하락하고 다시 올랐다면, 당신은 25달러를 얻었을 것입니다.

이건 불가능한 것처럼 들리지만, 주가가 1배나 올라갔고, 하락의 반도 하락은 2×0.5-1=0이 되는데, 어떻게 해서든 원래의 위치로 돌아가는 것이 좋지만, 슨의 전략은 실제로 돈을 벌었습니다.

넌이 돈을 벌 수 있었던 비결은 우주에서 가장 큰 턱을 가진 켈리 공식을 사용했다는 것입니다.

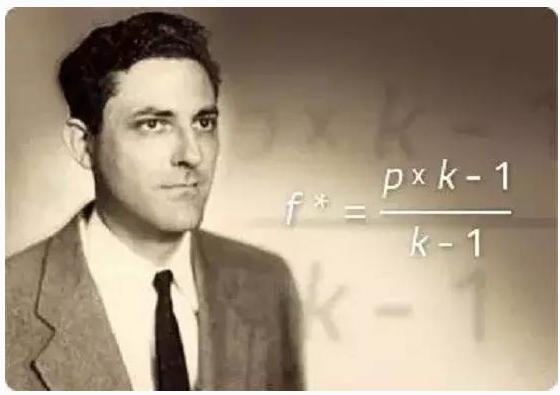
이 공식은 논의 벨 연구소의 동료인 켈리가 논의 정보론에 기초하여 통신 신호를 처리하는 응용 프로그램에서 투자하기 위해 인용한 것이다. 논의 위의 전략은 이 공식을 이용한 것이다.

케일리 공식은 투자계에서 유명한 별명인 재산 공식으로, 이 공식은 도박이나 투자에서 손실 확률에 따라 최적의 투자 비율을 계산하는 방법에 대한 문제를 다룬다.

케일리 공식의 일반적인 공식은 다음과 같다: f=(pb-q) /b

동전을 던지는 것을 예로 들자면, P는 당신이 돈을 이기는 확률입니다. q는 당신이 돈을 잃는 확률입니다. 동전을 던지는 게임에서, 이 두 값은 모두 0.5입니다. b는 무엇입니까? b는 당신이 이길 확률입니다.

예를 들어, 당신이 매번 1개를 내기 위해 6개를 내면, b는 5개와 같고, 6개를 빼면 1개를 내면, f=5×0.5-0.⁵⁄₅=40%입니다. 이 경우, 매번 40%를 내기 때문에, 앞으로의 기하학적인 수익률은 최대입니다.

어떤 투자비율도 켈리 수식보다 낫지 않습니다!

켈리 공식은 매우 간단합니다. 여러분의 자산의 미래 총 가치에 대한 설명입니다. C= (-1+fb) ^Np*(1-fa) ^ Nq (f: 투자 비율, b 승리할 때의 확률, a: 패배할 때의 확률, Np: 승리할 때의 수, Nq: 패배할 때의 수), C에 f를 변수로 구하면, 가장 좋은 f를 얻을 수 있다. 이 공식은: f = p/a-q/b

이 공식은 앞서 언급한 f=(pb-q) /b와 다르게 보이지만, 실제로는 동일합니다. 만약 당신이 패했을 때 완전히 패한다고 하면 (예를 들어 동전을 앞면으로 던지고, 반대면으로 나올 때, 당신은 내린 1달러를 잃게 됩니다) 그러면 a는 0과 같고, a는 0과 같을 때, 앞의 공식과 동일합니다.

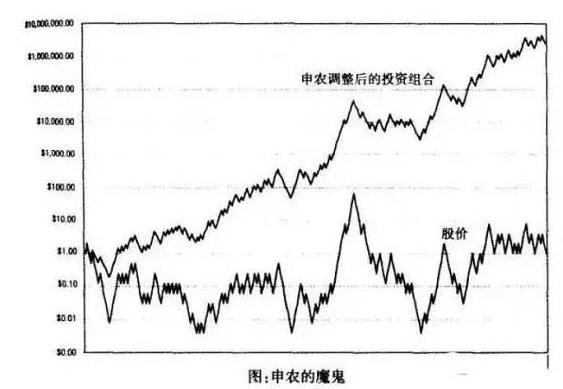
케일리 공식으로 다시 샤논의 악마를 살펴보자면, 올라갈 때 두 배로, 당신이 내기 1 조각, 승자는 당신에게 2 조각, 내려갈 때 반으로, 당신이 내기 1 조각, 패기, 승자는 5 로, 이러한 정보에 따라, 위의 케일리 공식을 사용하여 샤논의 악마의 최적의 위치를 계산할 수 있다: f = p/a-q/b = 0.⁵⁄₀.5-0.⁵⁄₁ = 0.5

이것이 바로 슨의 악의의 비밀입니다. 슨이 매번 시장가치로 조정해야 하는 이유죠. 슨의 슨의 악의의 비밀은 슨이 매번 시장가치로 조정해야 하는 이유죠. 슨의 슨의 악의의 비밀은 슨이 매번 시장가치로 조정해야 하는 이유죠.

셰넌이 이 전략을 계속한다면, 그는 얼마나 많은 돈을 벌 수 있을까요?

위에서 소개된 케일리 공식의 추론 과정을 통해 알 수 있다: C=(1+0.5×1) ^Np*(1-0.5×0.5) ^Nq, 장기적으로 상승과 하락의 확률이 같다고 가정하면, Np=Nq=n, 그 결과는 다음과 같습니다:

다른 말로 하면, 슨의 자산이 1.125의 n제곱으로 증가한다는 것은 매우 비영리적이고 무서운 것처럼 들리지 않습니까?

하지만 이건 직관과 상반되는 말이에요, 그렇죠?

이 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고, 오르내리고

만약 우리가 좀 더 자세히 살펴본다면, 1달러를 투자하면 1달러를 벌고, 1달러를 투자하면 0.5달러를 잃게 되는 오류를 발견할 수 있습니다. 확률적 기대치에 따라 계산하면 1×0.5-0.5×0.5=0.25입니다. 이 모순은 분명히 긍정적인 기대수익이 있다는 것입니다.

하지만 만약 이 게임이 긍정적인 수익을 기대하는 게임이라면, 왜 당신이 모든 돈을 가지고 있으면 결국에는 아무것도 얻지 못하고 빈 채로 남게 되는 걸까요?

이것은 매우 흥미로운 현상입니다. 당신의 최종 수익과 당신의 지분 비율은 매우 중요한 관계가 있습니다!

하지만, 만약 당신이 이 게임을 하고 있다면, 당신은 여전히 돈을 벌 수 없을 것입니다.

만약 우리가 이윤의 개념으로 샤논의 악마를 측정할 때 이윤이 2×0.5=1 (2: 곱하기, 0.5: 대등) 이라는 것을 발견한다면, 그것은 결코 이윤이 없는 게임이며, 이윤은 결코 존재하지 않을 것이다.

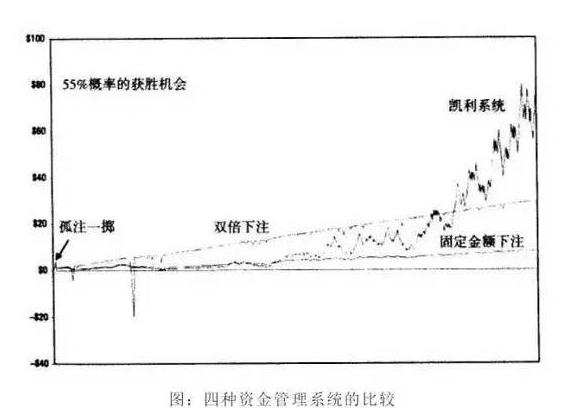
켈리 공식은 기하학적 수익률을 0으로 만들 수 있지만 무한한 부를 창조하는 마법의 공식입니다.

만약 우리가 샤논의 악마에 대해 더 깊이 생각한다면, 우리는 상승과 하락이 모두 0으로 돌아가고, 여전히 돈을 벌 수 있다고 생각할 수 있습니다. 이것은 과학적이지 않습니다. 문제는 확실히 1달러의 상승과 하락이 0.5의 확률에 있습니다.

현실에서는 아마도 이 두 가지 확률의 불균형으로 인한 착각일 것이다. 두 배의 확률은 떨어질 때 절반보다 낮을 가능성이 높다. 따라서 위의 공식의 확률을 수정하면 돈을 벌 수 없다.

그리고 논의 악마는 이 둘의 확률이 같다는 것을 암시합니다. 이 두가지 확률이 서로 다르다는 것은 합리적인 생각일 수도 있고, 그렇지 않으면 아무것도 없이 돈으로 변할 수도 있습니다.

그래서 우리가 한 번 생각해 볼 것은, 1배의 확률이 1배의 확률과 반의 확률이 같은 것인가?

한쪽은 100% 상승하고 다른 한쪽은 50% 하락했습니다. 100% 상승한 숫자는 50% 하락한 숫자보다 훨씬 작습니다.

그리고 느리게, 100%와 50%는 단지 한 폭일 뿐, 확률이 아니다. 주식 시장의 수익률에 대해, 학술과 실무는 대수학적 수익률을 채택한다. 실무는 대수학적 수익률이 정형 분포에 완벽하게 일치하지는 않지만, 결국 근접도가 매우 높다.

더 나은 모델이 나오기 전까지는 정형분포의 쌍수수수익률을 살펴보고, 직접 답을 찾아보도록 하겠습니다. 100%의 인수수익률이 올라간다는 것은 0.6931이고, 50%의 인수익률이 내려간다는 것은 0.6931입니다. 인수익률이 정형적으로 분포되어 있는 경우, 우리가 일상적으로 말하는 인수익률이 올라간다는 것과 50%가 내려간다는 것은 같은 확률입니다.

만약 확률이 같고, 장기적인 수익률이 0이라면, 당신은 논의 악마 (망 거래법) 를 이용해 돈을 벌 수 있습니다.

그래서 50개의 현금과 50개의 포지션으로 얼마나 많은 돈을 벌 수 있을까요?

10%를 더하면 인수수익률이 ln(1.1) = 0.09531이 됩니다. 이제 우리는 e^(-0.0953) = 0.909의 인수익률을 계산합니다. 10%의 확률이 떨어질 확률은 9.09%입니다. 그리고 확률은 0.5%입니다. 그리고 확률은 10%나 떨어질 확률이 있습니다.

케일리 공식으로 최적의 지분 비율을 계산하면, 우리는 논의 악마 같은 주식과 함께 할 필요가 있습니다. 팔고, 팔고, 고정 지분 비율을 유지하면, 우리는 논의 악마 같은 수익을 얻을 수 있습니다!

앞의 케일리 공식에 따라: f=p/a-q/b, 우리가 방금 계산한 확률과 확률을 가져와: f=0.⁵⁄₀.0909-0.⁵⁄₀.1=5.5005-5=0.5005, 거의 0.5에 해당한다.

그래서 케일리 공식에 따라 계산된 최적의 지분 비율은 50%의 지점입니다.

그리고, 이 모든 것은 제가 Kelley의 공식에 대해 설명하는 과정에서 이미 언급한 바와 같습니다.

C=（1+fb)^Np(1-fa) ^Nq, 우리는 방금 계산한 숫자를 대입합니다. C=(1+0.5×0.1)(1-0.5×0.0909)^n=(1.05×0.95455)^n=1.0022^n

완벽한 투자 비율 케일리 공식에 따라 설계된 기계는 진동률 19.09%의 공간에 대한 완벽한 거래를 통해 주식 시장의 상수 수익률이 정형적으로 분산되는 것을 전제로 한 거래당 0.22%의 순이익을 얻을 수 있습니다. 거래 비용을 고려하지 않고 거래 비용을 고려하지 않으면 거래 당 0.22%의 순이익을 얻을 수 있습니다.

규칙의 범위 내에서, 이 이윤률은 계좌 자금에 대한 성장 속도가 가장 빠르다. 이것은 0 기대 조건에서 그리드 거래법이 포지션 관리를 사용하여 수익을 안정화 할 수 있는 본질적인 원칙이다.

결론적으로, 격자 거래법은 좋은 거래 방법이지만, 몇 가지 단점도 있습니다. 규칙의 실패가 발생할 수 있습니다. 예를 들어, 격자 파괴의 두려움 일방적인 두려움 등과 같이, 격자 거래법을 안전하게 사용하려면 이러한 단점을 해결해야합니다.

그레트 거래법의 몇 가지 교훈을 공유합니다: https://www.fmz.cn/bbs-topic/7567 격자 거래법 거래 규칙에 대한 자세한 설명 https://www.fmz.cn/bbs-topic/7568 격자 거래법의 장단점과 전략 최적화 방법 https://www.fmz.cn/bbs-topic/7569 격자 거래법 전략 최적화 - 적절한 투자 유형을 선택하는 방법 https://www.fmz.cn/bbs-topic/7570 격자 거래법 전략 최적화 - 일방적 하락 문제를 해결하고 격자 해킹률을 낮추기 https://www.fmz.cn/bbs-topic/7571 격자 거래법 전략 최적화 - 포지션 관리를 활용하여 신속한 해제를 위한 방법 https://www.fmz.cn/bbs-topic/7572 격자 거래법 최후의 최적화 - 격자 수익도 5배로 증가할 수 있습니다. https://www.fmz.cn/bbs-topic/7524 네트워크 전략으로 고주파刷单 전략을 조작하는 아이디어