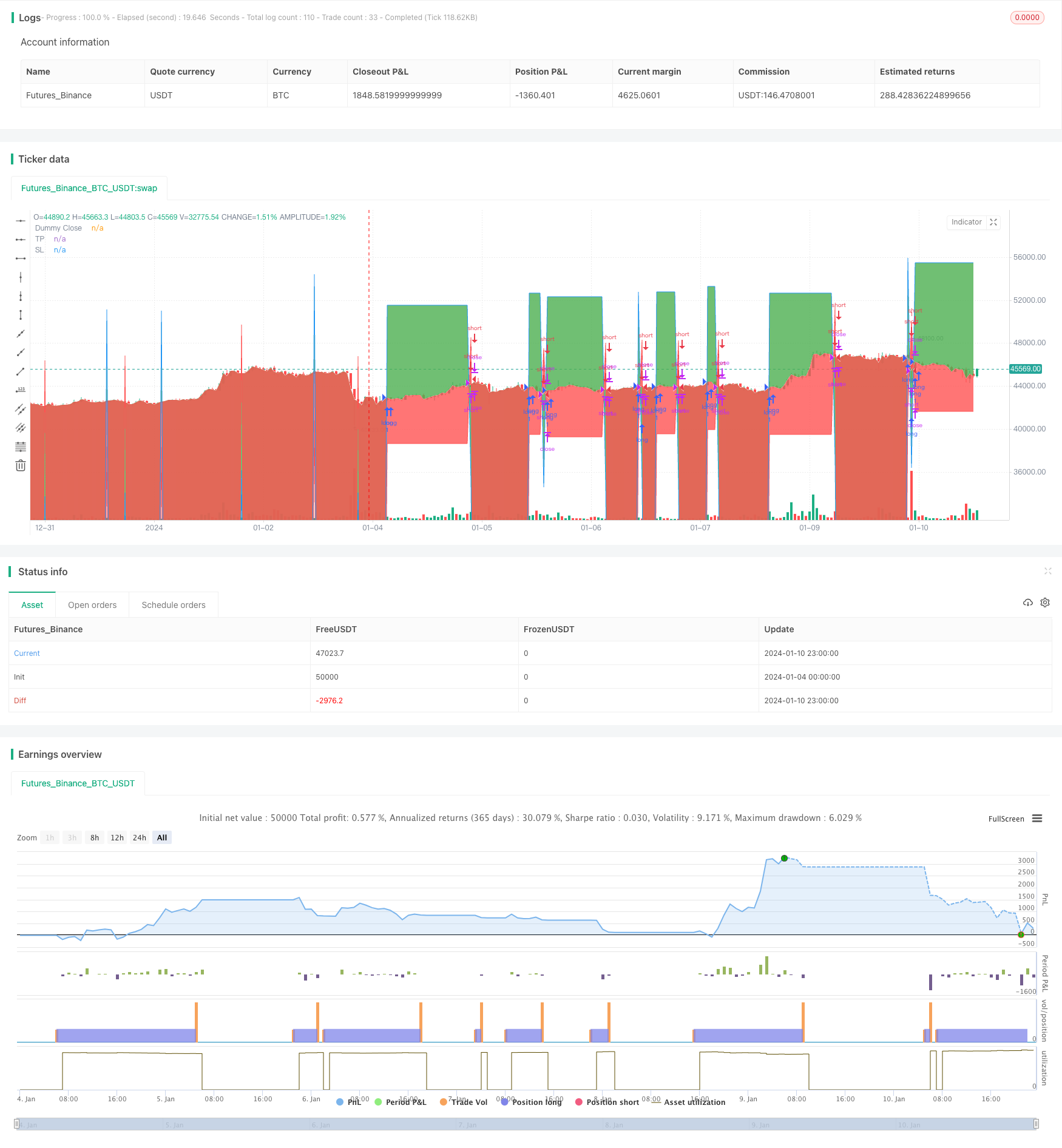
개요
이 전략은 다항적 삽입 값을 기반으로 한 RSI 운동 지표인 델타-RSI를 사용하여 거래 신호를 생성한다. 델타-RSI는 RSI를 국소적 다항적 회귀 방법을 통해 부드럽게 처리하여 RSI의 1 단계 시간 배수를 얻으며 운동 지표로 사용한다. 이 전략은 ATR, 교차량 및 RSI를 기반으로 한 필터를 추가하여 가짜 신호의 일부를 필터링 할 수 있다.
원칙
이 전략의 핵심 지표는 델타-RSI입니다. 계산 단계는 다음과 같습니다.
- rsi_l 주기의 길이를 가진 RSI 시퀀스를 입력합니다.
- 길이가 window인 슬라이딩 윈도우에서 RSI를 다항적 삽입값 방법을 사용하여 적용합니다.
- 현재 지점에서의 1차 계수인 델타-RSI를 계산하기
- 델타-RSI 상단 0은 구매 신호이고, 하단 0은 판매 신호입니다.
- 델타-RSI의 신호선과 결합하여 거래 신호를 생성할 수도 있다.
ATR, 거래량, RSI 필터로 신호를 필터링하는 전략:
- ATR 필터: 현재 N주기 ATR이 M주기 ATR보다 높으며, 변동률이 상승하는 것을 나타냅니다.
- 거래량 필터: 현재 거래량은 근 M주기 평균 거래량 N배를 초과한다
- RSI 필터: RSI가 1보다 높고 2보다 낮아 오버 바이 오버 셀 영역을 필터링한다
장점
이 전략은 다음과 같은 장점을 가지고 있습니다.
- 델타-RSI 지표는 트렌드 전환을 더 빨리 잡을 수 있습니다.
- 필터를 추가하여 대부분의 가짜 신호를 필터링하여 신호 품질을 향상시킵니다.
- 다양한 시장 환경에 맞게 사용자 정의 가능한 다항식 삽입값 및 필러 변수
- 개인 취향에 맞게 더 많은 시간을 할애할 수 있습니다.
- 단편적 손실과 수익을 제어하기 위해 단편적 손실을 제어할 수 있습니다.
위험
이 전략에는 다음과 같은 위험도 있습니다.
- 매개 변수 설정이 잘못되면 지나치게 부드러워지거나 지나치게 필터링 될 수 있습니다.
- 상위위권 손실 위험 또는 상위권 손실 위험
- 단위 손실을 확대할 수 있는 스톱 손실 설정의 과잉 확장
이러한 위험은 최적화 변수, 조정 필터 조건, 더 엄격한 중지 손실을 설정하여 제어 및 감소시킬 수 있습니다.
최적화 방향
이 전략은 더욱 개선될 수 있습니다.
- 델타-RSI 모델 파라미터를 최적화하여 적합성을 개선
- 기계 학습 기반의 적응 필러링을 추가합니다.
- 다른 품종에 따라 각각 매개 변수를 설정
- 모델 포트폴리오를 늘리는 방법과 같은 안정성을 높이는 방법
요약하다
이 전략은 델타-RSI 지표의 높은 민감성 특성을 활용하여 엄격한 필터링 메커니즘과 함께 위험을 통제하는 전제 하에 전략의 품질을 향상시킵니다. 매개 변수 및 모델을 지속적으로 최적화함으로써 전략의正 수익률을 더욱 확대할 수 있을 것으로 예상되며, 효과적인 양적 거래 전략입니다.
전략 소스 코드
/*backtest
start: 2024-01-04 00:00:00
end: 2024-01-11 00:00:00
period: 1h
basePeriod: 15m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
// © tbiktag
//
// Delta-RSI Oscillator Strategy With Filters
//
// This is a version of the Delta-RSI Oscillator Strategy compatible with
// the Strategy Tester.
//
// This version also allows filtering the trade signals generated by Delts-RSI
// by means of volatility (defined by ATR), relative volume and RSI(14).
//
// Delta-RSI (© tbiktag) is a smoothed time derivative of the RSI designed
// as a momentum indicator. For the original publication, see link below:
// https://www.tradingview.com/script/OXQVFTQD-Delta-RSI-Oscillator/
//
// D-RSI model parameters:
// RSI Length: The timeframe of the RSI that serves as an input to D-RSI.
// Frame Length: The length of the lookback frame used for local regression.
// Polynomial Order: The order of the local polynomial function used to interpolate
// the RSI.
// Trade signals are generated based on three optional conditions:
// - Zero-crossing: bullish when D-RSI crosses zero from negative to positive
// values (bearish otherwise)
// - Signal Line Crossing: bullish when D-RSI crosses from below to above the signal
// line (bearish otherwise)
// - Direction Change: bullish when D-RSI was negative and starts ascending
// (bearish otherwise)
//
//@version=4
strategy(title="Delta-RSI Strategy with Filters", shorttitle = "D-RSI with filters", overlay = true)
// ---Subroutines---
matrix_get(_A,_i,_j,_nrows) =>
// Get the value of the element of an implied 2d matrix
//input:
// _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _i :: integer: row number
// _j :: integer: column number
// _nrows :: integer: number of rows in the implied 2d matrix
array.get(_A,_i+_nrows*_j)
matrix_set(_A,_value,_i,_j,_nrows) =>
// Set a value to the element of an implied 2d matrix
//input:
// _A :: array, changed on output: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _value :: float: the new value to be set
// _i :: integer: row number
// _j :: integer: column number
// _nrows :: integer: number of rows in the implied 2d matrix
array.set(_A,_i+_nrows*_j,_value)
transpose(_A,_nrows,_ncolumns) =>
// Transpose an implied 2d matrix
// input:
// _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _nrows :: integer: number of rows in _A
// _ncolumns :: integer: number of columns in _A
// output:
// _AT :: array: pseudo 2d matrix with implied dimensions: _ncolums x _nrows
var _AT = array.new_float(_nrows*_ncolumns,0)
for i = 0 to _nrows-1
for j = 0 to _ncolumns-1
matrix_set(_AT, matrix_get(_A,i,j,_nrows),j,i,_ncolumns)
_AT
multiply(_A,_B,_nrowsA,_ncolumnsA,_ncolumnsB) =>
// Calculate scalar product of two matrices
// input:
// _A :: array: pseudo 2d matrix
// _B :: array: pseudo 2d matrix
// _nrowsA :: integer: number of rows in _A
// _ncolumnsA :: integer: number of columns in _A
// _ncolumnsB :: integer: number of columns in _B
// output:
// _C:: array: pseudo 2d matrix with implied dimensions _nrowsA x _ncolumnsB
var _C = array.new_float(_nrowsA*_ncolumnsB,0)
int _nrowsB = _ncolumnsA
float elementC= 0.0
for i = 0 to _nrowsA-1
for j = 0 to _ncolumnsB-1
elementC := 0
for k = 0 to _ncolumnsA-1
elementC := elementC + matrix_get(_A,i,k,_nrowsA)*matrix_get(_B,k,j,_nrowsB)
matrix_set(_C,elementC,i,j,_nrowsA)
_C
vnorm(_X,_n) =>
//Square norm of vector _X with size _n
float _norm = 0.0
for i = 0 to _n-1
_norm := _norm + pow(array.get(_X,i),2)
sqrt(_norm)
qr_diag(_A,_nrows,_ncolumns) =>
//QR Decomposition with Modified Gram-Schmidt Algorithm (Column-Oriented)
// input:
// _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _nrows :: integer: number of rows in _A
// _ncolumns :: integer: number of columns in _A
// output:
// _Q: unitary matrix, implied dimenstions _nrows x _ncolumns
// _R: upper triangular matrix, implied dimansions _ncolumns x _ncolumns
var _Q = array.new_float(_nrows*_ncolumns,0)
var _R = array.new_float(_ncolumns*_ncolumns,0)
var _a = array.new_float(_nrows,0)
var _q = array.new_float(_nrows,0)
float _r = 0.0
float _aux = 0.0
//get first column of _A and its norm:
for i = 0 to _nrows-1
array.set(_a,i,matrix_get(_A,i,0,_nrows))
_r := vnorm(_a,_nrows)
//assign first diagonal element of R and first column of Q
matrix_set(_R,_r,0,0,_ncolumns)
for i = 0 to _nrows-1
matrix_set(_Q,array.get(_a,i)/_r,i,0,_nrows)
if _ncolumns != 1
//repeat for the rest of the columns
for k = 1 to _ncolumns-1
for i = 0 to _nrows-1
array.set(_a,i,matrix_get(_A,i,k,_nrows))
for j = 0 to k-1
//get R_jk as scalar product of Q_j column and A_k column:
_r := 0
for i = 0 to _nrows-1
_r := _r + matrix_get(_Q,i,j,_nrows)*array.get(_a,i)
matrix_set(_R,_r,j,k,_ncolumns)
//update vector _a
for i = 0 to _nrows-1
_aux := array.get(_a,i) - _r*matrix_get(_Q,i,j,_nrows)
array.set(_a,i,_aux)
//get diagonal R_kk and Q_k column
_r := vnorm(_a,_nrows)
matrix_set(_R,_r,k,k,_ncolumns)
for i = 0 to _nrows-1
matrix_set(_Q,array.get(_a,i)/_r,i,k,_nrows)
[_Q,_R]
pinv(_A,_nrows,_ncolumns) =>
//Pseudoinverse of matrix _A calculated using QR decomposition
// Input:
// _A:: array: implied as a (_nrows x _ncolumns) matrix
//. _A = [[column_0],[column_1],...,[column_(_ncolumns-1)]]
// Output:
// _Ainv:: array implied as a (_ncolumns x _nrows) matrix
// _A = [[row_0],[row_1],...,[row_(_nrows-1)]]
// ----
// First find the QR factorization of A: A = QR,
// where R is upper triangular matrix.
// Then _Ainv = R^-1*Q^T.
// ----
[_Q,_R] = qr_diag(_A,_nrows,_ncolumns)
_QT = transpose(_Q,_nrows,_ncolumns)
// Calculate Rinv:
var _Rinv = array.new_float(_ncolumns*_ncolumns,0)
float _r = 0.0
matrix_set(_Rinv,1/matrix_get(_R,0,0,_ncolumns),0,0,_ncolumns)
if _ncolumns != 1
for j = 1 to _ncolumns-1
for i = 0 to j-1
_r := 0.0
for k = i to j-1
_r := _r + matrix_get(_Rinv,i,k,_ncolumns)*matrix_get(_R,k,j,_ncolumns)
matrix_set(_Rinv,_r,i,j,_ncolumns)
for k = 0 to j-1
matrix_set(_Rinv,-matrix_get(_Rinv,k,j,_ncolumns)/matrix_get(_R,j,j,_ncolumns),k,j,_ncolumns)
matrix_set(_Rinv,1/matrix_get(_R,j,j,_ncolumns),j,j,_ncolumns)
//
_Ainv = multiply(_Rinv,_QT,_ncolumns,_ncolumns,_nrows)
_Ainv
norm_rmse(_x, _xhat) =>
// Root Mean Square Error normalized to the sample mean
// _x. :: array float, original data
// _xhat :: array float, model estimate
// output
// _nrmse:: float
float _nrmse = 0.0
if array.size(_x) != array.size(_xhat)
_nrmse := na
else
int _N = array.size(_x)
float _mse = 0.0
for i = 0 to _N-1
_mse := _mse + pow(array.get(_x,i) - array.get(_xhat,i),2)/_N
_xmean = array.sum(_x)/_N
_nrmse := sqrt(_mse) /_xmean
_nrmse
diff(_src,_window,_degree) =>
// Polynomial differentiator
// input:
// _src:: input series
// _window:: integer: wigth of the moving lookback window
// _degree:: integer: degree of fitting polynomial
// output:
// _diff :: series: time derivative
// _nrmse:: float: normalized root mean square error
//
// Vandermonde matrix with implied dimensions (window x degree+1)
// Linear form: J = [ [z]^0, [z]^1, ... [z]^degree],
// with z = [ (1-window)/2 to (window-1)/2 ]
var _J = array.new_float(_window*(_degree+1),0)
for i = 0 to _window-1
for j = 0 to _degree
matrix_set(_J,pow(i,j),i,j,_window)
// Vector of raw datapoints:
var _Y_raw = array.new_float(_window,na)
for j = 0 to _window-1
array.set(_Y_raw,j,_src[_window-1-j])
// Calculate polynomial coefficients which minimize the loss function
_C = pinv(_J,_window,_degree+1)
_a_coef = multiply(_C,_Y_raw,_degree+1,_window,1)
// For first derivative, approximate the last point (i.e. z=window-1) by
float _diff = 0.0
for i = 1 to _degree
_diff := _diff + i*array.get(_a_coef,i)*pow(_window-1,i-1)
// Calculates data estimate (needed for rmse)
_Y_hat = multiply(_J,_a_coef,_window,_degree+1,1)
float _nrmse = norm_rmse(_Y_raw,_Y_hat)
[_diff,_nrmse]
/// --- main ---
degree = input(title="Polynomial Order", group = "Model Parameters:",
inline = "linepar1", type = input.integer, defval=3, minval = 1)
rsi_l = input(title = "RSI Length", group = "Model Parameters:",
inline = "linepar1", type = input.integer, defval = 21, minval = 1,
tooltip="The period length of RSI that is used as input.")
window = input(title="Length ( > Order)", group = "Model Parameters:",
inline = "linepar2", type = input.integer, defval=50, minval = 2)
signalLength = input(title="Signal Length", group = "Model Parameters:",
inline = "linepar2", type=input.integer, defval=9,
tooltip="The signal line is a EMA of the D-RSI time series.")
islong = input(title = "Long", group = "Allowed Entries:",
inline = "lineent",type = input.bool, defval = true)
isshort = input(title = "Short", group = "Allowed Entries:",
inline = "lineent", type = input.bool, defval= true)
buycond = input(title="Buy", group = "Entry and Exit Conditions:",
inline = "linecond",type = input.string, defval="Signal Line Crossing",
options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
sellcond = input(title="Sell", group = "Entry and Exit Conditions:",
inline = "linecond",type = input.string, defval="Signal Line Crossing",
options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
endcond = input(title="Exit", group = "Entry and Exit Conditions:",
inline = "linecond",type = input.string, defval="Signal Line Crossing",
options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
filterlong =input(title = "Long Entries", inline = 'linefilt', group = 'Apply Filters to',
type = input.bool, defval = true)
filtershort =input(title = "Short Enties", inline = 'linefilt', group = 'Apply Filters to',
type = input.bool, defval = true)
filterend =input(title = "Exits", inline = 'linefilt', group = 'Apply Filters to',
type = input.bool, defval = true)
usevol =input(title = "", inline = 'linefiltvol', group = 'Relative Volume Filter:',
type = input.bool, defval = false)
rvol = input(title = "Volume >", inline = 'linefiltvol', group = 'Relative Volume Filter:',
type = input.integer, defval = 1)
len_vol = input(title = "Avg. Volume Over Period", inline = 'linefiltvol', group = 'Relative Volume Filter:',
type = input.integer, defval = 30, minval = 1,
tooltip="The current volume must be greater than N times the M-period average volume.")
useatr =input(title = "", inline = 'linefiltatr', group = 'Volatility Filter:',
type = input.bool, defval = false)
len_atr1 = input(title = "ATR", inline = 'linefiltatr', group = 'Volatility Filter:',
type = input.integer, defval = 5, minval = 1)
len_atr2 = input(title = "> ATR", inline = 'linefiltatr', group = 'Volatility Filter:',
type = input.integer, defval = 30, minval = 1,
tooltip="The N-period ATR must be greater than the M-period ATR.")
usersi =input(title = "", inline = 'linersi', group = 'Overbought/Oversold Filter:',
type = input.bool, defval = false)
rsitrhs1 = input(title = "", inline = 'linersi', group = 'Overbought/Oversold Filter:',
type = input.integer, defval = 0, minval=0, maxval=100)
rsitrhs2 = input(title = "< RSI (14) >", inline = 'linersi', group = 'Overbought/Oversold Filter:',
type = input.integer, defval = 100, minval=0, maxval=100,
tooltip="RSI(14) must be in the range between N and M.")
issl = input(title = "SL", inline = 'linesl1', group = 'Stop Loss / Take Profit:',
type = input.bool, defval = false)
slpercent = input(title = ", %", inline = 'linesl1', group = 'Stop Loss / Take Profit:',
type = input.float, defval = 10, minval=0.0)
istrailing = input(title = "Trailing", inline = 'linesl1', group = 'Stop Loss / Take Profit:',
type = input.bool, defval = false)
istp = input(title = "TP", inline = 'linetp1', group = 'Stop Loss / Take Profit:',
type = input.bool, defval = false)
tppercent = input(title = ", %", inline = 'linetp1', group = 'Stop Loss / Take Profit:',
type = input.float, defval = 20)
fixedstart =input(title="", group = "Fixed Backtest Period Start/End Dates:",
inline = "linebac1", type = input.bool, defval = true)
backtest_start=input(title = "", type = input.time, inline = "linebac1",
group = "Fixed Backtest Period Start/End Dates:",
defval = timestamp("01 Jan 2017 13:30 +0000"),
tooltip="If deactivated, backtest staring from the first available price bar.")
fixedend = input(title="", group = "Fixed Backtest Period Start/End Dates:",
inline = "linebac2", type = input.bool, defval = false)
backtest_end =input(title = "", type = input.time, inline = "linebac2",
group = "Fixed Backtest Period Start/End Dates:",
defval = timestamp("30 Dec 2080 23:30 +0000"),
tooltip="If deactivated, backtesting ends at the last available price bar.")
if window < degree
window := degree+1
src = rsi(close,rsi_l)
[drsi,nrmse] = diff(src,window,degree)
signalline = ema(drsi, signalLength)
// Conditions for D-RSI
dirchangeup = (drsi>drsi[1]) and (drsi[1]<drsi[2]) and drsi[1]<0.0
dirchangedw = (drsi<drsi[1]) and (drsi[1]>drsi[2]) and drsi[1]>0.0
crossup = crossover(drsi,0.0)
crossdw = crossunder(drsi,0.0)
crosssignalup = crossover(drsi,signalline)
crosssignaldw = crossunder(drsi,signalline)
// D-RSI signals
drsilong = (buycond=="Direction Change"?dirchangeup:(buycond=="Zero-Crossing"?crossup:crosssignalup))
drsishort= (sellcond=="Direction Change"?dirchangedw:(sellcond=="Zero-Crossing"?crossdw:crosssignaldw))
drisendlong = (endcond=="Direction Change"?dirchangedw:(endcond=="Zero-Crossing"?crossdw:crosssignaldw))
drisendshort= (endcond=="Direction Change"?dirchangeup:(endcond=="Zero-Crossing"?crossup:crosssignalup))
// Filters
rsifilter = usersi?(rsi(close,14) > rsitrhs1 and rsi(close,14) < rsitrhs2):true
volatilityfilter = useatr?(atr(len_atr1) > atr(len_atr2)):true
volumefilter = usevol?(volume > rvol*sma(volume,len_vol)):true
totalfilter = volatilityfilter and volumefilter and rsifilter
//Filtered signals
golong = drsilong and islong and (filterlong?totalfilter:true)
goshort = drsishort and isshort and (filtershort?totalfilter:true)
endlong = drisendlong and (filterend?totalfilter:true)
endshort = drisendlong and (filterend?totalfilter:true)
// Backtest period
//backtest_start = timestamp(syminfo.timezone, startYear, startMonth, startDate, 0, 0)
//backtest_end = timestamp(syminfo.timezone, endYear, endMonth, endDate, 0, 0)
isinrange = true
// Entry price / Take profit / Stop Loss
startprice = valuewhen(condition=golong or goshort, source=close, occurrence=0)
pm = golong?1:goshort?-1:1/sign(strategy.position_size)
takeprofit = startprice*(1+pm*tppercent*0.01)
// fixed stop loss
stoploss = startprice * (1-pm*slpercent*0.01)
// trailing stop loss
if istrailing and strategy.position_size>0
stoploss := max(close*(1 - slpercent*0.01),stoploss[1])
else if istrailing and strategy.position_size<0
stoploss := min(close*(1 + slpercent*0.01),stoploss[1])
tpline = plot(takeprofit,color=color.blue,transp=100, title="TP")
slline = plot(stoploss, color=color.red, transp=100, title="SL")
p1 = plot(close,transp=100,color=color.white, title="Dummy Close")
fill(p1, tpline, color=color.green, transp=istp?70:100, title="TP")
fill(p1, slline, color=color.red, transp=issl?70:100, title="SL")
// Backtest: Basic Entry and Exit Conditions
if golong and isinrange and islong
strategy.entry("long", true )
alert("D-RSI Long " + syminfo.tickerid, alert.freq_once_per_bar_close)
if goshort and isinrange and isshort
strategy.entry("short", false)
alert("D-RSI Short " + syminfo.tickerid, alert.freq_once_per_bar_close)
if endlong
strategy.close("long", alert_message="Close Long")
alert("D-RSI Exit Long " + syminfo.tickerid, alert.freq_once_per_bar_close)
if endshort
strategy.close("short", alert_message="Close Short")
alert("D-RSI Exit Short " + syminfo.tickerid, alert.freq_once_per_bar_close)
// Exit via SL or TP
strategy.exit(id="sl/tp long", from_entry="long", stop=issl?stoploss:na,
limit=istp?takeprofit:na, alert_message="Close Long")
strategy.exit(id="sl/tp short",from_entry="short",stop=issl?stoploss:na,
limit=istp?takeprofit:na, alert_message="Stop Loss Short")
// Close if outside the range
if (not isinrange)
strategy.close_all()