Pengujian Kembali Strategi Pasangan Pembalikan Rata-rata Intraday Antara SPY Dan IWM

Dalam artikel ini kita akan mempertimbangkan strategi perdagangan intraday pertama kita. Ia akan menggunakan idea perdagangan klasik, iaitu pasangan perdagangan. Dalam kes ini kita akan menggunakan dua Dana Perdagangan Bursa (ETF), SPY dan IWM, yang didagangkan di Bursa Saham New York (NYSE) dan cuba mewakili indeks pasaran saham AS, S&P500 dan Russell 2000, masing-masing.

Strategi ini secara amnya mewujudkan penyebaran antara pasangan ETF dengan panjang satu dan pendek jumlah yang lain. Nisbah panjang ke pendek boleh ditakrifkan dengan banyak cara seperti menggunakan teknik siri masa kointegrasi statistik. Dalam senario ini kita akan mengira nisbah lindung nilai antara SPY dan IWM melalui regresi linear bergulir. Ini kemudian akan membolehkan kita membuat penyebaran antara SPY dan IWM yang dinormalkan kepada z-skor. Isyarat perdagangan akan dihasilkan apabila z-skor melebihi ambang tertentu di bawah kepercayaan bahawa penyebaran akan kembali ke purata.

Rasional untuk strategi ini adalah bahawa SPY dan IWM kira-kira mencirikan situasi yang sama, ekonomi sekumpulan syarikat AS yang besar dan kecil. premisnya adalah bahawa jika seseorang mengambil penyebaran harga maka ia harus membalikkan purata, kerana sementara peristiwa lokal (dalam masa) boleh mempengaruhi sama ada indeks S & P500 atau Russell 2000 secara berasingan (seperti perbezaan modal kecil / modal besar, tarikh rebalancing atau perdagangan blok), siri harga jangka panjang kedua-duanya mungkin akan disatukan.

Strategi

Strategi ini dilaksanakan dalam langkah-langkah berikut:

1. Data - bar SPY dan IWM 1 minit diperolehi dari April 2007 hingga Februari 2014.
2. Pemprosesan - Data diselaraskan dengan betul dan bar yang hilang saling dibuang.
3. Spread - Nisbah lindung nilai antara kedua-dua ETF dikira dengan mengambil regresi linear bergulir. Ini ditakrifkan sebagai pekali regresi β menggunakan tetingkap kemunduran yang bergerak ke hadapan dengan 1 bar dan mengira semula pekali regresi. Oleh itu nisbah lindung nilai βi, untuk bar bi dikira merentasi titik bi−1−k ke bi−1 untuk kemunduran k bar.
4. Z-Score - Skor standard penyebaran dikira dengan cara biasa. Ini bermaksud mengurangkan purata (contoh) penyebaran dan membahagikan dengan penyimpangan standard (contoh) penyebaran. Alasan untuk ini adalah untuk membuat parameter ambang lebih mudah ditafsirkan kerana z-score adalah kuantiti tanpa dimensi. Saya sengaja memperkenalkan bias lookhead ke dalam pengiraan untuk menunjukkan betapa halusnya. Cuba dan berhati-hati!
5. Perdagangan - Isyarat panjang dihasilkan apabila z-score negatif jatuh di bawah ambang yang telah ditentukan (atau pasca optimum), sementara isyarat pendek adalah sebaliknya. Isyarat keluar dihasilkan apabila z-score mutlak jatuh di bawah ambang tambahan. Untuk strategi ini saya telah (agak sewenang-wenang) memilih ambang masuk mutlak z-score = 2 dan ambang keluar z-score = 1.

Mungkin cara terbaik untuk memahami strategi secara mendalam adalah untuk benar-benar melaksanakannya. Bahagian berikut menerangkan kod Python lengkap (fail tunggal) untuk melaksanakan strategi mean-reverting ini. Saya telah memberi komen secara liberal pada kod untuk membantu pemahaman.

Pelaksanaan Python

Seperti semua tutorial Python / pandas, anda perlu menyediakan persekitaran penyelidikan Python seperti yang dijelaskan dalam tutorial ini. Setelah dipasang, tugas pertama adalah untuk mengimport perpustakaan Python yang diperlukan.

Versi perpustakaan tertentu yang saya gunakan adalah seperti berikut:

• Python - 2.7.3
• NumPy - 1.8.0
• panda - 0.12.0
• Matplotlib - 1.1.0 Mari kita teruskan dan mengimport perpustakaan:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Fungsi berikut create_pairs_dataframe mengimport dua fail CSV yang mengandungi bar intraday dua simbol. Dalam kes kita ini akan menjadi SPY dan IWM. Ia kemudian membuat pasangan dataframe yang berasingan, yang menggunakan indeks kedua-dua fail asal. Oleh kerana cap masa mereka mungkin berbeza kerana perdagangan dan kesilapan yang terlepas, ini menjamin bahawa kita akan mempunyai data yang sepadan. Ini adalah salah satu faedah utama menggunakan perpustakaan analisis data seperti panda. Kod boilerplate dikendalikan untuk kita dengan cara yang sangat cekap.

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Langkah seterusnya adalah untuk menjalankan regresi linear bergulir antara SPY dan IWM. Dalam kes ini IWM adalah ramalan (x) dan SPY adalah tindak balas (y). Saya telah menetapkan tetingkap pandangan semula lalai 100 bar. Seperti yang dibincangkan di atas, ini adalah parameter strategi. Agar strategi dianggap kukuh, kita secara ideal ingin melihat profil pulangan (atau ukuran prestasi lain) sebagai fungsi melengkung tempoh pandangan. Oleh itu pada peringkat kemudian dalam kod, kita akan melakukan analisis kepekaan dengan mengubah tempoh pandangan kembali dalam julat.

Apabila pekali beta bergulir dikira dalam model regresi linear untuk SPY-IWM, kita menambahkannya ke pasangan DataFrame dan membuang baris kosong. Ini membentuk set bar pertama yang sama dengan saiz lookback sebagai ukuran pemangkasan. Kami kemudian membuat penyebaran kedua ETF sebagai unit SPY dan -βi unit IWM. Jelas ini bukan situasi yang realistik kerana kita mengambil jumlah pecahan IWM, yang tidak mungkin dalam pelaksanaan sebenar.

Akhirnya, kita membuat z-score penyebaran, yang dikira dengan mengurangkan purata penyebaran dan menormalkan dengan penyimpangan standard penyebaran. Perhatikan bahawa terdapat bias lookahead yang agak halus yang berlaku di sini. Saya sengaja meninggalkannya dalam kod kerana saya ingin menekankan betapa mudahnya membuat kesilapan seperti itu dalam penyelidikan. Purata dan penyimpangan standard dikira untuk keseluruhan siri masa penyebaran. Jika ini mencerminkan ketepatan sejarah yang benar maka maklumat ini tidak akan tersedia kerana secara tersirat menggunakan maklumat masa depan. Oleh itu, kita harus menggunakan purata bergulir dan stdev untuk mengira z-score.

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Dalam create_long_short_market_signals isyarat dagangan dicipta. Ini dikira dengan pergi panjang penyebaran apabila z-skor negatif melebihi z-skor negatif dan pergi pendek penyebaran apabila z-skor positif melebihi z-skor positif. Isyarat keluar diberikan apabila nilai mutlak z-skor adalah kurang daripada atau sama dengan ambang lain (lebih kecil dalam besar).

Untuk mencapai situasi ini adalah perlu untuk mengetahui, untuk setiap bar, sama ada strategi adalah in atau out pasaran. long_market dan short_market adalah dua pembolehubah yang ditakrifkan untuk mengesan kedudukan pasaran panjang dan pendek. Malangnya ini jauh lebih mudah untuk kod dalam cara berulang berbanding pendekatan vektor dan oleh itu ia lambat untuk mengira. Walaupun bar 1 minit memerlukan ~ 700,000 titik data setiap fail CSV ia masih agak cepat untuk mengira pada mesin desktop lama saya!

Untuk mengulangi di atas Pandas DataFrame (yang memang bukan operasi biasa) adalah perlu untuk menggunakan kaedah iterrows, yang menyediakan penjana di mana untuk mengulangi:

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

Pada peringkat ini, kita telah mengemas kini pasangan untuk mengandungi isyarat panjang / pendek yang sebenarnya, yang membolehkan kita menentukan sama ada kita perlu berada di pasaran. Sekarang kita perlu membuat portfolio untuk mengesan nilai pasaran kedudukan. Tugas pertama adalah untuk membuat lajur kedudukan yang menggabungkan isyarat panjang dan pendek. Ini akan mengandungi senarai elemen dari (1,0,−1), dengan 1 mewakili kedudukan panjang / pasaran, 0 mewakili tidak ada kedudukan (harus keluar) dan -1 mewakili kedudukan pendek / pasaran. Lajur sym1 dan sym2 mewakili nilai pasaran kedudukan SPY dan IWM pada akhir setiap bar.

Apabila nilai pasaran ETF telah dicipta, kita menjumlahkannya untuk menghasilkan nilai pasaran keseluruhan di akhir setiap bar. Ini kemudian diubah menjadi aliran pulangan oleh kaedah pct_change untuk objek Siri itu. Baris kod berikutnya membersihkan entri yang tidak baik (elemen NaN dan inf) dan akhirnya mengira kurva ekuiti penuh.

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Peraturanutamafungsi membawa semuanya bersama-sama. fail CSV intraday terletak di datadir laluan. Pastikan untuk mengubah suai kod di bawah untuk menunjuk ke direktori tertentu anda.

Untuk menentukan betapa sensitifnya strategi terhadap tempoh melihat kembali, adalah perlu untuk mengira metrik prestasi untuk julat melihat kembali. Saya telah memilih pulangan peratusan akhir portfolio sebagai ukuran prestasi dan julat melihat kembali di [50,200] dengan peningkatan 10. Anda boleh melihat dalam kod berikut bahawa fungsi sebelumnya dibungkus dalam gelung for merentasi julat ini, dengan ambang yang lain tetap. Tugas akhir adalah menggunakan matplotlib untuk membuat carta garis melihat kembali vs pulangan:

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

Jadual tempoh melihat balik vs pulangan kini boleh dilihat. Perhatikan bahawa terdapat maksimum 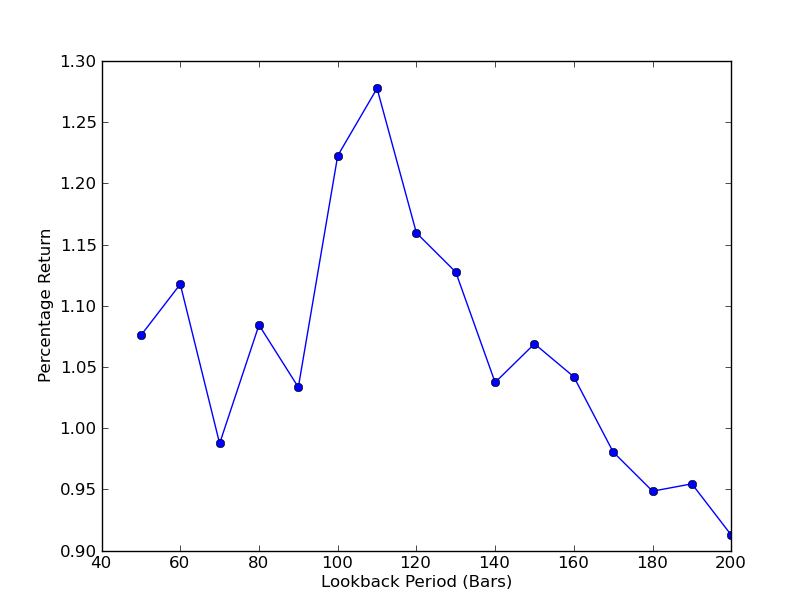global di sekitar melihat balik sama dengan 110 bar. Jika kita telah melihat situasi di mana melihat balik adalah bebas daripada pulangan ini akan menjadi penyebab kebimbangan:SPY-IWM analisis sensitiviti jangka masa jangkaan untuk nisbah lindung nilai regresi linear

Tiada artikel backtesting akan lengkap tanpa lengkung ekuiti yang miring ke atas! Oleh itu, jika anda ingin merangka lengkung pulangan kumulatif berbanding masa, anda boleh menggunakan kod berikut. Ia akan merangka portfolio akhir yang dihasilkan dari kajian parameter lookback. Oleh itu, perlu memilih lookback bergantung pada carta yang ingin anda lihat. Carta juga merangka pulangan SPY dalam tempoh yang sama untuk membantu perbandingan:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

Carta lengkung ekuiti berikut adalah untuk tempoh 100 hari: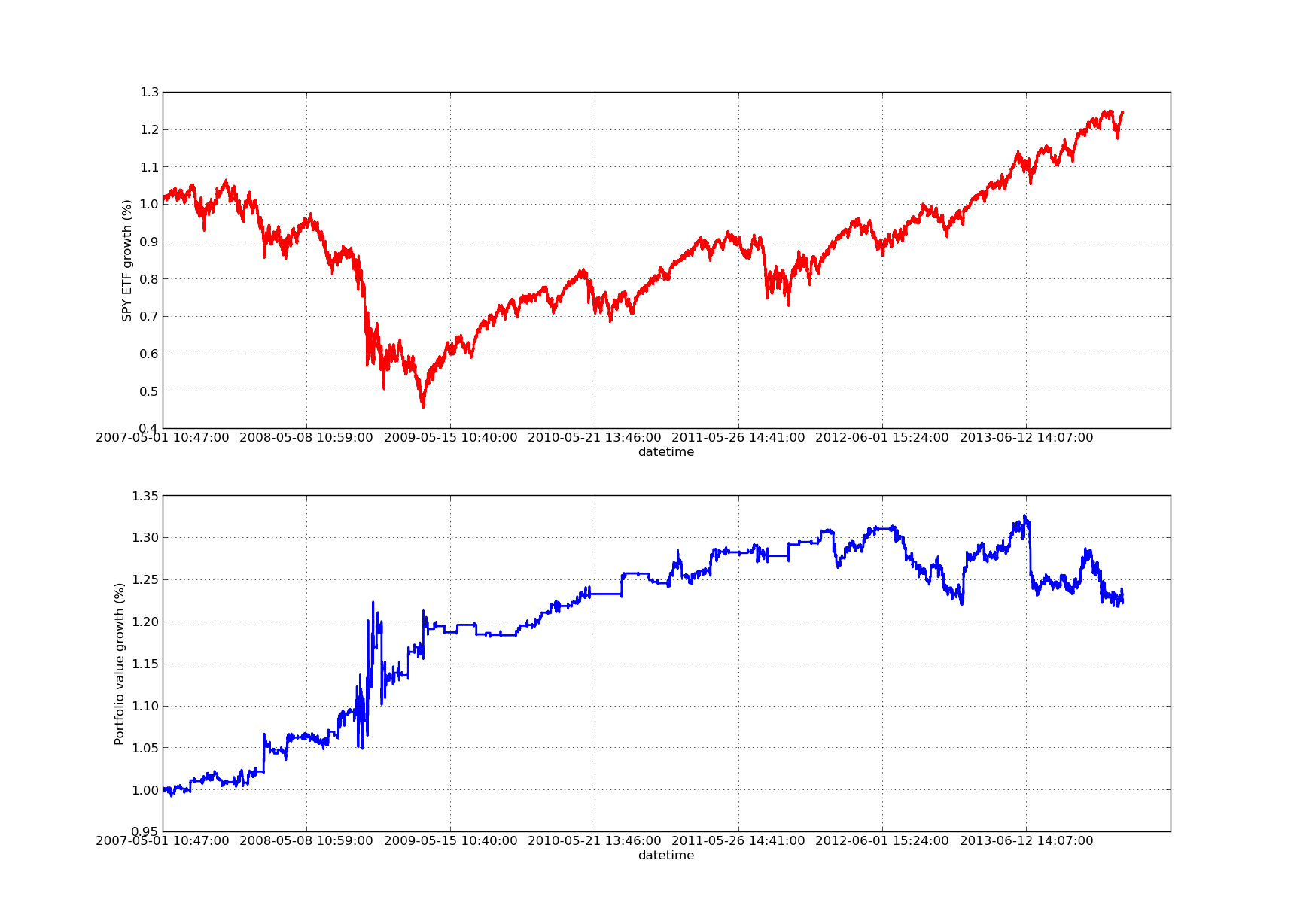SPY-IWM analisis sensitiviti jangka masa jangkaan untuk nisbah lindung nilai regresi linear

Perlu diperhatikan bahawa penggunaan SPY adalah ketara pada tahun 2009 semasa tempoh krisis kewangan. Strategi ini juga mengalami tempoh yang tidak menentu pada peringkat ini. Juga perlu diperhatikan bahawa prestasi telah merosot sedikit pada tahun lalu kerana sifat SPY yang kuat pada tempoh ini, yang mencerminkan indeks S & P500.

Perhatikan bahawa kita masih perlu mengambil kira kecenderungan lookahead ketika mengira z-score penyebaran. Selanjutnya, semua pengiraan ini telah dijalankan tanpa kos transaksi. Strategi ini pasti akan berfungsi dengan sangat buruk apabila faktor-faktor ini diambil kira. Yuran, penyebaran tawaran / permintaan dan seluncur kini tidak diperhitungkan. Di samping itu strategi ini berdagang dalam unit pecahan ETF, yang juga sangat tidak realistik.

Dalam artikel seterusnya kita akan mencipta backtester yang didorong oleh peristiwa yang lebih canggih yang akan mengambil faktor-faktor ini dan memberi kita keyakinan yang lebih besar dalam lengkung ekuiti dan metrik prestasi kita.